基于“一题一课”渐进式培养数学核心素养的教学实践

“一题一课”指通过对一道题（或一则学习材料）进行深入研究，对其所涉及的知识内容进行拓展延伸，挖掘其内在的学习资源与线索，由浅入深，由表及里，科学、合理、有序地组织和激励学生进行相关的数学探究活动，发展学生数学核心素养的一种教学模式。其有效实施的标准是教师对教学内容的有效整合、对学情的准确把握以及学生解决此类问题能力的提升。“一题一课”能够促进知识的即学即用，活学活用，减少基础薄弱学生的课堂学习负担，提升学生学习的自信心，从而为学生挑战其他高难度题型提供有效学习经验。下面，笔者以2024年江苏省苏州市中考数学的一道求线段最值试题为例，谈谈如何通过“一题一课”教学实践，培养学生的数学核心素养。

一、试题呈现

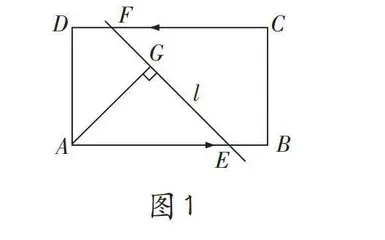
如图1，矩形ABCD中，AB=[√^-3] ，BC=1，动点E、F分别从点A、C同时出发，以每秒1个单位长度的速度沿AB、CD向终点B、D运动，过点E、F作直线l，过点A作直线l的垂线，垂足为G，则AG的最大值为（ ）。

二、教学实践

根据最近发展区理论，教师在选择题目时，要基于学生的现有水平，挑选那些略高于学生当前能力，但在教师引导和学生合作下能够解决的题目，因为这样的题目处于学生的最近发展区。动点最值问题是初中阶段最难、知识综合性最强、学生较畏惧的题型。关于此类问题，学生学过的知识有基本事实“两点之间线段最短”（点与点的距离）、“垂线段最短”（点与线的距离），遇到的题型有“将军饮马”“瓜豆原理”“胡不归”“一箭穿心”等。对于上述试题，教师可以引导学生从简单入手，从特殊入手，循序渐进，层层分析，逐步深入，以熟悉的题引向陌生的题，以易题引难题，通过“一题一课”，将“垂线段”在解决几何动点最值问题中的运用进行系统复习，帮助学生跨越最近发展区，发散思维，丰富思维涵养，实现数学能力的提升。

1.从基础入手，设计题型

在教学伊始，教师不妨先设计这样的问题：

如图2，AC=10，点B为平面内一动点，AB⊥BC，在点B运动的过程中，AB和BC的最大值是多少？

此题设计的目的是作为引子让学生回忆“两点之间线段最短”“垂线段最短”等基本事实。学生很容易知道，根据垂线段最短，在直角三角形中，直角边长度永远小于斜边长度。在点A到直线BC上任意一点的距离中，AB是最短的；在点C到直线AB上任意一点的距离中，BC是最短的。因此在点B运动的过程中，AB或BC的最大值为10，也就是点B与点C或点A重合时。

2.适当增加条件，继续设问，层层递进

在环节1的基础上，增加条件：

如图3，点C是线段AB的中点，直线l经过点C，点D、E是直线l上的点，AB=10，AD⊥DE，BE⊥DE，在直线l绕点C运动过程中，AD的最大值是多少？此时点E在什么位置？

学生根据环节1中问题的解决，会有意识地想到垂线段最短，可以很快判断，当点D运动到点C时，AD最大。此时点E也运动到了点C，直线l⊥AB。笔者教学时，一切从学情出发，以学生为主，通过对这两题的研究，勾起了学生对运用“垂线段最短”求最值问题的回忆，也加深了学生对其运用的意识以及对这类问题直观感知的敏锐度。

3.化繁为简，解决问题，增强信心

学生有了前面的探究，遇到一开始的中考试题，便有了直观经验，认为应该将AG放在一个斜边是定长的直角三角形中去考虑，自然就把AC连接起来，与EF相交于O点，如图4。因为DF=BE，所以CF=AE，易证△FOC[≅]△EOA，即AO=OC，当点G与点O重合时，AG最大，最大值就是AO的长。

通过这三道题目，学生既复习了垂线段最短，又增强了利用垂线段求最值的直观意识；既有能力提升，又有信心提振。探究到这里，教师不妨继续让学生提问题。学生在探究中继续发现，如图5，如果作CH⊥EF，那么当CH=CO时，CH最大，此时CH=AG，CH+AG的最大值也可以求出。

教育家夸美纽斯强调，教育要遵循自然秩序。他认为教学应该从易到难，从简单到复杂，从具体到抽象。就像大自然的万物生长都有其顺序一样，学生的学习过程也应该是循序渐进的。教师在教学中提供的简单任务应该处于学生的现有水平之上，但又不能超出他们的最近发展区。“一题一课”教学模式就是知识回忆与知识生成之间的桥梁，要让学生跳一跳，够得着。在教学过程中，学生通过对题目的不断思考、探索和交流，在已有知识经验的基础上，不断构建新的知识体系和解题思维模式。学生想跳想够着，“弹跳能力”自然就会提升。

4.试题训练，积累模型经验，强化直观素养

教师再给出一道题目，以强化学生的直观素养：

如图6，在△ABC中，∠C=60°，AC=5，BC=4，点D为CB延长线上一点。当点D在CB延长线上运动时，AD-[1/2]BD的最小值为_________________。

数学直观的前提是有必备的数学知识、模型和方法的储备，有生活与数学活动经验的积累，以及对研究对象的结构特征与关系的辨别能力。该问题是求线段之间的和差最值，题目中出现了[1/2]BD，运用转化思想，题目中有60[°]角，自然想到30[°]角所对直角边是斜边一半（使用三角函数），作∠C的平分线，构造30[°]角，再过点D作角平分线的垂线，如图7。学生通过构造“垂线段”模型，由陌生到熟悉，题目自然迎刃而解。

三、教学反思

《义务教育数学课程标准（2022年版）》强调，有效的教学活动是学生学和教师教的统一，学生是学习的主体；教学活动应注重启发式，激发学生学习兴趣，引发学生积极思考，鼓励学生质疑问难；促进学生理解和掌握数学的基础知识和基本技能，体会和运用数学的思想和方法，获得数学的基本活动经验。在实际教学过程中，许多教师喜欢设计题型多、容量大的课堂，满足于答案的呈现、任务的完成，不考虑学生的学情和学力，收效甚微。实践证明，讲多题不如深挖一题。本节课，笔者根据学情和学力，将一道题进行拓展延伸，巧妙设计，巧用变式，讲深讲透，促进了学生的推理能力、几何直观和模型观念的养成。对于“一题一课”课堂教学的实施，笔者认为应着重关注以下几点：

聚焦性。高度聚焦于一道题，所有教学活动围绕这一道题目展开，使教学目标明确且集中，避免教学内容的分散，让学生能够专注于核心问题的解决与思考。选材时，从学生熟悉的经历入手，尝试通过化特殊题型为一般路径去解决问题。在操作过程中，重视对思想方法的渗透，高阶思维的培养，思维品质的提升，引导学生积累数学活动经验，提高解决数学问题的迁移能力，拓宽视野，体会数学的价值，树立自信心，增强解题的决心和韧劲。

拓展性。从题目的条件、结论、解法等多个方面进行拓展延伸，深入浅出，有一定的知识容量，涉及多种数学思想方法，让学生思维得到真正的锻炼；问题具有层次性，改变题目中的条件，探究结论的变化，可以让不同学生在学力上得到不同的发展；问题具有开放性，即探究过程和结果是开放的，需要从不同的角度出发，寻求多种解题方法，以拓展学生的思维广度，让不同层次的学生都能参与其中；问题具有广延性，易于学生发现问题，进而做进一步的探究。

生成性。在课堂教学过程中，教师应鼓励学生积极参与讨论、探索，这样学生的观点和想法才会不断涌现，也会使得教学内容具有动态生成性。教师还要根据学生的反馈及时调整教学策略，以促进学生对知识的深入理解。

（作者单位：江苏省兴化市板桥初级中学）