以学生为中心，化抽象为具象

《义务教育数学课程标准（2022年版）》强调，有效的教学活动是学生学和教师教的统一，学生是学习的主体，教师是学习的组织者、引导者与合作者。数学教学从某种意义上说也是数学活动的教学。面对抽象的数学内容，教师要树立以学定教的理念，突出以学生为中心，基于学生的认知发展水平和已有经验，注重启发式教学和因材施教；发挥主导作用，处理好讲授与学生自主学习的关系，引导学生独立思考、主动探索、合作交流，使学生理解和掌握基本的数学知识与技能、数学思想和方法，获得基本的数学活动经验。下面，笔者以苏科版数学教材八（下）“6.1函数”的教学设计为例，谈谈以学生为中心的具体教学实践。

一、教学目标

通过简单实例，了解常量与变量的意义；通过实例，多角度、多层面地认识和理解函数的意义，感受函数的多种表示形式；能说出一些关于函数的实例，并能判断两个变量间的关系是不是函数关系；在互动探究和问题解决中体会函数是研究两个变量之间关系的重要模型。

二、教学过程

1.情境引学：初步感悟生活中的变化

师：同学们，变化让我们的生活多姿多彩。随着四季的变化，气温也随之变化；随着年龄的增长，大家的个子越来越高……变化也时常给我们带来困惑，引领我们探究新知。这堂课就让我们一起去探究吧。

教师展示与生活相关的图片，如心电图、气温变化的图片、铅球抛掷后的轨迹图等。

【设计意图】 由学生熟悉的话题引入，学生在观察气温变化等的动态过程中，感悟变化。

2.互动研学：研究变量关系

（1）初步感悟生活中的常量与变量。

师：请大家观察，列车在匀速行驶的过程中，涉及哪些量呢？在这些量中，有哪些量是没有变化的，哪些量是不断变化的？

学生一起回答。教师及时板书。板书时，速度写一栏，路程和时间各写一栏。

师再举例：每支铅笔2元，买了a支铅笔用了b元；每小时加工5件零件，x小时加工了y件零件。

师：在这两个问题中，哪些是不变的量，哪些是变化的量？你知道是怎么变化的吗？

学生讨论后回答。

师：你还能举出生活中的某些变化过程并说明其中哪些是不变的量，哪些是变化的量吗？

学生热烈讨论。师生归纳出两个新的概念，即常量与变量的概念。

【设计意图】 由“变”到“变化的量”，实现从生活到数学的自然过渡。学生亲身经历“提出问题→寻找其中的量→对量进行分类→归纳概念”的过程，感受数学概念形成的自然性与合理性。

（2）研究变量关系。

师：由于常量始终保持不变，所以我们重点研究变量，在不同的变化过程中探索变量与变量之间的关系。

引例：在列车行驶过程中，有哪些变量？有哪些常量？

学生异口同声回答：速度是常量，路程和时间是变量。

师：同学们，听清我的问题哦，我这里有没有说列车是匀速行驶的呢？

学生独立思考，交流。

生1：列车有可能是匀速行驶的，那么速度就是常量，路程会随着时间变化而变化。也有可能速度是变化的，路程、时间和速度都是变量。

师：非常好。那大家再试想一下，假设你从徐州坐列车到上海，在这个过程中，列车速度变化吗？

学生异口同声回答：变化。

师：那路程呢？

生2：路程是常量。

师：所以，在一个变化过程中，常量和变量不是绝对的，而是相对的。假设列车匀速行驶，当时间取一个值时，路程有几个值？

生3：根据路程=速度×时间，速度确定时，路程只有一个值。

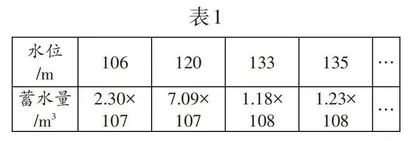
问题1：已知水库的水位变化与蓄水量变化情况如下表所示。

师：表1中有几个变量？这些变量之间有什么关系？

生4：有两个变量，分别是水位和蓄水量。当水位取一个值时，蓄水量也有一个值与它对应。

师追问：蓄水量是唯一的吗？

生4：是的。

师：我们把答案再组织完整，对于水位的每一个值，蓄水量都有唯一的值与它对应。

学生复述一遍，加深印象。

问题2：你去过游乐园吗？你坐过摩天轮吗？你能描述一下坐摩天轮的感觉吗？

师追问：人坐在摩天轮上，人的高度随时间的变化而变化。那么这种变化有规律吗？假设摩天轮上一点的高度h（m）与旋转时间t（min）之间有一定的关系，如图1，你能从图像上观察出有几个变量吗？当时间取一个值的时候，相应的高度是多少？给定一个t的值，你能找到相应的h值吗？

学生热烈讨论，积极性极高。

生5：我坐摩天轮时很害怕，因为我恐高……

师追问：能再具体描述一下吗？

生5：我从摩天轮最低点进舱，然后摩天轮越转越高，最后到最高点，然后慢慢再下降。

师追问：在旋转的过程中，你能发现哪些变量？注意回答的准确性。

生5：我能发现两个变量。摩天轮的高度和旋转时间是变量，当时间取一个值时，高度有唯一一个值与时间对应。

师：回答得非常好，语言清晰准确，请大家给他鼓鼓掌，希望他能克服恐高的弱点，更加睿智和勇敢。

师生热烈鼓掌，课堂氛围浓厚。

问题3：图2是宿迁某一天的气温变化曲线图。

师：根据前两个问题的经验，尝试提出问题并解决问题。

生6：在这个变化过程中有几个变量？变量之间有什么样的关系？

……

师生讨论。

【设计意图】 让学生进一步感悟变化过程中的变量与常量、两个变量的对应关系，引导学生多方面思考问题，防止学生形成思维定式；培养学生自主思考的能力，引导学生发现问题的关联性和普遍性，体会函数的对应关系。

3.探究深学：抽象并建构函数概念

师：同学们请思考，这三个问题有什么共同之处呢？

学生相互讨论、总结：每个变化过程都有两个变量，且当其中一个变量变化时，另一个变量也随之变化；当其中一个变量确定时，另一个变量也随之确定。

师生归纳函数的定义。随后，教师渗透与函数相关的数学史，接着，再带领学生“回头看”。

师：对于前面的实例，现在可以用函数的思想来理解两个变量之间的关系。说一说上面三个问题中，谁是谁的函数？

【设计意图】 由于学生首次接触函数概念，因此在学习中重在让学生感受概念。通过大量的具体事例，学生充分认识事物的变化过程，探索在这个变化过程中两个变量之间的相互关系，提升认识，建构函数概念。

4.反馈悟学：迁移运用

理解应用：判断两个变量之间的关系是不是函数关系。

（1）判断年份与身高是不是函数关系。

生7：身高是年份的函数。因为当年份取一个值时，身高有唯一一个值与它对应。

师追问：还有其他的想法吗？

学生沉思，回答：年份可不可以是身高的函数？

师：非常好。对于这个问题，有没有哪位同学能回答出来呢？

学生疑惑皱眉，沉思静默，随后积极交流。教师列表2帮助学生理解。

生8：身高不是年份的函数。因为到了2022年以后，身高是166cm，当身高取166cm时，年份有2022、2023等，年份不是唯一的值与身高对应，所以身高不是年份的函数。

师：大家同意他的说法吗？

学生回答同意，仍有部分学生未理解。教师组织学生交流讨论并选小组代表展示想法。

（2）下面变化关系中，y是x的函数吗？

①y=[x]；②[y]=x。

（3）科学研究表明，人在运动时的心跳速度通常与年龄有关，一个人在运动时所承受的每分钟心跳的最高次数（b次）随着个人的年龄（a岁）变化而变化的规律为：b=-0.8a+175.8。这个问题中有几个变量？哪几个量是自变量？哪个是函数，为什么？正常情况下，一个12岁的少年在运动时所能承受的每分钟心跳的最高次数是多少？一个50岁的人在运动时1分钟内心跳次数为150次，他有危险吗？

【设计意图】 给学生一种思考的方法，即“回到定义去”，强调用函数的定义来思考；强化学生对一一对应关系的理解。

5.回顾思学：归纳小结（略）

三、教学反思

课堂目标以学生为中心。“让学生学会什么”是教师心中要时刻装着的目标。课堂所有的活动都围绕达成目标而设计，要删减无效活动。教师在每节课中的成长目标也要具体而清晰，并且集中在某些点上，长此以往，教师的成长也会是明显的。

课堂活动以学生为中心。现在课堂上仍然存在教师与学生一问一答的现象，虽然是不同的学生在回答问题，但是本质上与一问一答并没有太大区别。为避免这种现象发生，笔者采用思考、分组、分享的形式，给学生独立思考的时间，先让学生和同伴分享想法，再在班级分享；让每个学生都有发声的机会，都动脑思考，将注意力集中到问题上去，进而学会本节课的内容，达成本节课的目标。

课堂引导以学生为中心。课堂引导用语是教师向学生解释课堂要求、课堂流程、课堂活动规则等的语言。课堂引导应从学生角度出发，转换说法，以简单清晰的语言传达给学生，让学生能够用最短的时间接受并执行。因此教师要用心设计，减少讲解时间，缩短指令用语，避免解释过多而导致学生产生更多困惑。可以以多种方式了解学生是否听懂指令，如随机询问、举例示范等。

以学生为中心的课堂，并不是看上去学生在很热闹地讨论，或者看似每个人都有一次表达或展示的机会，这仅仅是浅显的全员参与。课堂该放手时就放手。实现以学生为课堂中心的目标任重道远，从知识传承到全面育人，需要不断磨砺和创新。

（作者单位：江苏省宿迁市宿城区新区初级中学）