基于OBE教育理念的高等概率论课程改革与创新

摘要：高等概率论作为数学统计学专业的重要课程，具有理论性强、内容抽象等特点。在教学过程中，该课程存在理论抽象难理解、教学方式单一、学生参与度低等问题。针对这些问题，文章基于OBE教育理念，从明确学习成果、优化课程体系、实施有效的教学策略、完善评价体系、持续改进与反馈五个方面进行改革与创新。

关键词：OBE；高等概率论；案例

OBE（成果导向教育）是一种以学生学习成果为导向的教育理念。它强调从预期的学习结果出发，逆向设计教学过程，确保所有学生都能达到预定的学习目标。

一、明确学习成果目标

高等概率论课程（以下简称课程）以培养具有扎实统计学学科基础理论和专门知识，能利用统计方法解决实际问题的高级专业人才为目标。通过课程的学习，学生可以系统地了解概率论的基本知识，掌握测度论、高等概率论相关理论中的基本方法和基本技巧，为学生深入学习随机过程、随机分析和数理统计等奠定基础，并培养学生抽象思维。通过对概率论中若干重要定理的推理，学生能提高严谨的逻辑能力和科学精神。

二、优化课程体系

（一）引入实际案例

在教学中，教师可以适时引入与专业相关，与科技前沿、时事热点相关的应用案例及课程思政案例，引导学生用概率论的思想、方法将其转化为数学问题，并采用恰当的数学方法求解。

1.案例一：乘积空间上的测度与积分

在数学分析中，低维空间与高维空间的表示法、体积与积分之间的关系，以及重积分化为累次积分等问题都是非常重要。因此，讨论抽象空间中的这些问题具有重要意义，即如何由“低维”可测空间及其测度构造“高维”可测空间及其测度；如何由“重积分”化“累次积分”以及如何构造任意多个概率空间的乘积概率空间的问题。

乘积空间上的测度与积分理论在数学及其他科学领域中有着广泛的应用。例如，在统计学中，特别是多元统计分析中，经常需要处理多个变量的联合分布，乘积空间上的测度与积分理论提供了处理这类问题的工具，有助于理解变量间的相关性和依赖性；在量子力学中，状态空间通常是一个希尔伯特空间，而多个粒子系统的状态位于这些空间的张量积上，因此乘积空间上的测度和积分理论对于理解与计算多粒子系统的行为至关重要。在机器学习和人工智能领域，特别是在处理多维数据或特征时，乘积空间上的测度和积分理论可以用来定义与优化模型，尤其是在贝叶斯网络中，节点之间的概率关系可以用乘积空间上的测度来表示，从而帮助进行推理和预测。

2.案例二：Radon-Nikodym定理的证明及其应用

首先，教师直观地介绍Radon-Nikodym定理（拉东-尼克蒂姆定理）的内容。在可测空间上，如果有一个符号测度和一个有限测度，且符号测度关于测度绝对连续，则在几乎处处相等的意义下存在唯一的Borel可测函数（波莱尔可测函数）使之成为符号测度关于该有限测度的Radon-Nikodym导数。该定理结论中“存在性”的证明，采用“从特殊到一般”的证明思路，这种证明方法在数学定理的证明过程中特别经典，非常具有代表性。教师通过逐步分析该定理的证明思路，可以强化学生的逻辑推理能力，进而增强学生解决一般数学问题的科学思维。

Radon-Nikodym定理是测度论中的一个基本结果，它提供了两个测度之间关系的一种描述方式。该定理虽然内容比较抽象，但在概率论、统计学、经济学、金融数学等领域有着广泛的应用。例如，在统计推断中，Radon-Nikodym定理用于比较不同假设下的似然函数，尤其是在假设检验中，可以通过计算两个假设下观测数据的Radon-Nikodym导数来决定哪个假设更合理；在贝叶斯统计中，先验分布和后验分布之间的关系可以通过Radon-Nikodym导数来表达；在金融数学中，Radon-Nikodym定理用于定义等价鞅测度，这是无套利定价理论的核心，通过找到一个关于物理测度绝对连续的风险中性测度，可以将衍生品的价格表示为在风险中性测度下的期望值；在信息论中，Radon-Nikodym定理用于定义Kullback-Leibler散度（又称为相对熵），这是衡量两个概率分布之间差异的一个重要指标，而相对熵的定义涉及两个概率测度之间的Radon-Nikodym导数。

（二）增加实践环节

MATLAB（矩阵实验室）、Mathematica（科学计算软件）、Maple（数学家的软件）并称为三大数学软件，在数学类科技应用软件中在数值计算方面首屈一指。借助数学软件，学生可以更好地理解和掌握所学内容。学生可以运用数学软件完成关于条件概率、期望、零一律、中心极限定理、大数定律等内容的随机数模拟，学生应用数学软件实现随机现象的图像和试验，提高动手能力和创新实践能力；理论加实践的教学方法在保证学生学好理论知识的同时，培养了学生运用数学软件解决问题的兴趣和能力，进而提高学生在数学建模竞赛等赛事中的获奖率。

三、实施有效的教学策略

（一）强调理论与实践相结合

对于想继续深造的学生，教师应加强理论深度，提供前沿的研究课题和学术讨论的机会。例如，在讲授条件期望相关章节时，教师可以介绍Markov过程（马尔可夫过程）和鞅过程的定义，并用两者的定义，判断某些随机过程是否具有Markov性质或鞅性质。同时，高等概率论课程中有很多定理都是以早期国外概率学家的名字命名的，如Fubini定理（富比尼定理）、Kolmogorov零一律（柯尔莫哥洛夫零一律）等，容易让学生产生国内缺少从事概率论研究的数学家或者我国概率论研究不强的错觉。实际上，中国在概率论及相关领域涌现了许多杰出的数学家和概率学家，他们在国际上享有很高的声誉，并取得了许多世界一流的成就。

例如，中国科学院院士王梓坤主要从事概率论和随机过程的研究，他在随机过程的极限理论、随机微分方程及随机动力系统等方面作出了重要贡献。王梓坤的工作在国际上得到了广泛认可，他的研究成果被应用于多个领域，包括金融数学和生物统计学；中国科学院院士彭实戈主要从事概率论和金融数学的研究，他是中国金融数学的奠基人之一，特别是在倒向随机微分方程（BSDE）和非线性期望理论方面作出了开创性的贡献。彭实戈的工作在国际上得到了广泛认可，他的研究成果对金融市场的风险管理、资产定价等领域产生了重要影响。教师可以进一步介绍我国概率学家如王梓坤院士、彭实戈院士等专家学者在Markov过程、正倒向随机微分方程等领域内的杰出成就，激发学生继续深造的兴趣。

（二）个性化辅导

根据学生的不同职业目标，教师应开展个性化的指导。例如，对想要考公务员的学生，教师应指导他们理解如何在逻辑推理部分运用概率知识；对希望从事研究工作的学生，教师应引导他们参与科研项目；对想进入中学任职的学生，教师可以通过案例分析、实际问题解决等方法，将复杂的概率论概念简化，并联系到基础教育中的数学内容。例如，高等概率论课程中涉及一些重要定理的证明，而证明思路是中学阶段就学习和使用过的反证法、数学归纳法等，教师通过分析这些方法的精妙之处，可以帮助将来想从事教育行业的学生强化数学思维，进而提高教学水平。

（三）促进交流与合作学习

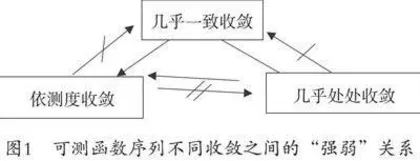
通过课堂讨论、辩论赛或者模拟授课等活动，学生会互相学习对方的观点和想法，同时锻炼表达能力和团队协作能力。例如，对可测函数序列几种收敛之间的“强弱”关系（如图1所示），在学生学习了“强”收敛能推出“弱”收敛的证明之后，教师可以引导学生独立思考或小组讨论：为什么“弱”收敛不能推出“强”收敛，且给出“弱”收敛不能推出“强”收敛的例子，最后让学生讲出相关反例。

（四）利用技术辅助教学

教师使用在线资源如视频讲座、虚拟实验室等工具来丰富课程内容，使抽象的概率论概念更加直观易懂。例如，利用学习通，建立线上课程，教师可以在章节内发布速课视频，在资料文件夹中分享课件和相关领域的前沿问题的学术论文，还可以鼓励学生在班级空间内畅所欲言，方便学生随时提问和分享资料。

四、完善评价体系

目前单一的期末闭卷考核已经不能充分反映学生对课程内容的掌握程度，所以教师要优化考核方式，将章节测试、课堂报告和小论文等环节纳入平时作业的考核内容，并按照平时作业15%+课堂表现10%+章节测试15%+期末考试60%的分配额度进行考核，考试实行考教分离制度，试题的选取要求易、中、难的比例为3∶5∶2，这样的考核制度能更好地检验学生对理论知识的理解能力和证明计算能力，实现课程知识目标、能力目标和育人目标的结合，提高人才培养质量。

五、持续改进与反馈

教师收集来自学生和其他同行教师听课的反馈，并且定期审查课程的有效性，并根据学生和同行教师的意见和建议做出必要的调整。在师生互动方面，教师坚持开放式交流，创建一个积极互动的学习环境。教师扮演引导者的角色，帮助学生识别他们的优势领域，从而更有效地达成学习成果。例如，中国矿业大学（北京）每学期都会有督导组专家教师进课堂听课，课后专家会针对课堂师生表现给出具体的意见和建议。根据这些宝贵的意见和建议，教师认真反思和重构教学环节，不断优化教学策略，提高学生在课堂内外的学习效率。此外，教师应坚持参加科研、教学活动，保持课程内容与时俱进。

综上所述，基于OBE教育理念，在高等概率论的教学过程中，教师可以创造一个更加以学生为中心、注重实效的教学环境，不仅能提高教学质量，也能更好地满足学生未来职业生涯的需求。

参考文献：

[1]李红，陈亮，张自武，等.OBE理念下“概率论与数理统计”课程目标达成度评价研究[J].西部素质教育，2024（19）.

[2]刘小云，郭艳冬.OBE教育理念下概率论与数理统计教学评价机制实践研究[J].创新创业理论研究与实践，2024（8）.

[3]赵鲁涛，张志刚.“学以致用，以用促学”创新高校课堂教学[J].中国高等教育，2015（17）.

[4]朱亚茹，史会峰，田景峰.“以产出为导向”的概率论与数理统计教学探索与实践[J].科教导刊，2021（25）.

[5]陈睿涵.概率论在实际生活中的应用和拓展[J].科学技术创新，2020（3）.

[6]唐琳.中国概率学家的成就与情怀：概率论领域马志明、严加安侧记[J].科学新闻，2015（12）.

[7]王梓坤.科学发现纵横谈[M].北京：北京师范大学出版社，2009.

基金项目：中国矿业大学（北京）2024年研究生教育教学改革项目“高等概率论课程的改革与创新探究”，项目编号：YJG2024018。