基于中华优秀传统文化视角的小学数学单元整体教学研究

［摘 要］在小学数学教学中融入中华优秀传统文化是发展学生数学核心素养的重要途径之一，也是素养导向下单元整体教学实施的有效支点。文章立足整体视角，遵循学生的认知发展规律，整合单元内容和文化素材，制订基于中华优秀传统文化的单元目标，设计融入中华优秀传统文化的学习任务，研制“数学+文化”的多元评价量表，帮助学生理解知识本质，感悟数学精神，增强文化自信，发挥中华优秀传统文化和数学学科的育人价值。

［关键词］中华优秀传统文化；圆；单元教学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）11-0041-04

随着《中华优秀传统文化进中小学课程教材指南》的颁布和《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）提出的“关注数学学科发展前沿与数学文化，继承和弘扬中华优秀传统文化”，越来越多的中华优秀传统文化进入小学课堂。数学教育承载着落实立德树人的根本任务，在小学数学教学中融入中华优秀传统文化，能帮助学生理解中华优秀传统文化中的数学智慧，感悟数学思想，继承数学精神，增强文化自信，发挥中华优秀传统文化和数学学科的育人价值。

一、内涵叩问

中华优秀传统文化内涵丰富，传统建筑、民间艺术、数学典籍、数学家的故事等都可以为小学数学教学提供学习素材。学生通过探究其蕴含的数学原理，经历数学知识发展的脉络，能感受中华优秀传统文化的博大精深，体会古人的杰出智慧，从而增强民族自信心和自豪感。

《课程标准》提出，单元整体教学设计要整体分析数学内容本质和学生的认知规律，合理整合教学内容，分析主题—单元—课时的数学知识和核心素养主要表现，确定单元教学目标，并落实到教学活动各环节，整体设计，分步实施，促进学生对数学教学内容的整体理解与把握，逐步培养学生的核心素养。

基于中华优秀传统文化视角的小学数学单元整体教学是指以数学知识的逻辑结构和学生的认知水平为基础，将教材内容和文化素材进行结构化整合，制订基于中华优秀传统文化的单元目标，设计融入中华优秀传统文化的学习任务，研制“数学+文化”的多元化评价量表，在教学中发展学生的数学核心素养，增强学生的文化自信。

二、价值探寻

（一）启智增慧，理解知识本质

教师从数学知识的逻辑顺序、学生的认知水平以及传统文化的发展脉络等方面入手，立足单元整体，整合单元内容和小学数学教材中的文化元素，引导学生经历“再创造”的过程，了解数学知识的产生、发展过程，使其自主探索新知，深入理解知识本质，从而建构数学知识体系。

（二）以文化人，感悟数学精神

将中华优秀传统文化与小学数学教学进行融合是落实立德树人根本任务的重要路径之一。学生通过探究自然现象或现实情境背后的数学原理，经历数学知识“再发现”的过程，既可以体会数学思想，学习数学家锲而不舍的钻研态度和勇于探索的科学精神，又可以提高动手操作能力，感受数学与生活的联系，体会数学之美。

（三）以文立心，增强文化自信

中华优秀传统文化为小学数学教学提供了积极向上的价值导向和文化精神，学生在掌握数学知识的同时感受中华优秀传统文化的审美价值和实践价值，有助于发展自身的数学核心素养和文化修养，增强文化意识和民族自豪感，提升自身的文化认同感。

三、路径实施

在单元整体教学中融入中华优秀传统文化，发挥中华优秀传统文化的育人价值，是小学数学教学的重要课题之一。下面，笔者以苏教版教材五年级下册的“圆”单元为例展开论述。

（一）制订基于中华优秀传统文化的单元目标

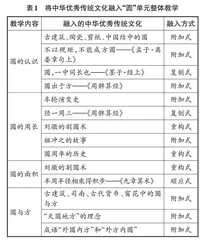
汪晓勤教授将中华优秀传统文化融入数学教学的方式分为附加式、复制式、顺应式和重构式。根据这一观点，笔者充分挖掘单元内容中蕴含的文化元素，对中华优秀传统文化融入“圆”单元整体教学的内容与方式进行了梳理与汇总（见表1）。

结合《课程标准》要求、不同版本教材内容的异同以及“圆”单元中蕴含的文化元素，笔者制订了基于中华优秀传统文化的单元目标。

【目标1】在观察、画图、测量等活动中认识圆和扇形的特征；会用圆规画圆；会运用圆的知识解释生活中的圆。

【目标2】推导圆的周长和面积的计算方法，积累活动经验，感悟转化思想、极限思想等，形成量感，增强空间观念和推理意识，发展几何直观。

【目标3】了解圆周率的历史，讲述刘徽和祖冲之的故事，感受中华优秀传统文化与数学的联系，体会数学家勇于探索的科学精神，增强文化自信。

（二）分析学习起点

根据皮亚杰的认知发展理论，小学高年段学生的思维发展水平正由具体形象思维向抽象逻辑思维过渡。学生在一年级已经直观认识了圆；在三年级学过用“绕绳法”测量树叶的周长，初步体会“化曲为直”思想；在五年级上学期运用转化思想推导多边形的面积公式。这些内容的学习为研究圆的特征、周长和面积奠定了基础。“圆”的内容被编排在五年级下学期，符合学生的认知发展规律。

通过与学生交谈，笔者了解到学生在生活中已经积累了大量关于圆的生活经验，但大部分学生只会借助实物画圆。由于圆心和半径无法直接观察，学生对圆的本质特征没有清晰的认识，而且研究圆的周长和面积的方法也与研究其他平面图形不同。因此，这一内容对于学生来说相对抽象。

（三）设计融入中华优秀传统文化的学习任务

根据单元目标和学生的学习起点，笔者从中华优秀传统文化和单元整体教学的双重视角出发，对“圆”单元内容进行调整与优化（见表2）。

由于圆与方的关系和转化思想是“圆”单元的教学主线，因此“圆”单元有四节核心课——圆的认识、探究圆的周长、探究圆的面积、圆与方。

1.种子课：圆的认识——理解“一中同长”和“圆出于方”

【任务1】通过实物认识圆，初步感知“一中同长”。先引入生活中的圆，再让学生欣赏古建筑、陶瓷、剪纸、中国结中的圆，体会圆与中华优秀传统文化之间的联系。学生在思考“圆和以前学过的其他平面图形有什么不同”的过程中体会圆的曲线美。

【任务2】在画圆活动中体会“一中同长”。环节1：自主选择身边的物体来画圆。学生借助生活中的实物（如胶带、瓶盖、圆片等），沿着实物的边缘拓印出圆。环节2：用圆规画圆。通过《孟子·离娄章句上》中的“不以规矩，不能成方圆”引导学生用圆规画圆，并讨论“用圆规画圆和借助其他实物画圆有什么不同”，从而认识圆的特征。

【任务3】在中华优秀传统文化中理解“一中同长”。通过出示《墨子·经上》记载的“圆，一中同长也”，讨论“一中”和“同长”的含义，发现古人用精准简短的语言概括出圆的特征，体会数学的简洁美。

【任务4】在动手操作中深化“一中同长”。通过折一折、画一画、比一比等方法验证“一中同长”，发现圆是轴对称图形，感受圆的对称美。

【任务5】在对比中感知“圆出于方”。通过学习《周髀算经》中的“圆出于方”，体会圆与正方形（正多边形）的关系，为后续运用“化圆为方”思想学习圆的周长和面积作铺垫。

2.活动课：探究圆的周长——体会“化曲为直”思想

【任务1】情境引入，初步感知。通过微视频出示车轮演变史以及车轮滚动一周的路程引入“周长”，引导学生初步感知圆的周长与其直径有关。

【任务2】观察猜想，区间逼近。可将任务细分为3个驱动性活动——（1）算一算：正方形、圆形和正六边形的组合图形中（如图1），哪个图形的周长最长？哪个图形的周长最短？（2）想一想：正方形的周长是圆直径的几倍？六边形的周长是圆直径的几倍？（3）估一估：圆的周长大约是其直径的几倍？学生在探究中发现圆的周长大约是其直径的3倍，体会到圆与方之间的联系，既与前面的“圆出于方”相呼应，又与后面“化圆为方”和“圆与方”互相转化奠定基础。

【任务3】化曲为直，操作验证。运用“绕绳法”“滚动法”或“软尺法”测量圆的周长，验证圆的周长大约是其直径的3倍，体会“化曲为直”思想。

【任务4】融入数学史，认识圆周率。通过学习圆周率的历史，学生发现自己计算得出的结论与《周髀算经》记载的“径一周三”很接近，从而激发学习兴趣，增强文化认同感。通过讲述刘徽的割圆术和祖冲之的故事，体会中国古代数学家勇于探索、大胆创新的科学精神。

【任务5】推导公式，深化应用。根据“圆的周长÷直径=圆周率”倒推圆的周长，培养逆向思维。

3.活动课：探究圆的面积——感悟“化圆为方”思想和“无限趋近”的极限思想

【任务1】复习导入，渗透转化思想。复习求多边形面积的方法（数方格和转化），并将两种方法迁移到求圆的面积的过程中。在这个过程中，学生发现数方格的方法不够准确，从而激发求知欲，产生转化图形的需求。

【任务2】操作想象，感悟极限思想。可将任务细分为3个驱动性活动——（1）思考：可以将圆转化成以前学过的什么平面图形？怎样转化？（2）操作：沿着圆的直径将圆平均分成4份，可以近似拼成以前学过的什么图形？平均分成8份、16份，可以近似拼成什么图形？（3）想象：如果将圆平均分成32份、64份……无限平均分割下去，拼成的图形会是什么？学生在操作和想象中理解将圆平均分成若干份可以拼成长方形，体会“化圆为方”思想和“无限趋近”的极限思想。

【任务3】动画演示，推导圆的面积公式。通过几何画板动画演示圆被分成若干份，再拼成长方形的过程，引导学生思考“拼成的长方形与原来的圆有什么关系”。学生在讨论中发现转化前后图形的面积不变，圆的半径变成了长方形的宽，圆周长的一半变成了长方形的长，感悟“等积变形”和“变与不变”的数学思想。

【任务4】融入数学史，了解圆面积的多种计算方法。通过微视频介绍刘徽的割圆术，让学生“重走”数学家的研究之路，进一步感受极限思想。出示《九章算术》丈量土地的经典数学题，引导学生发现用圆周长的一半乘半径可以得到圆的面积，这与《九章算术》中记载的“半周半径相乘得积步”方法一致。学生在了解古代经典数学著作的同时，灵活运用圆的知识解决实际问题，既发展了解题能力，又增强了文化认同感。

4.拓展课：圆与方——运用转化思想解决问题

【任务1】文化引入，初步感知。通过古建筑、司南、古代货币、窗花中的圆与方，介绍古代“天圆地方”的寓意，引出“圆与方”的面积问题，激发学生的学习兴趣，调动学生的学习积极性。

【任务2】探究“外方内圆”（如图2-1）。通过观察发现圆外切正方形的边长与圆的直径长度相等，从而很快计算出正方形和圆的面积。

【任务3】探究“外圆内方”（如图2-2）。学生在探究过程中发现正方形的边长未知，需要将正方形分成2个三角形，这样求正方形的面积就转化成求2个三角形的面积，每个三角形的底相当于圆的直径，高相当于圆的半径。学生在解决问题过程中体会到“圆”与“方”可以互相转化。

【任务4】发现一般规律。该任务可以设置3个驱动性问题——（1）圆形（半径为r）和正方形的组合图形（如图2-1、图2-2）中，每个图形中的圆形与正方形的面积分别是多少？（2）每个图形中，圆形与正方形的面积分别与圆的半径有什么关系？（3）每个图形中，圆形与正方形非重合部分的面积与圆的半径有什么关系？通过这些问题引导学生经历解决问题的全过程，总结一般结论，为研究“圆与方”的变式问题扫清认知障碍。

【任务5】介绍成语，渗透文化。通过介绍“外方内圆”和“外圆内方”两个成语的含义，体会中华优秀传统文化的博大精深。

（四）研制“数学+文化”的多元评价量表

《课程标准》提倡“教—学—评”一致性，注重多元维度评价和多样主体评价。对此，笔者依据单元目标研制了“数学+文化”的多元评价量表（见表3），以了解学生的学习情况。

综上所述，在小学数学教学中融入中华优秀传统文化是发展学生数学核心素养的重要途径之一，也是素养导向下实施单元整体教学的有效支点。在实际教学中，教师应立足整体视角，遵循学生的认知发展规律，整合单元内容和文化素材，帮助学生把握知识发展的脉络，深度理解数学知识，感悟数学精神，增强文化自信，发挥中华优秀传统文化和数学学科的育人价值。

［ 参 考 文 献 ］

[1] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2] 刘婷，于海杰，吴广莹，等.小学数学不同版本“圆”单元教学内容的比较研究：以人教版、北师大版和苏教版教材为例[J］.赤峰学院学报（自然科学版），2024，40（4）：113-118.

[3] 汪晓勤.HPM：数学史与数学教育[M].北京：科学出版社，2017.

【本文系江苏省教育科学“十四五”规划2024年度课题“全景式浸润：小学数学文化实践活动的构建与实施”（编号：C/2024/03/39）阶段性研究成果。】

（责编    覃小慧）