指向深度学习的任务驱动教学策略探索

［摘 要］深度学习是在教师适度引导下，学生围绕具有挑战性的学习内容，积极参与，获得发展的有意义的学习过程。任务驱动是学生在教师引导下，以强烈的问题动机为动力、以完成任务为主要标志、以学生自主探索与互动协作为主的教学方式。文章通过设计情境型任务、操作型任务、应用型任务、拓展型任务，以引导学生进行深度学习，从而提升学生的数学核心素养。

［关键词］任务驱动；深度学习；教学策略

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）11-0097-03

深度学习注重培养学生的思维能力与解题能力，倡导学生在真实情境中主动讨论、思考、探索、实践，以达成对已学知识的理解、应用和创新。任务驱动是指学生在教师的引导下，围绕一个共同的任务展开的学习活动，以强烈的问题动机为主要动力、以完成任务为主要标志、以学生自主探索与互动协作为主要方式的学习方式。可见，任务驱动是一种深度学习模式，有助于学生明确学习方向、激发学习兴趣，进行深入探究和深度思考，从而促进深度学习发生。任务驱动教学一般包括任务设计、任务探究、任务展示、任务评价等环节。其中，任务设计是任务驱动教学的首要环节，能够直接影响后续环节的开展。因此，教师在教学中要根据学生的认知基础和已有经验，找准学生的认知起点和最近发展区，设置多元化驱动任务，充分发挥任务的驱动功能，引导学生积极主动地融入活动中，不断提升学生的数学学习能力，促进学习深度发生，发展学生的数学素养。

一、设计情境型任务：在“知”“趣”互融中激发深度学习的动力

“兴趣是最好的老师。”学生的数学学习兴趣是助推学生求知的内在力量。而情境型任务具有丰富有趣的形式，能激发学生的学习兴趣，让学生产生强烈、持久的学习内驱力，促进学生深度思考。因此，教师在教学中要结合教学内容，根据学生的认知特点和已有的知识经验设计情境型任务，并努力提升情境型任务的趣味性、科学性、知识性，增强情境与数学知识的匹配度，努力达到“趣”中有“知”，“知”中含“趣”，“知”“趣”互融，“激”“趣”引思，真正实现深度思考，促进学生数学思维的发展。

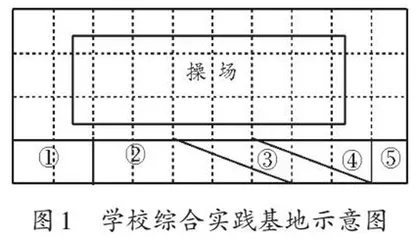
以“多边形的面积公式复习课”为例，教师首先播放学校综合实践活动宣传片，然后说：“大家瞧，这是同学们平时在综合实践基地里辛勤播种、浇水、施肥、除草的影像资料，同学们的付出没有白费，今年的毛豆获得了大丰收。”学生从屏幕上看到自己劳动的样子和丰收的毛豆时，感慨万千。教师此时话锋一转：“一分耕耘，一分收获。大家想不想知道实践基地中的这5块地各收获多少千克毛豆？”学生纷纷表示很想知道，此时教师抛出任务：“我已经将这5块地画在了方格纸上，每小格的边长为10米（如图1）。你们有什么办法求出这5块地各收获多少千克毛豆？”

经过小组讨论后，有学生表示，只要问问农艺工1平方米能收多少千克毛豆，再算出综合实践基地中种毛豆的5块地的面积就可以知道每块地各收获多少千克毛豆。其他学生纷纷表示同意，此时教师出示信息：1平方米大约收0.4千克毛豆。学生得到信息后，纷纷主动计算各图形的面积及各块地能收获毛豆的质量。

上述案例中，教师摒弃传统多边形面积复习课“先回顾面积公式，再运用公式计算”的教学方式，通过引导学生观看综合实践活动影像资料，在学生情绪高涨的时候，抛出问题“有什么办法求出这5块地各收获多少千克毛豆”，这一情境型任务使学生内在的学习需要在不经意间悄然萌发，驱动学生积极思考，主动寻求解题办法，顺势完成多边形的面积计算的复习任务。把多边形的面积计算融入综合实践活动这一情境中，不仅沟通了数学与生活的联系，引发了学生的好奇心，激起了学生的学习兴趣，唤起了学生的学习热情，还使学生在不知不觉中复习了多边形的面积公式，为后续的关联拓展奠定了坚实的基础。

二、设计操作型任务：在“动”“思”结合中推进深度学习的优化

皮亚杰认为，动作是智力发展的起点。通过动手操作，学生能够将外部活动内化为内部认知结构，从而促进智力的发展。操作型任务就是在任务驱动下侧重动手操作，强调多种感官共同参与的一种任务类型。操作型任务使学生能够在实践中发现问题、思考问题，从而引发学生的学习欲望，让学生积极投身到任务中去，主动探究、理解与运用数学知识。在操作任务中，学生在“做中思”“做中说”“思中做”，手、脑、眼、口协同活动，数学直觉、猜想、推理与操作融为一体，“动”中有“思”，以“思”引“动”，“动”“思”结合。这有利于学生经历知识的发生、发展与形成过程，提高学生的动手能力，形成清晰的表象，积累丰富的活动经验，发展学生的几何直观能力。

以“圆柱的表面积”教学为例，教师设计了如下操作型任务。

任务一：每四名同学为一组，利用卡纸制作一个圆柱，在制作过程中把发现的问题和要点及时记录下来。教师在学生分组活动后，组织学生交流，鼓励学生将自己的发现表达出来。学生的分享：“我们小组发现圆柱的表面由上、下两个圆和一个曲面组成，这一曲面展开后是一个长方形。”“我们小组发现圆柱的底面周长和展开后的长方形的长相等。”“我们小组研究圆柱的底面周长和长方形的长之间的关系。”……

任务二：怎样计算你们制作的圆柱的表面积？你觉得需要知道什么条件才能算出圆柱的表面积？小组合作探究，活动中及时与组员交流。

上述案例中，教师把圆柱的知识巧妙地隐藏在操作任务里，虽然所设计的任务并没有提及圆柱侧面展开后的长与圆柱的底面周长的关系，但学生在完成任务的过程中经历了圆柱的制作过程，对圆柱各部分之间的关系有了深刻的体悟，精彩纷呈的感悟表达也就自然生成了。整个活动过程，学生完成了一系列富有挑战性的任务，这极大地激发了学生主动参与数学学习的兴趣，帮助学生自主建构了圆柱的表面积计算方法。在完成操作型任务的过程中，学生不仅真正成为数学学习的主人，成为知识的探索者、研究者、发现者，而且对圆柱表面积有了深刻理解，其思维在实践的土壤中生根发芽，为数学思维能力的发展打下基础。

三、设计应用型任务：在“学”“用”结合中巩固深度学习的效果

应用型任务能驱动学生综合运用数学和其他学科知识解决现实世界中的真实问题。在操作实践、小组合作和交流展示中，学生经历发现和提出问题、分析和解决问题的全过程。这一过程使学生的数学学习由被动变为主动，课堂教学的重心由知识的传授变为能力的提升、素养的培养。学生在体验中自主理解和掌握数学知识，提高解题能力，感悟数学与生活的密切联系，发展学生的数学基本素养。因此，教师在教学中要适时设计应用型任务，使学生在“学”“用”结合、学以致用中深刻理解知识，领悟知识的本质，巩固深度学习的效果。

以“平面图形的面积总复习课”为例，教师设计了应用型任务。教师引出话题：“同学们，愉快的时间总是短暂的，不知不觉我们已在校园里学习、生活了六年，美丽的校园留下我们快乐的回忆，让我们难忘，大家想不想绘制一幅校园平面图留念呢？”学生纷纷表示十分愿意，教师趁热打铁：“要绘制校园平面图，应该怎么做呢？”有的学生说要知道我们的校园里有什么建筑，如食堂、教学楼、花园、操场等；有的学生表示要测量统计建筑物的实际尺寸，这样才能根据实际尺寸按比例缩小画在纸上；有的学生表示可以用步测或米尺进行测量……

通过任务驱动，学生在绘制校园平面图的过程中不仅复习了平面图形面积的计算方法，还在思维的碰撞中找到解决问题的办法，获得了成功的学习体验，实现了知识的内化与创新。整个活动过程中，学生回归真实的生活，切实体会到学有所获、学有所用，感受到数学与生活的密切联系。

四、设计拓展型任务：在“联”“拓”并进中提升深度学习的品质

在数学教学过程中，教师应避免让学生陷入重复学习的困境，而应适时地引导学生进行挑战性的学习活动，让学生“跳一跳才能摘到桃子”。拓展性任务是指教师基于学生的认知特点和学习需求，在学生的最近发展区里设计任务，以挖掘学生的学习潜力，提高学生的数学思维能力，提升学生的数学思维水平。因此，教师应致力于拓宽知识视野、充盈教学内涵，设计适宜的拓展型任务，为学生提供充足的探究时间和空间，以提升学生的数学学科核心素养，让每一名学生获得发展。当然，拓展型任务不是人为加深学习内容的难度、加重学生学习的负担，切不可为了拓展而拓展，不能盲目延伸、任意拔高，而应以夯实基础知识为出发点，聚焦知识本质，适度拓展知识内涵，沟通知识之间的联系，通过引导学生完成拓展型任务，让学生经历知识的探索过程，了解数学发展的历史，揭示数学的规律与奥秘。这样才可以进一步丰富学生的认知结构，拓宽其知识视野，让学生积累丰富的数学活动经验，从而促进学生的数学思维发展。

以“立体图形的体积整理与复习课”为例，教师以长方体、正方体与圆柱体积公式为主线设计了拓展型任务。

任务一：认真观察长方体、正方体与圆柱这三个立体图形，它们有什么相同点？

任务二：为什么都可以用“底面积×高”来计算它们的体积？

通过观察，有学生认为这三个立体图形都可以看成是平面图形（长方形、正方形与圆）向竖直方向“长高”后形成的图形；有学生认为这三个立体图形的体积都和底面积和高有关——底面积一定时，高越大，体积就越大。教师对此予以肯定，随后出示三棱柱、六棱柱、八棱柱等立体图形，引导学生思考：根据长方体、正方体与圆柱的体积公式，怎样计算这些立体图形的体积？为什么这样算？学生通过观察比较，发现这些立体图形上下一样粗，都可以看成是三角形、六边形、八边形向竖直方向“长高”形成的，因此认为它们的体积也可以用“底面积×高”来计算。在验证成功后，教师出示拓展任务：用“底面积×高”这个公式还能计算什么样的立体图形？以此引导学生再次展开观察、猜想、推理、验证，进一步深化学生的认识。

上述案例中，教师充分挖掘立体图形的体积在纵向上的联系，适度关联立体图形的体积公式，以学生学习过的立体图形为纽带设计拓展型任务，使学生跳出认知局限，通过类比、推理、想象、迁移等活动，驱动学生深度探究立体图形（直柱体）的体积公式、平面图形与立体图形之间的联系，深化学生对立体图形（直柱体）的体积公式的理解，最终实现知识、方法与思想的融合，促进学生思维的发展。

综上所述，任务驱动能有效促进学生进行深度学习，而任务设计的科学性直接影响学生的学习效果。在实际教学中，教师要以任务探究为基础，结合实际，设计针对性、趣味性、应用性较强的多元化任务，激发学生的学习积极性，使其在深度思考中主动发现数学现象，积极验证数学原理，不断提升学生的数学思维，促进深度学习真正发生。

［ 参 考 文 献 ］

[1]    王文英.大任务统领：促进学生数据意识发展的思考与实践[J].小学数学教育，2024（22）：4-6.

[2]    李雪峰.巧用实践基地引发数学思考：《多边形的面积复习》教学设计与说明[J].小学教学设计，2021（20）：52-54.

[3]    单蓓蓓.基于任务型教学理念的小学数学作业研究[J].小学教学设计，2024（S1）：100-101.

【本文系广西玉林市教育科学“十三五”规划课题“积极心理健康教育在中小学教育中的应用研究”（2020B456）的阶段性成果。】

（责编    梁桂广）