核心素养导向下的小专题教学反思

一、新课标下初中数学教学

新课标中初中阶段的图形和几何领域，包括“图形的性质”“图形的变化"和“图形与坐标”三个主题。其中“图形的性质"强调通过实验探究、直观发现、推理论证来研究图形，其中“图形的变化”强调从运动变化的观点来研究图形，而本节《手拉手模型》就借助信息技术，通过几何画板动态处理图形的变化，将抽象的数学知识直观化，促进学生对数学概念的理解和数学知识的建构。

二、核心素养导向下的小专题教学

核心素养需要在长期的教学过程中逐渐形成的，核心素养在不同教学阶段的主要表现体现了核心素养的阶段性和各阶段之间的一致性。结合《全等三角形》单元的教学内容，本节研究的是全等三角形中的一种判定SAS，图形发生改变了，教会学生在“变”中找“不变”，手拉手模型中不变的是共顶点、等线段。引导学生在变换的场景中找不变的量，不变的图形等。

“手拉手模型”这一节是一个专题课，本节课是在学习了全等三角形、等腰三角形等知识的基础上，进一步研究由顶角相等的两个等腰三角形共顶点所组成的数学模型手拉手模型的特征。由这个基本模型探究出相关结论，为后续解决以这个模型为基础的问题提供方法。这节课是对等腰三角形、全等三角形等知识的综合应用，同时为后面研究旋转、相似奠定了基础。中学阶段重点研究的两个平面图形的关系是全等和相似，本章将以三角形为例研究全等三角形的问题和研究方法为后面学习相似教学提供思路，而且全等是一种特殊的相似，本节手拉手模型在相似和旋转中也有出现，也是重要的中考考点，中考热点。

以《手拉手模型》专题教学为例，总结模型特征：共顶点、等线段、等夹角得出全等，进一步为后面的结论做铺垫。

中考数学中几何考题的比例很高，尤其是变换图形，添加辅助线作图又是同学们很头疼的事，掌握好图形的简单易懂的模型不仅可以在有限的时间里提高学生的做题速度，而且可以开拓学生做辅助线的视野，让学生感悟图形的抽象，逐渐形成空间观念和初步的几何直观。

数学知识重要，数学方法更重要。小专题教学就很有必要。在教学中注重体现方法的教学，注重体现教学的阶梯性。利用在《手拉手模型》小专题教学中，从两个共顶点的等腰三角形手拉手过渡到两个等边三角形手拉手，再到两个等腰直角三角形的手拉手，最后还有两个正方形手拉手，让学生体会在不同图形情境中，手拉手模型的共性。

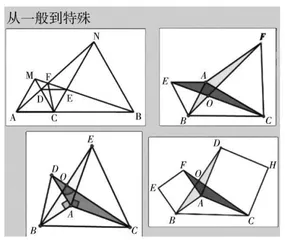
新课程标准要求理解全等三角形的概念，能识别全等三角形中的对应边、对应角等；掌握全等三角形的判定定理；理解等腰三角形、等边三角形、直角三角形的概念，掌握相关性质及判定定理。本节课主要是通过学生观察、讨论、交流，了解什么是“手拉手模型”，培养分析、推理、抽象能力；经探索等边三角形“手拉手模型”常用结论的过程，发展探究意识和合理推理能力；运用“手拉手模型"解决简单问题，感悟具有传递性的数学逻辑，形成几何直观和推理能力。

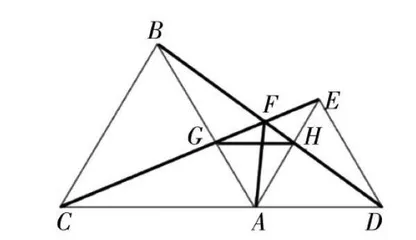
教学中注重学生的归纳总结，推理探究能力。本节专题课分为三大教学环节：手拉手模型的识别、手拉手模型的探究和手拉手模型的应用。在设计手拉手模型识别中，引入模型来源，模型满足的三个条件，并让学生用不同颜色笔描出图中全等的两个三角形并思考全等的依据，由全等还能得到什么，还能在图中找出什么模型，得出什么结论。在模型探究中，合作学习让学生以组为单位，小组成员之间交流，碰撞出思维的火花。合作学习是为了让每一位学生参与学习的全过程，给每一位学生提供展示的空间，使得学生能充分表达自己的观点，经历观察、实验、猜想、推理、交流和反思，不断完善自己的观点，不断产生新的想法。如图2，找出图中几对全等三角形？试一试，看哪一组找得多，并说一说理由。思考由全等你能得到哪些结论？（提示：从边、角、面积等角度考虑）

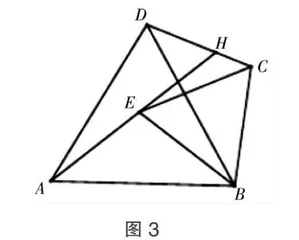
如图3，等边三角形 Δ A B D 和Δ B C E ，连接 A E 与CD，AE与 D C 交于 H 以下哪些结论成立：

①△ABE≌△DBC;②AE=DC;③∠AHD=60°； ④ BH平分 ∠ A H C .

让学生在开放性的问题中深度思考，三角形全等后可以得到哪些结论。最后设计模型的应用，通过添加辅助线构造手拉手模型，最后让学生自己总结一些有用的结论或模型，汇集成题本。

三、教学反思

学生在掌握判定三角形全等的基础上，通过让学生发现如何从“旋转模型”转化成“手拉手模型”，结合动手操作实验更深入地了解“拉手”，进一步总结出“手拉手模型”的一般特征，让学生能够在复杂图形中找到“手拉手模型”，再通过从变化中寻找不变的学习思路，经历猜想、证明的过程得出一般性结论，从而更好地帮助学生解答复杂图形中包含“手拉手模型”的题目。

参考文献：

[1]于志游，莫鄯仟，童莉.单元整体视域下初中勾股定理复习课的教学设计研究[J].数学教学通讯，2024（6）：3-11.

[2]周威.深度教学理念下的微专题教学设计案例探讨[J]数学通讯，2024（2）：43-46.

[3]钱进陆.谈“手拉手模型”的解题思路[J].数理天地，2023（4）：23-24.

[4]陆建明.以“离散型不等式恒成立问题”为例谈高三微专题教学设计的“精准指导"[J]数学通讯，2024（2）：40-41.

责任编辑 徐国坚