基于结构化思维 凸显轴对称本质

图形的运动，又称图形的变换，分为全等变换和相似变换，小学阶段有关图形的全等变换内容为平移、旋转和轴对称。在学习了相关内容后，当提及图形的运动时，学生首先想到的是平移和旋转，而没有将与平移、旋转一样同是全等变换的轴对称视作一种图形，更没有将其看作图形运动的方式。尽管在教师的追问、强调和补充之下，学生最终好像也能接受将轴对称纳入图形的运动范畴中，但对轴对称的理解却简单而狭隘（见表1）

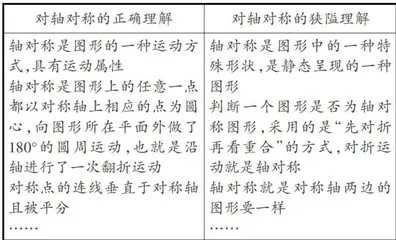
可见，学生虽然按教材编排进行系统的学习，但对轴对称的理解却长期处于狭隘层面。学生为什么会产生概念认识上的模糊现象？教师在教学中应该怎样帮助学生实现对轴对称概念的正确理解呢？

一、学生的理解与困难

学生不容易将轴对称放到与平移、旋转同等的地位，没有将其看作图形运动方式的原因是多方面的。其中，轴对称运动的特殊性、教材编排以及按教材编排逻辑展开教学是重要的原因。

1.概念的名称相对抽象

平移和旋转的概念名称自带“运动基因”，除了能让学生非常直观地感受到“动”的底色，还能从概念名称上快速联想到“动”的方式，而轴对称的概念名称中的直观成分无疑隐晦许多。在学生再次学习轴对称（四年级下册）后，询问学生以下问题（见表2），学生的答题情况也说明了这一点。

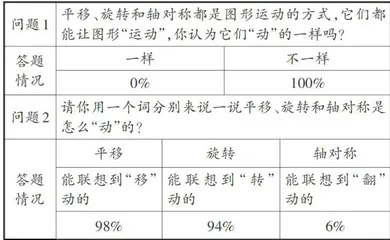
上表说明，面对轴对称这一概念名称时，学生无法马上从中抽取出图形的运动方式，而是需要依靠已建立的图形运动表象与概念名称之间的联结，通过回顾图形具象的运动过程，思索这一图形独特的运动方式该用哪个合适的词汇进行表达。显然，相较于平移与旋转，这一过程与轴对称这个概念名称所具有的抽象性不无关系。如果轴对称的教学没有体现其运动性，那么学生的理解更是难上加难。

2.运动的方式比较特殊

轴对称运动相较于平移、旋转运动有很大的不同，平移、旋转运动都是一个图形在图形所在平面上的二维运动，而轴对称是一个图形上的任意一点都以这点在对称轴上相应的垂足为圆心，向图形所在平面外做了 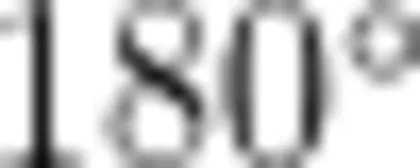的圆周运动，也就是沿轴进行了一次翻折的运动。但学生在学习旋转后，在一定程度上将轴对称这样的翻折运动过程，理解为图形沿对称轴进行了 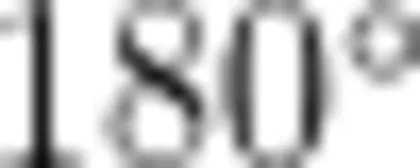的旋转运动。以三角形ABC的轴对称与旋转运动（见表3）为例，其实不管是轴对称还是旋转，就运动过程而言，它们都是以一条直线（对称轴）为轴，向图形所在平面外做了 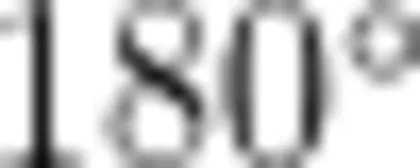的圆周运动。不同在于，轴对称的重点在对称上，意义在于运动前后两个图形要关于一条直线对称；旋转的重点在转动上，强调的是围绕中心进行了怎样的旋转。尽管轴对称与旋转是截然不同的两种图形运动方式，但就翻折的运动过程来看，轴对称这一运动过程中也有旋转的要素。翻折的过程是旋转的，结果是对称的，因此轴对称运动具有复合性，这也给学生的理解造成了一定的影响。

3.相近的概念容易混淆

学生在应用轴对称这一概念名称时，常常会把“轴”这一关键字省略，说成“对称”，而把轴对称图形也简称为“对称”，这说明了学生在概念意义理解上的模糊与混淆。特别是对称轴与轴对称、轴对称与轴对称图形的意义，如果学生不能准确区分，就会造成理解上的偏差与概念上的混淆。因此，学生在理解轴对称概念意义时，必须同时理解与其相关的其他概念。也就是说，学生要理解的不是单一的概念，而是面对一个概念群。这是学生在学习平移、旋转运动时不会遇到的情况，无疑也增加了学生理解上的困难。

二、教材的编排与教学

当前，教材将图形的全等变换内容多分为两个阶段进行编排（见表4），年级上虽略有差异，但整体思路差不多。第一阶段是感受全等变换现象，初步认识图形的运动；第二阶段由表及里，进一步深化认识。这样编排既分散了难点，遵循了学生的认知规律，由感知现象到认识本质，也体现了知识螺旋上升的特点，无疑是科学的一种分段安排。但这样的编排也存在以下一些问题，值得我们思考。

第一阶段：没有彰显轴对称的运动属性。

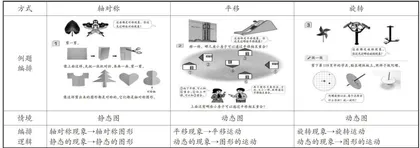
三个版本教材在第一阶段，对轴对称、平移和旋转的编排体系及例题形式总体相似，但轴对称在编排上较平移和旋转有着不同的逻辑，容易让学生产生错觉。以人教版编排为例（见图1），三者都是由生活中的运动现象引入，平移和旋转由相应的平移、旋转现象非常自然地引出了平移、旋转运动。如平移的例题编排，学生能直观感受到一个图形经过运动后可以变换到另一个位置上。按照这样的逻辑，编排轴对称内容时应由轴对称现象引出轴对称运动，这是非常自然的过渡。但实际上，轴对称的编排却由轴对称现象引入转向了对轴对称图形的认识，即从一种运动现象转到一种静态图形的认识，从认识轴对称运动变成了认识轴对称图形。在轴对称内容编排中，始终没有说明轴对称是一种图形运动的方式，素材也没采用和平移与旋转一样的动态图，最后又转向了静态的轴对称图形特征的认识，这样大大弱化了轴对称“动”的底色。虽然教材中有编排"对折"这一动态过程，但学生更倾向于把它作为制作轴对称图形的一种方法。再者，剪纸时左右两边的图形是同时存在的，学生把它看成一个整体图形是非常自然的事情，而不会将它一分为二地理解成是左边的图形沿着折痕翻动到右边的结果。因此，教学后，与学生自然地把平移、旋转看作图形运动方式形成鲜明对比的是：把同属图形运动内容的轴对称不看作图形运动进行了区别对待。教材编排与教学的差别，在一定程度上造成了学生理解的偏差。

第二阶段：不够凸显轴对称的性质特征。

此阶段的轴对称学习，重点在于对轴对称特征的认识，即对称点的连线与对称轴垂直且到被对称轴平分，也就是我们常说的“等距”与“垂直”。不同版本教材在例题编排上略有不同，如人教版和北师大版教材将发现轴对称性质（垂直且等距）和运用轴对称性质（补全图形）分开两个例题编排，而苏教版教材则在补全图形的例题中，让学生在不自觉运用轴对称性质中再识性质。为了帮助学生更好地理解轴对称的性质特征，几个版本教材都选用了比较简洁的图形和格子图。

1.格子图的使用比较单一

在格子图的使用上，不同版本教材都是采用通铺形式，即对称轴左右两边都提供了格子图。格子图的使用降低了作图的难度，学生只要通过数格子数就可轻易发现从对称点到对称轴距离相等的性质。但这样也存在以下问题：

一是对“等距”体验不深。学生在格子图上找对称点只需数格子的数量，并不需要经历实际测量的过程，这极大弱化了学生对对称点到对称轴距离相等的体验。如果对称轴的右边不提供格子图，学生在找对称点的过程中，就要通过测量才能确定对称点的位置。这一测量定点的过程与数格定点相比，能明显加强学生对等距的体验，而这也正是学生多感官体验等距性质的过程

二是对“垂直"体验缺失。通铺格子图上数格定点，在极大弱化学生对等距体验的同时，也导致学生对垂直体验的缺失。因为格子的横、竖线是垂直的，学生在找对称点的过程中只需关注格子数，也就是等距因素就可以了，从头到尾不需要也没机会关注垂直因素。尽管教师引导学生观察补全后的图形，学生似乎也顺理成章地发现了等距与垂直的性质，但这种“看客式”的看图发现，垂直只是一个被告诉的附属品，显然缺失内需式的真实体验。

如在半铺的格子图上补全图形，学生在找对称点的过程中必然要考虑垂直因素。尽管有个别学生受之前学习的影响，会想到在右边补格找点，但大部分学生都能想到将关键点所在的横线反向延长后测距找点。此时，教师只要追问学生“为什么一定要反向延长横线来找对称点？随意画线可以吗？”，就可以引导学生回顾点到直线的距离等知识，这样垂直因素的需求就真正产生了，而学生对垂直性质的理解也更加深刻。

2.关键点的位置可以优化

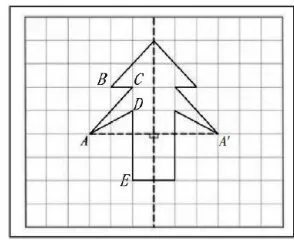
不同版本教材都提供了较为简洁的图形作为素材，图上关键点的个数也比较接近，这样学生操作起来比较合适。如按照点到对称轴的垂线是否与图形的轮廓线重合，点可分为“内、外、平"这三种情况。如小树图（见图2），A点与对称轴的垂线（或部分）会在图形轮廓外部，划分为“外”； C，D 两点则划分为"内”； B，E 两点与对称轴的垂线（或部分）会和图形轮廓重合，划分为“平”。其中，“平"这一种情况比较特殊，因为点与对称轴的垂线刚好和图形轮廓线完全重合。因此，教师将点与对称轴的垂线进行“翻折"演示时，学生不好区分是垂线还是轮廓线在“翻折”。即“平"这一情况的点的个数过多或多点共线，会在一定程度上给学生理解造成干扰。此外，从距离维度考虑，也可以适当减少多点等距的情况。因此，图形素材包含的点的位置情况还可以进一步优化。

三、教学的思考与改进

第一阶段：彰显轴对称的运动属性。

轴对称与平移和旋转一样，归根结底都是全等变换过程中点的运动方式。因此，体现轴对称的运动属性，应该成为不同阶段轴对称内容教学一以贯之的共同理念。那么，在第一阶段教学轴对称时，教师就应该强调轴对称的运动属性，帮助学生形成正确的轴对称的第一印象。为体现轴对称的运动属性，不妨把教材内容作如下修改（见图3）。

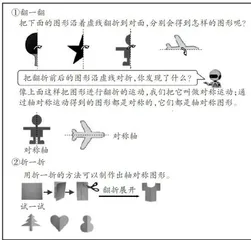
这样编排，解决了上文所提及的本应认识轴对称却悄然转向认识轴对称图形的尴尬境地，逻辑上更加通顺。此外，在对折制作轴对称图形的教学中，除了说明为什么对折可以制作出轴对称图形的道理，教师还要引导学生将翻折展开的过程与轴对称运动建立联系。也就是说，教师要重组现有的教学资源，在教学上作恰当的处理，让轴对称的教学体现其运动属性。