设计数学实验 体验建模过程

2024年人教版初中数学教材注重理论与实践的结合，强调通过数学实验的方式，让学生在动手操作中理解数学概念、掌握数学方法、融合数学实验，构建具有前瞻性的数学模型，来推动数学教学.在教学过程中，教师需精心策划一系列探索性与趣味性兼备的实验，让学生通过亲身实践发掘问题、解决难题，进而深化对数学知识的理解和掌握.笔者以初中数学“探究海拔高度与大气含氧量的关系"教学设计为例，与大家共同探讨如何设计数学实验，帮助学生树立模型观念，体验建模过程.

一、教学内容与素养目标

1.教学内容与学情分析

这节课出自2024年人教版数学教材七年级下册第十二章"数据的收集、整理与描述"中12.2.3节的实验内容.在这一章节中，学生主要学习如何收集数据、整理数据，以及用不同的统计图来描述数据.趋势图作为一种重要的统计图，能够帮助学生更深入地探究两个变量之间的关系，理解数据背后隐藏的规律和趋势

在学习趋势图之前，学生已经在小学阶段对简单的数据收集和整理有了初步的认识，比如会用画“正"字的方法收集数据，能用统计表和简单的条形统计图来呈现数据.升入初中后，学生又学习了全面调查和抽样调查等数据收集的方法，以及用频数分布表、频数分布直方图和折线图等方式来整理和描述数据，这为他们学习趋势图奠定了一定的基础.此时的学生已经具备了初步的观察、分析和归纳能力，但对于如何从更复杂的数据关系中挖掘信息，以及如何用数学语言准确地描述变量之间的关系方面，仍有不足.趋势图相对来说比较抽象，需要学生能够理解散点分布与直线（或曲线）之间的联系，能够通过趋势图预测变量的变化趋势，这对学生的逻辑思维和抽象思维能力提出了更高的要求.在教学过程中，教师需要结合具体的生活实例，引导学生逐步掌握趋势图的绘制方法和应用技巧，帮助他们更好地理解和运用这一知识。

（1）在深入探究一个实例问题时，历经提问、资料搜集、剖析与解决步骤，初识数学在科研领域中的深层含义与价值；（2）在特定情境下，依据数据特性挑选适宜的函数以应对实际问题，并评估所构建的函数模型是否能准确映射数据特征，进而为决策制定提供严谨的科学支撑；（3）在运用函数模型解决现实问题的过程中，个体需主动深思，独立探索，踊跃发问，积累实践操作的基本经验，提升数据与模型的认知，培养应用数学的意识，体会数学在各领域的广泛应用。

3.教学资源

《义务教育数学课程标准》（2022年版）所确立的“总目标”，在指引着教育方向：在义务教育阶段，学生逐步学会运用数学视角审视现实，运用数学思维解决实际问题，并以数学语言描绘现实场景.学生对数学理念间的内在联系及数学与其他学术领域、日常生活的交汇之处有着敏锐的洞察力.在分析现实情境的过程中，学生能够识别并阐述问题，并利用数学及其他学科的知识与策略来剖析与解决问题.数学建模，是数学与现实世界连接的基本方式，本实验按照数学建模的基础步骤设计，即从现实世界的问题中提炼出数学问题，并运用数学语言通过方程、不等式及函数等表达方式，对这些数学问题所蕴含的数量关系及其演变法则进行剖析，计算出具体答案，并对结果所蕴含的深意进行探讨，帮助学生树立模型观念，并深刻体会数学应用的广泛性。

“探究海拔高度与大气含氧量的关系"研究的背景知识如下：相对于海拔较低的平原地区，海拔高度在300米以上的地带通常被称作高原.多数来自平原地区的游客在进入高原地带后，其身体在神经和体液调节机制作用下，会出现一系列适应性调整过程.青藏高原，其海拔3000米以上的低氧环境，是全球高原医学研究的焦点.研究显示，人体在此环境下会出现显著症状和体征，这主要与高原特有的外部环境因素相关，同时，个体体质和地域差异也会影响人们是否出现高原反应.在大气中，氧气的比例约为 20.94% .这一比例对维持生物呼吸至关重要.高海拔区域氧气分压的下降，导致氧气含量绝对减少，引发缺氧现象.若空气中氧气的含量低于 18% ，则会导致人体出现缺氧相关的病征.当氧气浓度下降至 17% 时，肌肉的活动能力将会降低，这表明发生了缺氧症的情况.一般人存活的氧气浓度低限为 10% .经过询问香格里拉市气象局工作人员，我们了解到含氧量一般很难测，很多时候都是先测该地的大气压，不过大气压也和很多因素有关，比如温度、湿度、植被覆盖率、海拔高度等，但主要还是与海拔高度有关。据了解，在忽略了次要因素后，一个地区含氧量 O（%）与大气压P（以kPa为单位）的关系式为 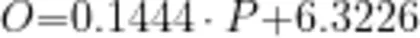，此时，我们就可以将海拔高度与大气含氧量的关系转化为海拔高度与大气压强之间的关系.

二、教学设计的理论依据与创新点

1.研读课标，深度剖析核心素养，精准解析教学内容（如表1）

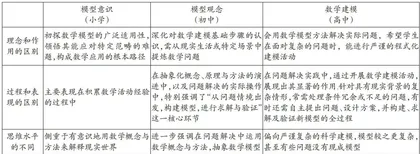
在各个学习阶段，模型意识、模型观念与数学建模作为数学核心素养的体现，其本质一致，却呈现不同风貌。在初级阶段，模型意识与数学建模扮演关键角色，而模型观念则贯穿始终，不仅体现在抽象概念、原理与方法的过程中，亦体现在问题解决的实际操作中.

从原始问题切人，笔者精心构造了多样化的数学建模实践（如表2）

2.创设真实情境，解决现实问题，体验数学建模的基本过程

本实验所提出的教学模式旨在强化学生的数学应用技能、创新意识及解决现实问题的能力，通过创设特定情境并激发学生解决实际问题的热情，促使他们亲历数学建模的各个阶段，进而深人领悟数学在实践中的应用价值.与学生生活紧密关联、富含实际意义的场景与问题，构成了所谓的真实情境。真实情境的构建能在数学教学中点燃学生的学习热情，使他们意识到数学在日常生活和社会发展中的重要作用.同时，真实情境还能为学生提供具体的问题背景和解决方案的参考，有助于他们更好地理解数学概念和方法的实际应用.在为学生提供一个应用数学解决具体现实问题的场景中，教师让他们直接参与到数学建模的基础步骤中去.这个过程不仅涵盖了数学问题的识别、建模、求解和结果解释等关键环节，还提升了学生数学思维能力，且锻炼了创新精神及解决实际问题的能力.通过数学实验，学生能领略数学的奥妙，进而激发其主动钻研数学的热情.创设真实情境、解决现实问题、体验数学建模的基本过程是一种有效的教学策略，能激发学生探求知识的热情与内在驱动力，有助于增强他们的数学理解力与实际运用技能。

3.践行活动育人，积累研究经验，实现核心素养的有效进阶

（1）注重基于核心问题的问题系统的设计

通过问题导向的教学模式推进研究性学习过程，学生需完成从信息搜集、处理、逻辑推演至系统评估和决策制定的一系列认知任务，这有效地推动了学生高层次思维能力的发展。

（2）注重教学语言和研究过程的规范

教师所使用的言辞简洁而精确，学生因此得以自信且自如地以规范化的数学用语进行表达.在查阅文献资料及规范引用等细致环节，学生洞察到了课题研究的学术规范性，在模型检验与优化处理中，学生领略到了课题研究的严谨性，这些课堂教学的点点滴滴，无不彰显着学科育人的价值所在。

（3）注重让学生经历完整的研究过程

在引导学生梳理数学建模常规步骤的过程中，学生通过从具体案例到普遍认识的转化，积累构建数学模型的实践经验，进而为在特定场景下，合理挑选线性、二次或反比例等数学函数，以解决现实问题提供坚实的经验基础。

（4）注重学生核心素养的发展

本实验持续聚焦数学与实际生活的紧密关系，引导学生深刻体会数学在各个领域的广泛应用.运用一次函数模型知识解决实际问题，有助于学生构建模型观念，提升应用能力与实践技巧，并塑造理性思维与严谨的学术态度。

4.融合信息技术，处理信息数据，感悟数形结合的数学思想

采用信息技术整合文献、影像及录音等资源，此举极大地拓宽了教学场域，营造了充满现实气息的问题环境.创设特定情境，不仅强化了数学与生活实际的关联，而且显著地提升了学生探索数学奥秘的激情，极大地促进了他们追求新知识的内在驱动力；借助信息技术手段，教师从形态与数量两个维度强化了学生对于研究主题的深刻理解，通过运用几何画板与Excel，将原本分散的直线汇聚至同一坐标系.将抽象的数学知识直观化、可视化，利用Excel对数据进行处理（计算误差值等），实现对模型的检验与优化，这样的设计促进学生感悟数形结合的思想方法，有效地突破了教学难点。

三、教学设计与意图

数学建模在不同阶段的要求不同，在义务教育的框架内，重点是让学生领会数学模型概念，借助具体案例，感悟数学建模的基本步骤和方法，在初中教育阶段，教师可以组织并实施一系列完整的数学建模项目，使学生得以全面参与，涵盖资料整合、研究报告或小论文的撰写，以及后续的汇报和交流环节，针对特定课题，制定研究方向，构建实验流程，采集相应信息.在本实验课堂上，教师需对数据进行整理和阐述，通过运用数学、物理、地理等领域的知识，引导学生探究数据间的相互关系，确保学生会用数学的思维思考海拔高度和含氧量之间的关系，发现并提出问题。

1.创设情境，提出问题

教师提出问题：“这个国庆假期，我和家人想坐着动车去香格里拉，如果是你，这趟香格里拉之行，你会考虑解决哪些问题？"学生提出了去香格里拉易出现高原反应等问题.教师通过剖析高原反应和缺氧问题，引入海拔高度和含氧量之间的关系.通过信息技术手段对文献、图像、录音等多源资料进行整合，极大地拓宽了教学场景的维度，营造出充满现实气息的问题情境，有效拉近了数学与实际生活的距离，极大地激发了学生探求数学奥秘的兴趣和欲望，并将海拔高度与大气含氧量的关联巧妙地转化为海拔高度与大气压强的内在联系。

2.分析数据，建立模型

通过查阅中国主要城市海拔高度网站和中国气象局网站，教师引导学生得到了中国气象局2024年9月21日14：30的数据，中国部分城市的海拔高度和大气压强如表3所示。

表3中国部分城市的海拔高度和大气压强

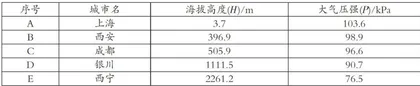
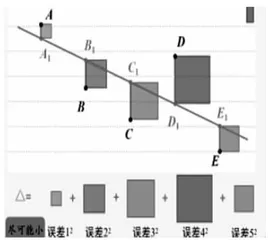
教师提出问题：“能否用更直观的方法来反映数据的变化趋势？”学生开始思考问题.教师再介绍数学家（统计学家）指定能使误差的平方和最小的那条直线的表达（如图1），就是最佳直线的表达式.经过对五个城市的海拔高度和大气压强的数据分析，教师引导学生构建数学模型，从“形”到“数”，经历第二次函数选择，优化所建立的模型，促进信息技术与数学课程的融合.借助几何画板与Excel，学生绘制出相应的趋势图，再将所绘制的多态直线汇聚于同一坐标系，将抽象的数学理论转化为直观可视的形象，通过Excel进行数据处理，如误差值计算等，进而对模型进行检验与优化。