数学教学：追求知识结构与认知规律的有机统一

数学是具有严密逻辑结构的学科，数学专著中的内容大多是按公理化体系编写的。不过，数学知识并不是一下子就严格按这种方式产生和发展的，这种严密的结构通常是在相关知识产生后再进行逻辑化的结果。因此，数学专著（甚至一些数学教材）中的知识体系（包括知识顺序），都不能在教学中照搬。本文以“圆周角"的教学为例，谈谈笔者对此的一些思考。

一、教材中圆周角概念的引入方式

笔者查阅了多个版本的初中数学教材，发现圆周角的概念主要有三种引入方式。

苏科版教材这样引入：

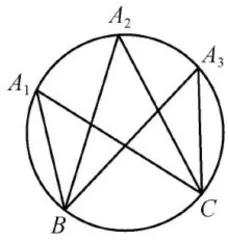
图1中的 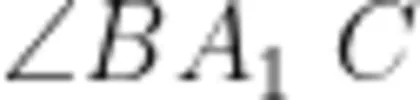、 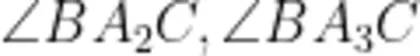有什么共同特征？

这种引入方式是按照数学概念本身形成的思维形式设计的：归纳共性特征，发现本质特点，形成数学概念。但是无法回答“是怎么想到考察这种类型的角的？”这个重要问题，即问题提出的过程不自然。

北师大版教材这样引人：

在射门游戏中（如图2），球员射中球门的难易程度与他所处的位置 B 对球门的张角（∠ABC）有关，当球员在 B， D， E 处射门时，他所处的位置对球门 A C 分别形成三个张角∠ABC、∠ADC、∠AEC，这三个角的大小有什么关系？

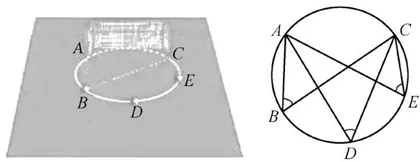
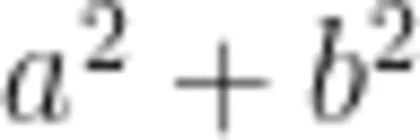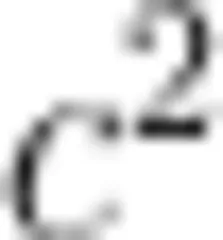这是一个应用性初始问题，从现实背景来看，试图体现引进新概念的必要性，但是同样回答不了上面的问题。这其实是在知道结论的情况下设计的“假情境”，就如一些教师教学“勾股定理"时，让学生对若干个特殊的直角三角形，分别计算 与 ，进而发现 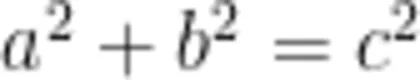一样，学生只是机械、被动的执行者，根本不清楚为什么要这样做。

可能基于对上面两种设计的反思，人教版教材就不设计问题情境，而直接引入了：

在圆中，除圆心角外，还有一类角（如图3中的∠ACB），它的顶点在圆上，并且两边都与圆相交，我们把这样的角叫作圆周角。

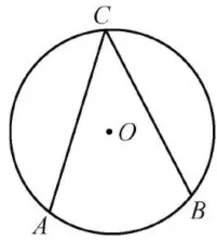
这样引入虽然很干脆，但是显得比较突兀，并且回避了上面的问题一这不是解决问题的办法。

二、历史上圆周角概念的产生过程

历史上第一个提出与圆周角有关的概念的是古希腊数学家泰勒斯（ThaiesofMile-tus，约公元前625一约公元前547）。他是第一个进行数学证明的数学家，他所证明的定理中有“对半圆的圆角是直角”，其中的“圆角"就是圆周角。[1]

欧几里得《几何原本》第三卷中的命题20、命题21即为圆周角定理。命题20：在一个圆中，同弧所对的圆心角等于圆周角的两倍。命题21：在一个圆中，同弧所对的圆周角相等［2]

圆周角最初叫作詹妮特角（Jeanit）。因为它的顶点在圆周上，后将其更名为圆周角。那么，数学家为什么要定义圆周角呢？根本原因在于发现了比泰勒斯定理更一般的结论（圆周角定理）。正由于这样的角有如此美妙的性质（变化中的不变性），才有对其专门命名的必要——其实，泰勒斯已经将其命名为“圆角”，而他之所以对其命名，也是基于发现了很漂亮的性质。至于这个发现的动因，无非是两点。（1）数学家的求真探索精神：发现规律，揭示本质（将泰勒斯定理从半圆推广到一般圆弧的情形）。（2）数学家的审美意识：探求变化中的不变性（量），揭示数学之美。

因此，笔者认为，圆周角概念的产生过程应该是这样的：通过探究，发现这种角具有不变性，说明其重要性，于是有必要专门为其取个名字。事实上，数学中不少概念都是这样形成的，如代数式中的“同类项”，也是因为简化运算过程的需要而自然产生的。

哪怕数学史的过程并不是这样的，从认知的角度看，揭示引进这种角的概念并命名的必要性也是十分重要的。

三、教材编写是“戴着繚铐跳舞”

教材为什么不按历史的过程与认知的规律编写呢？

一般而言，数学内容的陈述有两种方法：一种是按发现和提出问题、分析和解决问题的“问题解决”过程所产生的知识前后关系陈述，另一种是按研究得到知识之后建构得到的相关知识的逻辑关系陈述。3]

教材编写受到很多因素的约束，其中“结构化"是一个基本要求——尽管现在的教材跟30多年前的教材相比，这方面的限制少了很多。因此，教材编写的顺序通常为：概念 表示 分类 关系 运算/判定/性质 应用（因数学分支、内容的不同，会有部分差异）。因此，通常情况下，教材不会将性质置于概念之前。

这样的编写顺序有助于学生对数学知识结构的认识，特别在强调整体教学和结构化教学的现状下更具有现实意义。但是，这种结构并不符合认知规律，也与公理化体系的形成过程不相符。

四、数学教学既要遵循认知规律，又要理解知识结构

历史是最好的启发式。[4]像数学家一样思考，就能切身地感受到“是怎么想到研究这个问题的”，也就自然地认识到新知识的必要性和合理性。另外，学习数学也应该理解数学的知识结构（逻辑关系），充分认识到数学的理性精神这一本质特点。因此，笔者认为，基于数学中公理化知识体系的形成过程设计数学学习过程是一种可行的方法。

数学史上第一本公理化体系的著作是《几何原本》，它是欧几里得在对过往的数学成果进行整理，加以条理化的基础上，用公理结构撰写的。一般地，从历史过程看，数学公理化体系的形成基本上是先有若干个研究成果（零散的，不一定相关），然后进行逻辑梳理，最后形成相应的知识体系。法国的布尔巴基学派就曾用公理化方法将很多数学分支系统化和结构化。历史上，每个具体数学分支、内容的形成与获得往往都不是一蹴而就的，而是经历了相当长的发展、演化过程。在这个过程中，一方面，通过知识的积累，不断为建构数学分支提供素材支撑；另一方面，根据体系的需求，不断补充相应的数学知识。因此，数学分支公理化的过程并不是一个内容（知识点）本身在完善，而是整个数学体系（结构）在完善。两者相互充实、支持，从而达到体系自洽、严密，内容准确、严谨的目标。

下面以“圆周角”的教学为例做简要的说明。

（一）提出问题

谈话：我们知道，圆有很多优美的性质。除了充分的对称性之外，还有很多变化中的不变性，如：圆（周）上任一点处的半径相等（长度）；圆的周长与直径之比为常数 π （长度）；同弧或等弧所对圆心角相等（角度）。

提问：在圆所在的平面上，对确定的圆弧，是否还有其他也具有不变性的角呢？

（二）探究发现

让学生利用平板电脑上的动态几何软件或图形计算器作出 ？ O ，确定 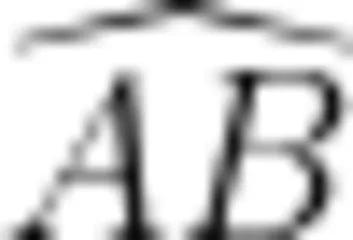（使 ∠ A O B = 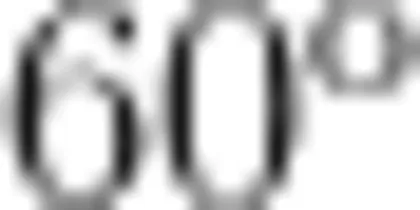），进行探索。

汇报成果：（预设）如图4，当角的顶点 P 在圆的内部时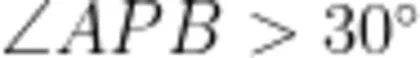， ；当角的顶点 P 在圆的外部时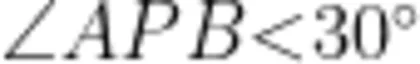， ；当角的顶点 P 在圆上时， 。

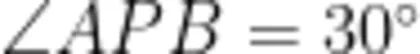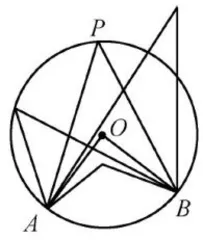
教师再用几何画板呈现探索过程（随着顶点 P 位置的移动，同步呈现对应的 ∠ A P B 的大小），验证学生的发现。

调整 ∠ A O B 的大小，进一步验证上述结论的可靠性。

（三）数学建构

1．通过验证，提出猜想

学生猜想：当角的顶点 P 在圆上时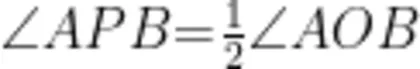， ；当角的顶点 P 在圆内时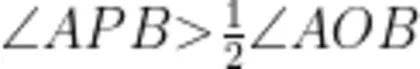， ；当角的顶点 P 在圆外时，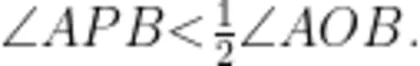

2．归纳概括，形成概念

提问：其中第一个猜想非常重要，说明了圆的一个重要性质，那么，这是一种怎样的角呢？能给它们取一个合适的名字吗？

引导学生归纳这些角的共同特征，概括圆周角的定义（顶点在圆周上），并类比圆心角的定义（顶点在圆心）给这类角取名为“圆周角”。

3．术语表述，逻辑证明

提问：如何用圆周角这个概念表述上面的猜想？提问：如何证明这个猜想？4．考察特例，得出推论提问：特别地，半圆所对圆周角是多大？学生得到泰勒斯定理，并加以证明。（四）数学运用引导学生研究能够运用圆周角定理解决的一些问题（这里省略）。

（五）回顾反思

引导学生回顾本节课的研究过程：基于圆心角定理（不变性） 提问是否还有具有不变性的角 利用信息技术探索 猜想存在一类大小为定值的 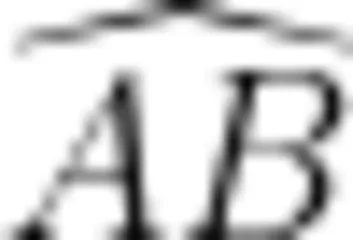的张角 建构圆周角概念 证明圆周角定理（不变性）；形成本节课的知识结构：（概念）圆周角 （性质）圆周角定理 （推论）泰勒斯定理；提炼本节课的思想方法：（提出问题）类比 （探究发现）运动变化 （建构概念）抽象 （证明猜想）分类讨论、转化化归 （发现推论）特殊化。

五、结语

数学教学既要遵循学生的认知规律，又要突出数学本质，建立知识结构。如何做到两者的有机统一呢？笔者认为，应该在探索与建构新知时，遵循学生的认知规律，充分体现发现和提出问题、分析和解决问题的过程，让学生感受到引进新知识（概念）的必要性、合理性，觉得整个过程是自然的；在回顾与反思所学时，在理解研究过程（这是对研究方法的渗透）的基础上，建构知识之间的逻辑关系，形成符合逻辑要求的知识结构。当然，对整个过程中运用的数学思想方法进行显化与提炼，也是提升学生数学素养的必要过程。

参考文献：

[1]梁宗巨.数学家传略辞典[M].济南：山东教育出版社，1989：579-580.

[2]欧几里得.几何原本[M].邹忌，译.重庆：重庆出版社，2005：103-105.

[3]赵慈庚.初等数学研究[M].北京：北京师范大学出版社，1990：122-123.

[4]欧阳绛.数学的艺术[M.北京：农村读物出版社，1997：249.