新时代育人观在数学探究活动中落实“步步为营”的实践探究
作者: 陈晨

中图分类号:G633.6 文献标识码:A 文章编号:1673-8918(2025)14-0082-04
党的二十大报告在育人方面明确指出,“着力培养担当民族复兴大任的时代新人”,青年人要“有理想,敢担当,能吃苦,肯奋斗”,要“敢想敢为又善作善成”。如何才能培养出此种人才?只有通过实践,通过让学生参与到探究实践的过程中,既要检验知识的真理性,又使学生在一次次的深入探究和试错中,消除内心对数学的“畏惧心理”,发展学生的问题解决能力,使学生养成“敢担当、真行动”的实践德行。基于此,教师以数学探究活动为新时代育人观的“实践平台”,以“中国古代数学文化——杨辉三角”为实践探究的对象,让学生在探究中发展能力,感受古人的智慧和魅力,更使学生将文化自信意识扎根心中,打开属于数学的新时代育人画卷。
一、内涵层:新时代育人观的高中数学教学内涵三维度阐释
(一)核心点:学习古代数学文化,厚植立德树人之根高中数学是实现立德树人根本任务的重要学科之一,依据在于:一是,通过数学知识学习,使学生从数学的视角思考问题,形成直观想象和数学抽象;从数学的思维思考世界,形成数学运算和逻辑推理;从数学的语言表达,塑造学生的数据意识和建模能力。此部分为数学学科对学生全面发展的作用,立足于“树人”。二是,通过感受数学知识,体会千年之前古人的智慧,内心深处产生对祖国的自豪之感,热爱祖国。此部分立足于“立德”
(二)落脚点:解密数学文化智慧,孕育数学核心素养
培养学生的数学素养是实现数学立德树人的重要途径。具体言之,教师可借助中国古代数学文化,让学生从数学视角提出问题,从数学思维分析与解决问题,从数学语言交流问题,以增强学生“四能”为手段,塑造学生的数学核心素养。
(三)辐射点:借力数学核心素养,塑造学生数学思维
在以中国古代文化为桥梁的新时代育人观落实上,教师可侧重数学核心素养的“逻辑推理”层面,强化学生的数学思维,让学生在“解构”古人智慧的同时,增强思维的历史性、辩证性、系统性和创新性,使学生“能判断,会选择;能理解,会反思;能包容,会合作”,让学生的数学思维更有“生命力”。
二、逻辑层:新时代育人观与数学探究活动的内在逻辑联系
(一)提出探究活动问题,让学生树立文化自信
提出问题是探究活动开展的初期。在此阶段,教师需要从中国古代文化中的“历史性”入手,并对比此项数学发现在其他地区的产生时间,使学生在对比中,填补对中国古代数学文化的“知识真空”,产生文化自信心,更调动学生的探究兴趣,利于提出相应的探究活动问题。
(二)分析探究活动问题,让学生解密文化智慧
在提出关于古代数学文化问题的同时,学生往往会有一定的“心理预期”,而此种预期是学生数学合理结论的另一种“呈现”。对此,教师可开启探究活动的第二阶段,借助各种条件,包括中国古代文化、个人所学的知识点、教师提供的脚手架等,让学生解决探究活动中所提出的问题,验证学生心中的答案,实现中国古代文化的“解密”。
(三)解决探究活动问题,让学生运用文化智慧
解决探究问题是探究活动的最后阶段,此阶段的主要活动是将古人智慧应用在实际生活的问题解决中。在实际的探究活动开展中,教师既可将生活问题放在探究活动的初期,让学生带着问题走进古代文化的解密中,又可放在探究活动的后期,让学生在“解密”中国古代文化后,运用对古代文化的理解,解决实际问题,真正感受几千年前的古人智慧,让学生对中国古代数学文化产生敬畏之感。
三、脉络层:新时代育人观引领下数学探究活动的构建框架
(一)基于文化场景,提出有意义的问题
在导入阶段,教师可引入数学古代文化,并对比与西方数学文化之间的时代差距,使学生产生文化自信。与此同时,教师可结合古代文化,引入现代数学问题,并直接给出相应的结论,使学生通过简单计算、推断等方式,感受古人的智慧,引出基于古代数学文化方面的问题。
(二)立足所提问题,猜测合理数学结论
在提出问题后,教师可结合实际情况,给予相应的脚手架,使学生借助脚手架,并结合个人所学的知识,进行“直观想象”,提出具有直观性的数学结论,并在此基础上,进一步调动学生的兴趣,推动下一阶段的活动探索。
(三)结合所猜结论,提出验证结论思路
在形成猜测结论后,教师可鼓励学生从中国古代文化的题目条件、个人掌握的数学知识、曾经的数学学习经验和思想等多角度人手,提出验证结论的思路,拟定解决问题的计划,进一步明确实践的方向。
(四)开展具体实践,论证猜测的合理性
在明确方向后,教师可鼓励学生结合拟定的计划,开展数学问题的探究,尤其是秉持“不启不发”的原则,让学生真正在运用个人所学的问题探究中“试错”“改错”,一步步走进真理,体会中国古人的智慧。
(五)用论证解问题,品味中华文化智慧
在学生得出属于个人的结论后,教师可引入生活化问题,让学生结合所得结论,解决此项生活化问题,使学生感受到古人智慧对现实生活的使用价值。与此同时,教师还可引入古人解决问题的方法,使学生以现代的视角,去发现和分析古人解决问题的视角,对几千年前的古人产生敬畏之心,树立独属于中国人的文化自信,品味中华文化智慧的“顽强”生命力。
四、实践层:新时代育人观下数学探究活动的具体实施案例
(一)探究前:引入杨辉三角,对比西方数学,唤醒民族自信
在导入阶段,通过与学生回忆“二项式系数性质”,激发学生对此部分知识的认知,并在此基础上引入如下图1,让学生了解:左侧表在欧洲被认为是法国数学家帕斯卡最先发现的。与此同时,教师引入如下图右侧的杨辉三角,并让学生对比两者的出现时间,使学生感受中国在该方面的数学成就,激发学生的民族自豪感。
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:wjlt20251423.pd原版全文

(二)探究中:立足现代数学,探秘文化智慧,塑造数学素养
1.从图示入手,孕育从形到数思想,引导学生提出两个猜想
(1)巧引入:激回忆,找位置
在初始阶段,教师让学生结合所学的“  与 b 之和的
与 b 之和的 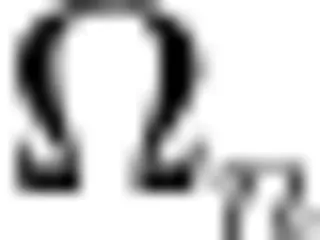 次方的系数规律”,以及图1杨辉三角的数字,大胆进行猜测,完成如下问题:
次方的系数规律”,以及图1杨辉三角的数字,大胆进行猜测,完成如下问题:
① 请写出杨辉三角第9行的数字。
② 请指出 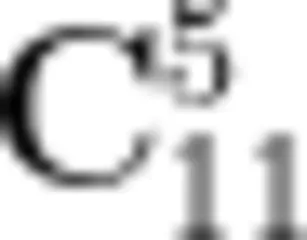 是杨辉三角的第几行,第几个数?
是杨辉三角的第几行,第几个数?
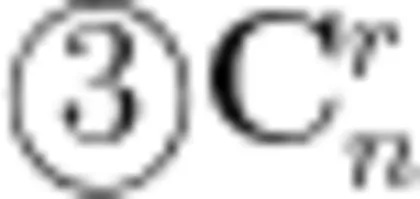 表示的是第几行,第几个数?
表示的是第几行,第几个数?
通过找位置的方式,既可唤醒学生对排列组合知识的认知,并为后续的推理奠定“位置”基础,又能让学生投人数学探究中,初步感受杨辉三角的独有魅力,还可使学生经历由数到形,再由形到数的过程,培养学生的转化思维。
(2)猜想一:观肩头,算合力
在学生明确“位置”的规律后,教师引导学生从“肩头”的角度,观察数与数之间的规律,并展示图2,让学生观察,并大胆猜测。
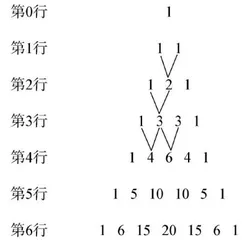
② 能否结合“找位置”的知识,表示第三行“3”与第一行“1"和“2"之间的关系。
③ 请扩大观察范围,运用“找位置”的知识,写出第四行“6”与第三行两个“3”之间的关系。
④ 除最外层的1之外,其余的数等于它肩上的两个数( ),用“找位置”的知识表示为 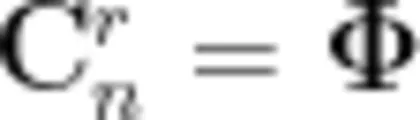
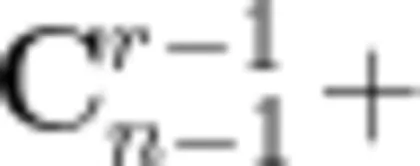 ( )。
( )。
(3)猜想二:观拐角,算数和
在学生完成猜想一后,教师引人猜想二的内容,并展示图3,让学生结合图中所指的线条内容,进行猜想,并尝试扩大现有的杨辉三角范围,进一步验证图中的合理性。与此同时,教师提供如下猜想脚手架:
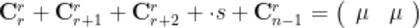
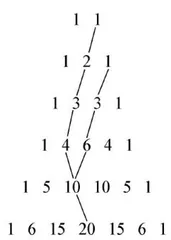
2.从思维入手,激发从数到形思想,启发学生验证两个猜想
(1)从排列组合知识入手,解构猜想一
请证明: 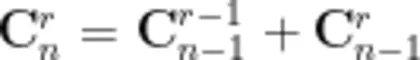 的正确性。
的正确性。
提示:请结合所学的组合数公式。
在展示图2内容后,教师提供如下问题脚手架:
① 请观察第二行的“2”与第一行两个“1”之间的关系。
学生的证明如下: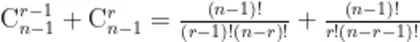
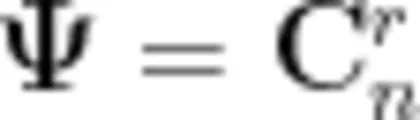 (20
(20
(2)运用猜想一所得结论,验证猜想二
请证明: 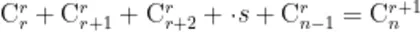 在此部分的证明过程中,教师提示:
在此部分的证明过程中,教师提示:
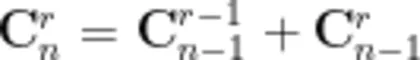
在教师的提示和学生的探究中,进行如下证明:
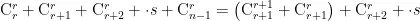
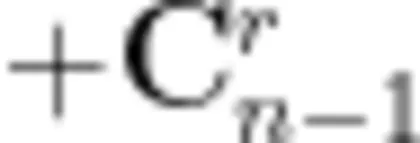
直到化简为 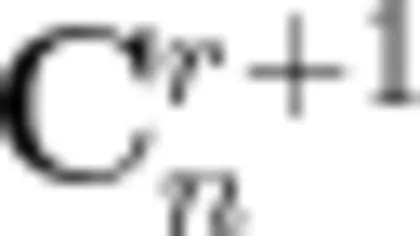 。
。
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:wjlt20251423.pd原版全文