初中数学易错题成因及其解决策略研究

中图分类号：G633.6 文献标识码：A 文章编号：1673-8918（2025）15-0070-04

易错题对学生的学习效果有着直接的影响，还会影响学生的学习态度，所以引导学生及时有效地解决易错题非常重要。学生的学习是一个不断解决错误的过程，而指导学生正视错误，分析错误的原因，才能让学生获得成长。学生犯错是他们思维暴露的过程，教师可以此为契机，对学生开展针对性指导，一来深化学生对学科知识的理解，二来促进学生深度学习的发生。因此，加强对学生易错题解决方法的分析非常重要。

一、初中生数学易错题的成因

学生解题效率不高一直是困扰师生的难题，特别是面对新课标提出的核心素养教学要求，如何在短暂的时间内提升学生的学习效率，成了摆在教师面前的一道重要课题。通过对学生日常作业、课堂小测的检查，文章总结了学生的易错题并深入探寻了学生出错的原因。

第一，前摄干扰问题。经过大量训练，学生已经了解了大概的题型，这就很容易出现“学生一看就懂，一做就错”的现象，并进入同类型问题的陷阱，即便是教师反复讲解、万分叮嘱，依然没有成效。所谓的前摄干扰，指的是学生在接受新知识的过程中会受到以往经验与知识的干扰，导致解题错误。这种现象与学生不良习惯有关，其根源在于学生没有真正掌握知识的本质。

第二，学生对前概念认识不清。学生对前概念的认识是影响学生解题的一个重要因素，特别是在初中阶段，数学概念多且抽象性很强，如果学生在学习中没有真正把握数学概念，便会在解题中出现错误。同时，学生对前后数学概念理解不清，混作一团，也会提高出错率。关于这一点，教师需要在课堂上对学生加以指导，一来解决学生概念不清的问题，二来调动学生的数学学习热情。

第三，忽视题目中的隐藏条件。很多数学练习题存在隐藏条件，如果学生在解题中没有认真分析，便会出现错误。特别是一些综合性的训练题，涉及的知识点多且广，学生只有认真提炼隐藏条件、分析条件间的关系，才能明确解题的思路，开始正确的解题之旅。但一些学生存在读题理解偏差的问题，影响了解题的准确性。

第四，以偏概全。一题多解是初中数学问题的一个普遍现象，比如有理数运算、绝对值方程问题、相似三角形等，需要学生运用严密的思维，综合多学科知识去求解，这对初中生的能力要求很高，不仅需要其具有思维能力，将问题梳理清楚，还需要学生具有分类讨论意识。

二、初中数学易错题的解决措施

数学是初中阶段的一门重要科目，对学生来讲存在一定的困难，以至于学生在学习中总会出现一些易错题，这不仅降低了学生的学习热情，还影响了学生的数学成绩。对此，教师需要认真思考。实际上，学生的错误是被放错了的资源，教师只有合理运用，才能收到良好的效果。

（一）突破生活或相近知识干扰，解决前摄干扰引起的错题

学生在接触新的数学概念之前，已经具备了一定的知识或生活经验，但教师是否提前了解学生的前概念并做出合理的处理，决定了是否会对学生现有知识学习造成干扰。一般情况下，两个知识点既存在相似点但本质又有区别的时候，对学生的干扰作用最大。例如，对“有理数的大小比较”的学习，学生很容易忽视数前面的符号、绝对值等，从而出现错误。仔细分析，是学生没有掌握有理数概念，还是学生没有完全掌握有理数比较的方法。细究之下，可能什么原因都有，但造成学生解题失误的“前摄干扰”因素不容忽视。为了帮助学生消除前摄干扰因素的影响，教师就必须让学生的错误暴露出来，指导学生开展分析，在错误中摸索出一条此类问题的解决方法，从而认识到知识的本质。

1.暴露学生的错误

为了避免学生混淆有理数与小学所学的正整数与负数的概念，教师可以借助例题引导学生思考，让学生在做题中将自己的错误暴露出来，从而正确解决问题。例如：“已知 a > 0 ， b < 0 ，且 ∣ a ∣ < ∣ b 1，尝试比较 a ， - a ， b ， - b 的大小？”有的学生在解题中写道：“因为 a > 0 ， b < 0 ，所以 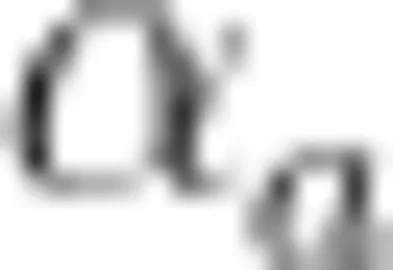在原点的右边， b 在原点的左边，所以 a > b ，又因为 ∣ a ∣ < ∣ b ∣ ，所以 - a < - b 。”对 a 和 - b 的比较，学生一时间会将-b作为负数来比较大小，进而出现了 a > - b 的情况，从而导致答案出错。

2.运用数学方法指导学生比较有理数大小

依然以上述的问题为例，对学生出错的点a > - b ，虽然教师讲了很多遍，让学生在比较的时候认真分析数的正负，但依然有学生会忘记。为此，教师指导学生用数轴的方法比较，首先画出一条数轴，然后根据题目给定的条件 a > 0 ， b < 0 ，可以得知 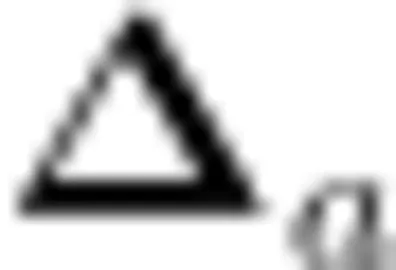距离原点的距离要小于 b 到原点的距离，并在数轴上表示出 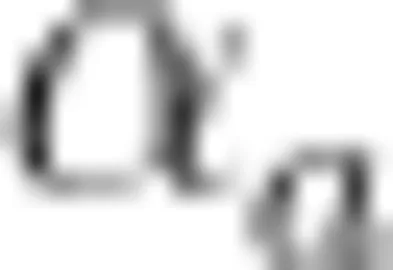与 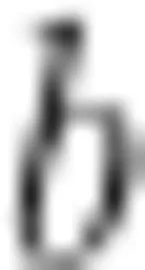，再根据一对相反数在数轴上的位置特点“分别在原点的左右两边并且离开原点的距离相等，在数轴上又可以表示出 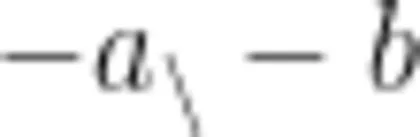，最终得到 b < - a < a < - b 的结果”。对填空题中有理数大小的比较，教师可以指导学生运用特殊值法进行比较，简单方便而且准确率高。

（二）制造矛盾，完善学生的数学概念

在学习数学概念后，一些学生依然没有建立起完整的认知，导致出现概念错用的现象。究其根源在于，学生将现有概念与之前的概念混淆。所谓的前概念就是学生在学习前所具备的概念，可以归纳为正确和错误两个类型。如果学生的前概念正确，那么学生的学习就会出现正迁移；如果学生的前概念错误，则会影响学生对新概念的理解，阻碍学生的学习。因此，教师在组织教学的过程中，要善于制造冲突，引发学生的思考，帮助学生不断完善数学概念。例如，在教学“平行线及其判定”这节内容的时候，借助以下问题：

下面说法正确的是： ① 如若 a / / b / / c ， b / / c ， c / / d ，则 a / / d ② 平行于同一直线的两条直线也相互平行， ③ 垂直于同一直线的两直线互相平行， ④ 过一点有且只有一条直线与这条直线平行。

如图1所示，已知直线 和 b 被直线 所截，下面结论正确的有： ∠ 1 = ∠ 2 ， ∠ 1 = ∠ 3 ， ∠ 2 = ∠ 3 。

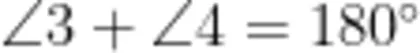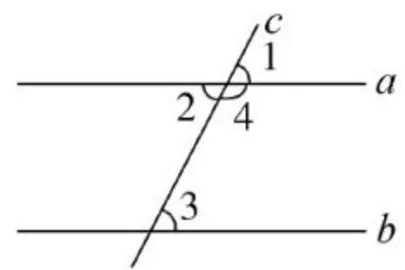
一些学生在解题的过程中出现了错误，对第一道问题，学生忽视了在同一个平面内、过直线外一点这些前提条件；对第二个问题，学生没有明确本道问题的解决关键点“只有两直线平行时，同位角、内错角，同旁内角互补”，这是因为学生的认知还停留在小学阶段，默认平行线就在同一个平面内，默认两条直线就是平行的。所以在初中阶段的教学中，教师要重申这一问题，并通过制造冲突，引发学生的思考，再通过指导学生解释、验证等数学活动，最终实现学生的真正理解。

1.制造矛盾，引发学生的思考

思维冲突不是凭空捏造的，而是在问题的推动下，让学生内心深处产生冲突，处于一种矛盾的状态，最终产生相应的思维活动。故而，关于上面的第一道例题，教师提出了新的问题：“垂直于同一直线的两直线呈现什么状态？你可以举例说明吗？”在问题的驱动下，学生开始认真分析，会思考两条直线在同一平面内、在空间内等各种情况下，这两条直线的状态，从而认识到自己解题中的失误之处。

2.说理辨析，澄清错误

为了帮助学生建立起完善的认知，教师要为学生提供自我交流的平台，让学生在表达中完善自己的认知，解决错误。所以对上述新问题的解答，在学生思考的基础上，教师为学生提供展现成果的舞台，让学生在思维的碰撞下认识到自己的不足之处，并加以完善。

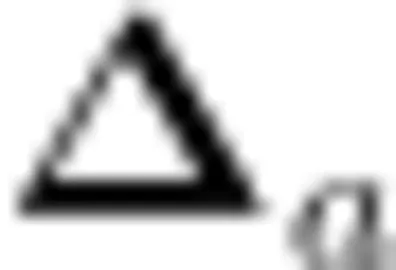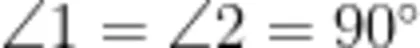学生1：在同一个平面内，如若两条直线垂直于同一条直线，那么这两条直线一定平行，因为直线 b 与 c 垂直于 ，所以 ，所以直线 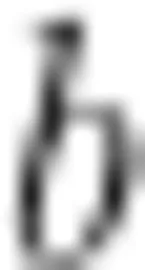平行于直线 ∣ c ∣ 。

这是本课学习的重点内容，大部分学生都能想到。

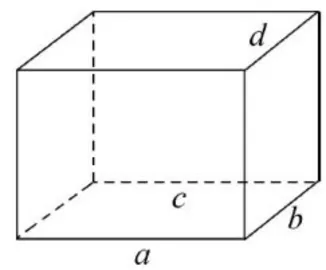
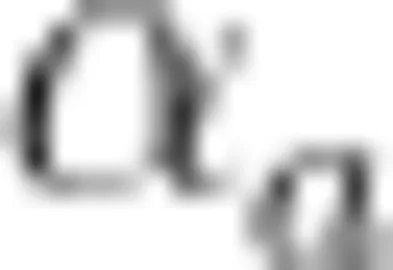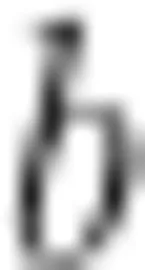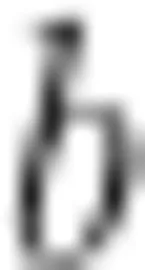学生2：如果两条直线垂直于同一条直线，那么这两条直线的状态如何，还要考虑不在同一平面内的情况，比如在长方体中（图2），直线 和 都与直线 垂直，但是 与 相交，直线 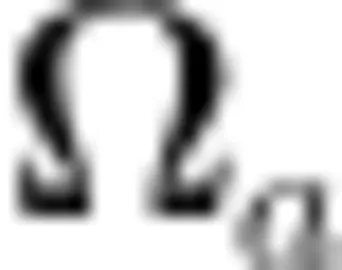与 d 都与直线 c 垂直，但是 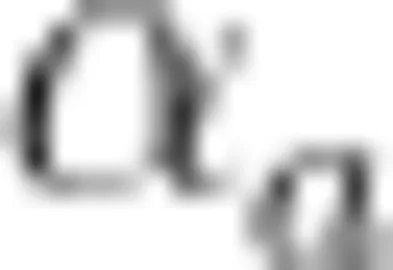与 d 异面，直线 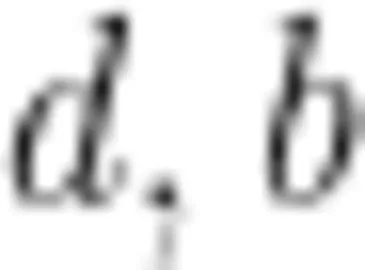与 ∣ c ∣ 垂直， b 与 d 平行。