四边形中的折叠问题

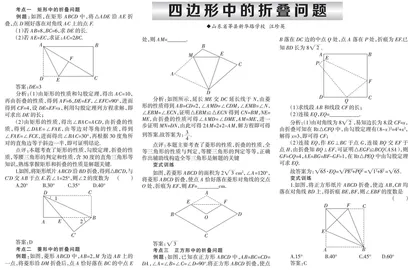
考点一 矩形中的折叠问题

例题：如图，在矩形 中，将 沿 折叠，点D刚好落在对角线 上的点F．

（1）若 ， ，求 的长．

（2）若 ，求证： ．

答案：

分析：（1）由矩形的性质和勾股定理，得出 ，再由折叠的性质，得到 ， ， ，进而得到 ，设 ，利用勾股定理列方程求解，即可求出 的长；

（2）由矩形的性质，得出 ，由折叠的性质，得到 ，由等边对等角的性质，得到 ，进而得出 ，再根据30度角所对的直角边等于斜边一半，即可证明结论．

点评：本题考查了矩形的性质，勾股定理，折叠的性质，等腰三角形的判定和性质，含30度的直角三角形等知识，熟练掌握矩形和折叠的性质是解题关键．

1．如图，将矩形纸片 沿 折叠，得到 ， 与 交于点 ．若 ，则 的度数为（    ）

A．    B．   C． D．

答案   D

考点二 菱形中的折叠问题

例题：如图，菱形 中， ，M为边 上的一点，将菱形沿 折叠后，点A恰好落在 的中点E处，则       ．

分析：如图所示，延长 交 延长线于N，由菱形的性质得到   ，证明 得到 ，由折叠的性质可得 ，进一步证明 ，由此可得 ，解方程即可得到答案．故答案为： ．

点评：本题主要考查了菱形的性质，折叠的性质，全等三角形的性质与判定，等腰三角形的判定等等，正确作出辅助线构造全等三角形是解题的关键

变式训练

如图，若菱形 的面积为 ， ，将菱形 折叠，使点A恰好落在菱形对角线的交点O处，折痕为 ，则       cm．

答案

考点三 正方形中的折叠问题

例题：如图，已知在正方形 中， ， ．将正方形 折叠，使点B落在 边的中点Q处，点A落在P处，折痕为 ．已知 长为 ．

（1）求线段 和线段 的长；（2）连接  ， ．分析：（1）由对角线为 ，易知边长为8．设 ，由折叠可知在 中，由勾股定理有 ，解得 ，即可得 ；

（2）连接 ，作 于点G，连接 交 于点H，由折叠知 ，可证明 ，则 ， ，在 中由勾股定理可求 ．

故答案为： ．

变式训练

1.如图，将正方形纸片 折叠，使边 均落在对角线 上，得折痕 ，则 的度数是（    ）

A． B．     C． D．

【答案】C