从“除法竖式”到“符号语言”的教学思考

在小学数学教材编排中，“除法运算”的内容基本划分成三个知识组块，它们分别是“除数是一位数的整数除法”“除数是两位数的整数除法”“小数除法”。而“除数是一位数的整数除法”又是另两个知识组块的基础，这一内容的知识基础是表内除法（有余数除法）的笔算、一位数除两、三位数的口算。依据教材意图，本课要在原有基础上实现从“表内除法”到“被除数是两位数，除数是一位数，商是两位数（被除数十位没有余数或有余数）”的突破。

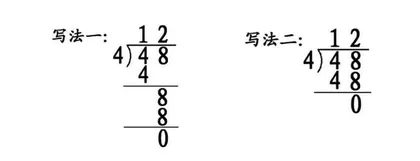
有意义的教学研究应该源于真实的教学困惑，源于真实的课堂。在一次教学自我诊断中，教师对“除数是一位数除法的笔算”第一课时进行了教学解析，并由此构建出一个从尴尬走入沉思，从沉思走向实践，再从实践走向思辨的教研话题。在教学研讨中，一位三年级教师回忆了这样一幕：学生在尝试用竖式进行计算“48÷4”时，出现了以下两种写法：

当教师引导学生对两种竖式进行评价时，学生更多表示出是对写法二的支持，许多学生认为写法一太复杂、没必要。其后的过程，便是教师极其艰难地“说服”学生用第一种写法，并细致分析竖式、反复强调竖式书写的格式和顺序，但事与愿违。

后面的教学讨论中，我们了解到许多教师都在此教学中有着“切肤之痛”。于是，我们在教研组对该问题进行了深层次思辨。针对教师提出的几个有争议的问题，我们教研组经过讨论达成了共识。

问题一：除法竖式到底是什么？

共识：除法竖式是一种数学的符号语言，具有计算与表达的双重功能。

在教学中，一部分教师对于竖式的教学，往往停留在将竖式当作是一种格式、一种规定，简单地告诉给学生，在这样的教学中，竖式只起到了计算的作用，而没有凸显它的表达和显示功能。

问题二：竖式教学需要创设数学情境吗？

共识：需要，情境的最终作用是为学生符号思维的提升提供物质准备。

具体情境是思维的支柱。情境和操作缺失了，学生的符号化过程就无法落实。本课教学的重点是让学生突破从“表内除法商是一位数”到“商是两位数”的竖式表达。“除数是一位数的除法”中所创设的“植树”教学情境，正是让学生经历分两次的过程，以便学生能从这样的操作活动中抽象出数学模型，建立起操作活动、分步口算和除法竖式间的对应联系。

在“笔算除数是一位数的除法”教学中，教师应将除法竖式作为一种近似符号化语言，让学生在现实情境中提炼数学现象、表达数学现象，经历一个较为完整的数学抽象与符号表达的学习过程。当教学研究陷入困境时，教师就要进行更深层次的教学思考与更为大胆的教学假设。

四年级备课组杨老师提出，可否改变例题的呈现顺序，先探究“52÷4”，再学习“48÷4”，先呈现十位有余的情况，这样更有利于学生根据自己的口算与实物操作的经验，对竖式没能表达出“第一次分后有余”提出质疑，会让学生产生正确的竖式表达的需要。

我们的教学思考行进在了很有可能发生重大变化的拐点上，可以向左走，也可以向右走，可能使我们的教学发展向上升，也可能导致我们的教学研究向下坠。两种不同的教学顺序，谁主浮沉？面对拐点，我们的选择便是实践，以学生的学习方式来讨论教学方式，在实践中寻找教学顺序与学生学习体验得以平衡的支点。

我们首先对三年级各班学生就学习数学的能力、算理的理解水平、前期的知识准备进行了前测，选择两个知识水平与学习能力相近的班级进行实验。同时，我们选择了两位教龄相同、教学水平也相当的青年教师参与教学实施。另外，为了保证对学生数学思维信息的全面收集，教研组组织了团队现场观测和课后正确率统计，从两方面对课堂进行全面的观察与测量。

1.算理体验——从“隔岸观火”到“入乎其内”

掌握算法和探究算理是计算教学的两大任务，算法是解决问题的操作程序，算理是算法赖以成立的数学原理。在“先探究48÷4”中，学生对于算理的理解相对比较牵强，在课后访问中我们发现，仍有许多孩子坚持认为式①也能表达“分两次”的过程，而且书写更加简便。而在“先探究52÷4”学生就不得不直面“第一次分后有余”的茫然。式①即

［教学现场］

片断：比较下面两个除法竖式，哪种更能合理地表现我们刚才口算与分小棒的过程？

生1：从书写上看，我觉得第一个竖式更简便，我也能看懂。

生2：我不能从第一个竖式中看到我们刚才分的过程。

生3：我觉得第二个竖式第一层就是第一次分的情况，第二层就是第二次分的情况。

生4：是的，每一层都能让我们看出有多少，分走了多少，还有没有分完。第二个竖式更能表达我们分的过程。

生5：我支持第一个竖式，我可以把第一次分的过程记在心里，这样也很简便。

（课堂上估计大约有三十几位学生认可了第二个竖式的写法，有十余位学生仍然坚持第一个竖式的写法）

从上面的片断中，我们不难看出，“先探究52÷4”，把学生抛置到一个有难度的思维空间，学生会思考用更合理的途径去发现算理、理解算理。虽然，当学生要把更为抽象的竖式计算顺序与形象具体的分小棒过程建立联系，需要延长竖式展现与辨析的时间与过程，但磨刀不误砍柴工，实践证明，学生从竖式计算、口算与操作过程的整体感知出发，更有利于达成竖式计算算理与实物操作过程的正确性。

2.算法掌握——从“食而不化”到“水到渠成”

除法竖式计算时是从高位除起，这和笔算加、减、乘法的计算顺序是不同的。在“先探究48÷4”的口算与分小棒的过程中，可以先算“40÷4”，亦可以先算“8÷4”，不能凸显出“从高位除起”的必要性。学生对于“从高位除起”的算法，只能囫囵吞枣，机械记忆，最终食而不化。而当我们调换了教学顺序后，这一尴尬很快得到化解。

［教学现场］

片断：用分小棒来操作表示“52÷4”。

平均每班种多少棵树苗？

教师请出一个数学学习程度中等的学生。拿到52根小棒时，他首先拿出2根试图分给同学，因为不够分，他马上就停住了，又打算从其中一捆中抽出2根再分。

同学们在下面提示：“先分大捆的，先分大捆的，这样方便！”

他随即顿悟似的拿出4捆，平均分给每个人，再把剩余的一捆打开与2根合起来，平均分给了4个人。

相对于“先探究48÷4”的教学中，因为十位与个位都够除，所以学生对于从“十位除起”只能以机械的方式记忆。而学生在“先探究52÷4”的教学过程中，出现了个位不够分的矛盾后，他们会表现出对“先从高位除起”的认同感。

符号语言的抽象应该是显性操作活动和内隐思维活动的统一。在对学生的思维轨迹进行记录与分析中，我们发现“先探究52÷4”，给学生符号化的过程增加了障碍，更有利于学生实现算理直观到算法抽象的正确迁移，使学生在操作中能有所思、有所感、有所悟、有所得。

我们的课例研究起于思考，收于实践。经历了教材研读、现场观察和数据解构的过程，当所有观点交互碰撞、所有争鸣趋于平衡后，我们沉淀下更为深入、更接近于本质的思考，寻觅到了新的教学智慧：教学“52÷4”时，在学生符号语言的理解上具有思维的优势，然而在学生正确书写竖式的达成率方面，并不存在显著优势。因此，教师需要在理念处理上保持“同构”——要让学生在经历符号语言的抽象过程。在教学实施中，自主选择适合自己的、更适合学生、更适合教学内容的教学方式和行为，灵活地根据学生的学习能力与学习基础选择“异序”。

新的代数课程，从对运算的强调转向更加关注学生能否用数学的眼光把实际的情境数学化、用数学的方法解决实际问题。符号是代数不同于算术的典型特征，当学生从对数的思考、式的思考开始向对符号的思考转变，也就意味着他们开始由算术思维向代数思维转变。因此，运用各种教学途径，帮助学生理解符号表示和符号运算，可以为学生的能力发展提供一个坚实平台。唯有这样，我们的教学研究才能真正体现出它的生命张力和再生力。

作者单位  西安市未央区阿房路一校