分类获得概念 推理验证特征

【摘 要】认识图形的核心是理解它的特征，图形概念的定义与它的本质特征是等价的。以概念形成的途径认识长方形，重要的活动是对四边形进行分类。分类既是获得概念的手段，也是具体的教学目标。一个数学结论的得出不能建立在实证基础之上，用测量与实验的方法验证长方形的特征，可以给我们启发，丰富我们的认知，但不能作为得到数学结论的依据。教学中应重视运用相等关系的传递性进行推理，体现数学在培养人的理性精神方面的独特价值。

【关键词】认识图形 长方形 分类 逻辑推理

认识图形的核心是理解它的特征，教学时分成辨认、认识、探索与证明等明显不同的教学层次。长方形的特征明显，是小学阶段学习的最重要的几何图形。小学生真正认识长方形是从三年级开始的，因为此时的学习关注了图形的特征，并开始积累认识图形的活动经验。边与角是组成平面直线图形的基本元素，认识平面图形一般要关注它的边与角，并且通过测量、实验以及推理等方法研究这些组成元素的关系与特征。

一、分类获得概念

学生理解和掌握概念的过程，实际上是掌握同类事物的共同、关键属性的过程。从同类事物的不同例证中概括发现关键属性，这种概念获得的方式叫作概念形成。用定义的方式直接揭示概念并利用已有认知来理解新概念，这种概念获得的方式叫作概念同化。小学生的认知结构比较简单，可以作为“固着点”的已有知识比较欠缺，往往只能采用概念形成的方式来学习。

认识图形不仅仅是为了让学生知道一种图形叫什么名称或学会区别图形，更重要的是让学生学会对图形分类。

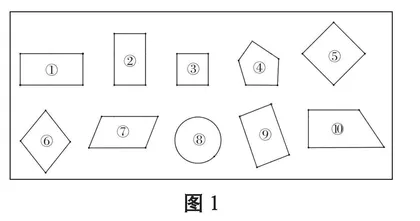
教师出示图1。

图1

师：图1中的图形，哪一个最特殊？为什么？

生：h最特殊，因为其他的图形都有角。

师：（去掉图形h）剩下的图形哪一个最特殊？

生：d最特殊，它有五条边和五个角，其他的都是四条边和四个角。

师：（去掉图形d）剩下的这些图形都是四边形，什么样的图形是四边形？

生：有四条边、四个角的图形。

师：四条边围成的封闭图形是四边形。

师：把这些四条边分成两类，可以怎么分？

生：abcef一类，gij一类。

师：这是根据什么标准来分的？

生：abcef都是对称的。

生：i也是对称的。

师：如果这样调整，把i和abce放在左边，归为一类，f和g放在右边，归为一类，这是按怎样的标准来分的？

生：左边的图形都有直角，右边的图形没有直角。

师：大家同意吗？他是根据是否有直角的标准来分的。

生（齐答）：同意。

师：按这样的标准，图形j应该归到哪一类？它是有直角还是没有直角？

生：有直角。

师：现在，如果把图形j放到右边这一类，左边的图形有什么特点？这时分类的标准又是什么？

生：左边的图形都有四个直角。

师：分类的标准是什么？

生：有四个直角的和没有四个直角的。

师：对于四边形，我们有两个分类的标准—一个是有没有直角，一个是有没有四个直角。你认为哪个分类标准比较好？

学生无答。

师：按照是否有四个直角的标准，我们从四边形中分出一类特殊的图形，这些特殊的图形有一个我们熟悉的名称，是什么？

生：长方形。

师：（指左边的一类图形）这些是长方形，（指右边的一类图形）这些不是长方形，你们能说说什么是长方形吗？什么样的四边形是长方形？

生：有四条边，四个直角。

师：你们说了长方形的特征。如果我们要给长方形下个定义，可以这样说：四个角都是直角的四边形叫作长方形。大家一起读一读。

分类是教学的手段。分类有助于把握问题的本质，了解研究对象的共性与差异，是探索数学对象性质的有效途径。通过分类获得图形概念，归纳概括概念的本质特征，区分非本质特征。概念的定义与它的本质特征是等价的。学生可以再对图形进行分类，并且在了解图形特征的基础上，学习和思考图形的定义。

分类也是教学的目标。分类不仅可以帮助学生获得数学概念，而且能培养数学抽象的核心素养。因为在分类的过程中，既要关注图形的共性，也要关注图形的差异，而共性和差异都是抽象的结果，是抽象的具体体现。在分类的过程中，可以让学生感悟如何合理地制订分类标准并学会遵循标准合理地分类。不同的分类标准，得到的结果是不一样的。一个好的分类标准，要遵循“相互独立，完全穷尽”的原则。所谓完全穷尽，就是所有的对象都可以分到相应的类别中去；所谓相互独立，就是指没有一个对象既可以分在这一类，又可以分在那一类。

概念形成过程实质上是抽象出某一类对象或事物的共同本质特征的过程。概念形成教学的策略是“先分再类”，基本路径：先呈现各种与概念相关的正例与反例，再选择合理的标准把正例分离出来，然后从分类得到的正例中归纳出共同的关键属性，最后区分属性的从属关系并用语言概括成为概念的定义。

二、推理验证特征

图形的认识主要包括两个方面：一是对图形自身特征的认识，二是对图形各元素之间、图形与图形之间关系的认识。其中，对图形各元素之间、图形与图形之间关系的认识，主要包括大小、位置、形状之间关系的认识。根据这些认识图形的要求，可以设计出丰富的图形操作活动，这些操作活动不仅有利于学生理解图形的特征，而且可以帮助学生积累数学活动的经验。

长方形的特征不仅丰富而且直观，如对边相等，四个角都是直角，对边平行，对角线互相平分，等等。学生通过观察，很容易发现长方形的对边相等以及四个角都是直角。可是在数学上，观察得到的经验和结论，不能成为得到数学结论的依据。只有得到了证明，才能形成普遍性的定理。

师：我们已经知道长方形有四条边，四个角都是直角。它的边有什么特征？怎么验证四个角都是直角？请你们用长方形的纸，用自己喜欢的方法发现边的特征，验证角的特征。

（学生独立活动）

师：说一说，你们发现或验证了什么？请把你们发现与验证的方法分享给大家。

生：我测出了长方形上面和下面都是16厘米，左边和右边都是10厘米。

师：上面的边与下面的边叫作一组对边，左面的边与右面的边是另一组对边。他通过测量得到了什么结论？

生：对边相等。

师：还有用其他方法也得到了这个结论的吗？

生：我是将长方形上下对折，两条边可以重合，是一样长的；左右对折，两条边也能重合，一样长。

师：用对折的方法也能发现对边相等的特征。

师：除了关注边的特征，还应关注它的角。哪些同学验证了角的特征？

生：我用三角尺的直角去量，尺子的这个地方是直角，把边与边对齐，知道都是直角。

师：四个角都是用这样的方法来量的，对吗？

生：是的。

师：有没有量的次数少一些的方法？

生：如果对折的话，角是一样的。

师：他说的是什么意思？谁听懂了？

生：我也是这样的，就是把长方形先上下对折，再左右对折，这样四个角就重叠在一起了，只要量一个角就知道它们都是直角了。

师：用实验与测量相结合的办法，可以更方便地验证四个角都是直角。

测量与实验都是操作活动。为了理解与巩固图形的特征，学生应该在多样的活动中比较和讨论图形特征，经历丰富的操作活动。但是，数学结论不能通过经验总结出来，通过测量与实验等操作活动来验证一个结论是不被允许的，数学结论只能从逻辑出发，通过推理得到。

师：刚才我们通过测量与实验，知道了长方形的特征是对边相等、四个角都是直角。正方形也有这样的特征吗？我们怎么验证？

（学生独立思考、操作）

师：用测量的方法来验证正方形对边相等、四个角都是直角，显然是很方便的。除此之外，有没有其他方法？如果不用测量工具，能不能验证结论？

生：我把正方形折成三角形（沿对角线对折），再对折一次，四条边就重合在一起了。

师：哦，是这样吗？（指着黑板上的正方形纸）大家想象一下，能做到吗？

（学生想）

师：来，你来说，我请另一个同学配合你操作。

生：先把正方形斜着对折，得到一个三角形，再把三角形对折，得到一个更小的三角形。

师：结论是什么？

生：四条边重合在一起，正方形的四条边都是相等的。

师：好神奇呀！

师：有同学采用了类似于验证长方形的方法，如图2。上下对折可以得到什么结论？

图2

生：①=③。

师：左右对折得到的结论是什么？

生：②=④。

师：现在我们知道正方形的对边相等，可是怎么才能得到四条边都相等的结论呢？

（学生独立思考）

师：如果斜着对折一次，可以得出什么结论？

生：①=②，④=③。

生：哦，我知道了。

师：你发现什么了？可以跟大家分享一下吗？

生：①=③，②=④，①=②，这样就知道了①=②=③=④，四条边都是相等的。

师：他说的意思你们能听懂吗？

生（少部分）：能。

师：指着图形把这个推理的过程说一说。

教师根据学生的表达，板书：

师：因为①既等于③，也等于②，所以①=②=③。同时，②也等于④，所以①=②=③=④。请同学们看着图示，把这个推理过程先自己说一说，再同桌一人说、一人听。

推断、检验和证明对正方形特征的猜想，可以有多种不同的方法。推理的方法有其独特的教学价值。“实验为实，推理为真”，把实验和推理相结合，着重点在于利用相等关系的传递性进行推理。特别地，相等关系的传递性是很重要的，即如果a=b，b=c，那么a=c，它是代数推理的基本事实。

数学推理反映的是一种基本的数学思想，也是一种主要的数学方法。它与数学证明紧密关联，数学推理与证明共同构成了数学最重要的基础。

在直角三角形中，两条直角边的平方和等于斜边的平方。中国汉朝《周髀算经》记载，早在公元前1000年，周公和商高就谈到“勾三股四弦五”，而毕达哥拉斯则是在公元前500年左右发现了这个定理。在中国，它被称为勾股定理，在国际上通行的叫法却是毕达哥拉斯定理。事实上，毕达哥拉斯也是将数学上升到系统性学科的第一人，他确立了数学的起点，即必须遵循严格的逻辑证明才能得到结论的研究方法，这让数学从早期那些需要靠测量和观测的学科中脱离出来，使数学成为具有方法论性质的特殊学科。

【参考文献】

[1]曹才翰，章建跃.数学教育心理学[M].北京：北京师范大学出版社，2006.

[2]史宁中.基本概念与运算法则：小学数学教学中的核心问题[M].北京：高等教育出版社，2013.