跨学科主题式学习的单元整体教学设计

【摘 要】文章以人教版数学五年级上册第六单元“多边形的面积”为例，聚焦数学学科，创设真实情境，以主题任务为统领，经历实现素养导向的目标设计、整合课堂设计、学用相长的学习过程，实现新课标指导下新课堂的思考。

【关键词】小学数学 单元整体教学 主题式学习

《义务教育课程方案（2022年版）》明确指出，原则上，各门课程用不少于10%的课时设计跨学科主题学习。在新课标理念的指导下，初步对“跨学科主题式学习的单元整体教学设计”这一主题进行研究。基于前期研究，初步意识到各科跨学科主题学习应该是基于本学科内容展开的。教师应聚焦数学学科，立足学科内容，创设真实的，有意思、有意义的学习主题。将数学知识的学习融入主题式学习中，将发展数学核心素养浸润于结构化知识建构中，使学生的学习由数学知识的系统化走向数学思维的逻辑性，应是跨学科主题式学习的单元整体教学设计的实施路径与目标。

基于以上思考，以人教版数学五年级上册第六单元“多边形的面积”为例进行深入思考。单元整体教学设计思路分为五步：（1）依据新课标“纵向·横向”整体分析单元内容；（2）课前访谈，全面把握学情；

（3）立足核心概念，结合生活实际确立单元主题；（4）设计素养导向单元教学目标；（5）基于真实情境设计单元整体教学结构。

一、依据新课标“纵向·横向”整体分析单元内容

（一）纵向分析与本单元教学相关的内容

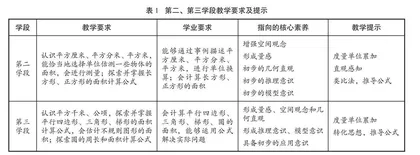
对比分析两个学段，不难看出面积的学习具有一致性，即“度量单位的累加”，在此基础上建立不同图形面积的计算模型。学生数学核心素养的发展呈螺旋式上升趋势。如第二学段形成初步的推理意识、初步的模型意识等，第三学段则是形成推理意识、模型意识。同时，增加了初步的应用意识（表1）。“多边形的面积”这一单元起到承上启下的作用，为进一步学习圆的面积和立体图形的表面积打下基础。

（二）横向分析本单元教学内容

本单元内容分为五个部分。其中前三个部分内容属于面积公式推导计算课，后两部分内容属于解决问题应用课。在这样一个结构中，不仅能帮助学生深入理解面积概念的本质，还能让学生体悟到通过探索图形之间存在的内在联系，将未知转化为已知的“转化思想”。（图1）

图1

二、课前访谈，全面把脉学情

学习前，我们对学生进行了访谈，访谈内容：长方形的面积怎样计算？怎样推出长方形的面积计算方法？

通过分析访谈结果可知，在本单元学习之初还需要开展回归度量本质的过渡性学习活动。同时，课上加强面积公式推导过程的探索，让学生经历知识的形成过程。

三、立足核心概念，结合生活实际确立单元主题

本单元的核心概念是面积学习的本质，即“度量单位的累加”。本单元的核心思想是“转化”思想。从数学角度分析本单元就是一个小的知识团，具有很强的知识体系。学习单元之初，运用长方形的学习经验，探究平行四边形的面积，这个过程出现了不满格的现象。学生通过拼组、割补等方式解决不满格的问题，在深入理解面积概念本质的同时，自然产生转化思想。随后通过探索图形之间的内在联系，将三角形或梯形转化成平行四边形或长方形，推导出面积计算公式。这个过程体现了解决问题的一致性。

如何将多个图形面积计算的学习纳入一个完整的真实情境中，将隐性的核心概念转化为显性的大任务，使学生在解决真实问题中探究数学知识，基于前期“一片叶子”的研究，确定了“校园绿化方案预算”这一单元主题。

四、设计素养导向单元教学目标

基于以上分析，设计素养导向的单元教学目标，并对应单元目标细化三节课的课时目标（表2）。

其中，对应单元目标2和单元目标3，三节课中都有充分体现。由此可以看出，本单元在核心概念的引领下，充分体现了研究方法和数学思想的一致性。

对应单元目标4，针对大任务，三节课分别有自己的小任务目标细化落实。通过三节课小任务目标的达成，最终达成单元目标4。从而看出，本单元在真实情境统领下，学用相长的整体设计思路。

五、基于真实情境设计单元整体教学结构

对于单元整体教学结构的设计，采用以主题式数学活动为主线的单元课时协同设计策略，从两个维度进行：一是源于学生视角的大任务，它是学生进行主题式学习的载体；二是源于数学知识内在联系的核心概念及思想，它是助推学生深入思考的原动力。两条主线相互融合，形成将数学知识学习纳入主题实践的设计思路；同时，有助于学生经历知识形成过程，像专家一样思考问题、分析问题。以此设计思路为指导，将整个单元教学过程归纳为三种课型：单元统领课、单元模型建构课、单元实践应用课（图2）。

1.单元统领课

单元统领课明确本单元实践主题，并通过师生共同探讨，将实践主题分解成若干小任务。与此同时，构建整个单元数学知识体系。

在单元统领课之前，根据确立主题的特点，融合美术课。美术教师针对学生绘制的“校园绿化方案”，从美观、实用等角度进行评价。

2.单元模型建构课

单元模型建构课延续单元统领课的学习方法进行深入研究，学生思维源于第一节课高于第一节课，构建知识模型，体现研究方法的一致性，实现思维的进阶。

3.单元实践应用课

单元实践应用课是对单元统领课的回应，并利用前两节课的经验，进行拓展、应用、提升。

三节课在一个真实情境的统领下，学生在逐一完成每个小任务的同时学习数学知识。将发展数学核心素养浸润于结构化知识建构中，学生的学习由数学知识的系统化走向数学思维的结构化。

跨学科主题式学习的单元整体教学设计，以主题任务为统领，实现素养导向的目标设计、整构成链的课堂设计、学用相长的学习过程，打造新课标指导下的新课堂，探索学科育人的新路径，拓展生活数学的新实践。

【参考文献】

中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022.