依托结构化活动发展整体性思维

作为拔尖创新人才的核心能力之一，学生思维能力的培养至关重要，而思维能力培养离不开结构化的课程设计。笔者以人教版数学四年级《平行四边形的认识》教学为例，谈谈如何通过设计结构化活动帮助学生形成整体性思维。教学这部分内容时，笔者依据结构化理论制定了如下教学目标。①通过观察、猜想、操作、推理、验证等活动探索并掌握平行四边形的特征，发展数学抽象思维、几何直观和空间观念等核心素养。②感悟平行四边形与长方形、正方形之间的联系和区别，体会概念的内涵与外延，形成对四边形知识体系的整体认知，培养整体性思维。③经历结构化的研究过程，积累研究平面图形的活动经验，掌握认识平面图形的一般研究方法。为达成教学目标，笔者预设了“观察—猜想—验证—比较—关联”等结构化活动。

一、观察——辨别四边形异同

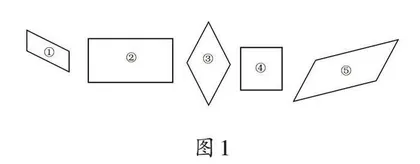
笔者出示图1，让学生观察5个图形有什么相同与不同之处，并将相同的图形分成一类。

学生通过观察，结合以前学过的知识很快把②和④各分成一类，接着把①③⑤分成一类。笔者充分尊重学生的认知基础，有意识地将长方形和正方形的特征按照边、角两个方面进行整理和对比，让他们明确正方形是特殊的长方形。这样做的目的，是引导学生聚焦长方形和正方形的主要特征及两者之间的关系，明晰研究长方形和正方形等平面图形可以从边、角入手，为学生进一步研究平行四边形的特征做铺垫。

二、猜想——猜想平行四边形特征

本环节重点是启发学生通过观察，借助已有知识经验，从边、角两方面猜想平行四边形的特征。

教学中，笔者隐去图1中的长方形和正方形，只保留平行四边形，并提问：“观察3个图形，猜一猜，平行四边形的边和角可能具有怎样的特征？”学生通过观察，提出平行四边形可能“对边平行”“对边相等”“对角相等”等猜想。笔者这样做既掌握了学生对平行四边形的已有认知，又为接下来的教学确立了方向。

三、验证——动手操作验证猜想

验证环节，笔者启发学生借助量一量、折一折、剪一剪等方法自主探究，验证上述猜想。

笔者首先要求学生小组合作学习，完成以下任务。任选上图中的一个平行四边形，逐一验证上述猜想：①量一量——量出四条边的长度和四个角的大小；②移一移——用尺子平移，验证两组对边是否分别平行；③说一说——平行四边形的边和角有什么特征。学生借助量一量、尺子平移等方法动手操作后发现：用尺子量4条边的长度，可以验证平行四边形的两组对边分别相等；用量角器量4个角的度数，可以验证对角的度数分别相等；用尺子平移发现，平行四边形的两组对边分别平行。

为了帮助学生多角度论证猜想，笔者设计了“把一个平行四边形剪成两个一样的三角形”的操作活动。活动要求：①剪一剪——把一个平行四边形剪成两个一样的三角形；②叠一叠——把两个三角形叠在一起，看是否完全重合；③说一说——平行四边形的边和角有什么特征。学生动手操作后，出现了以下两种不同的剪法（如图2、图3）。

剪法一：

剪法二：

这两种剪法互为补充，笔者利用全等三角形“对应边相等，对应角相等”的性质，论证了平行四边形“对边相等、对角相等”的特征。尽管全等三角形的性质知识学生尚未接触，但是因为这样的论证过程是借助剪一剪、叠一叠等直观手段呈现的，所以对于学生而言理解并不困难。更重要的是，学生在经历大胆猜想、小心论证的过程中潜移默化地形成了推理意识，提升了思维品质。

四、比较——探索概念本质

通过猜想和验证，学生发现了平行四边形有三个重要特征：①两组对边分别平行，②两组对边分别相等，③两组对角分别相等。然而阅读教材后，学生发现教材上对平行四边形概念的描述是“两组对边分别平行的四边形”。究竟是需要同时具备三个特征才叫平行四边形，还是只具备这一个特征就叫平行四边形呢？为了解决这个问题，笔者提出一个问题：如果只选一个特征描述平行四边形，你会选哪一个？相应的，笔者设计了“补全平行四边形”的活动。

画一画：分别在图4、图5中补全平行四边形其余的两条边。

说一说：你是利用什么特征补全平行四边形的？

学生在补全平行四边形的过程中体会到，图4必须利用“两组对边分别平行”的特征才能补全，图5可以利用“两组对边分别平行”的特征，也可以利用“一组对边平行且相等”的特征。笔者追问：“在补全平行四边形的过程中，哪个特征必须用到？”学生在比较中发现，“平行”是平行四边形最典型、最本质的特征，“平行四边形”的名字即由此而来，从而顺理成章地揭示出“平行四边形”的概念。

五、关联——促进思维发展

最后一个环节，笔者设计了两个问题引导学生讨论长方形、正方形、平行四边形、四边形之间的关联：①长方形是平行四边形吗？②长方形、正方形、平行四边形、四边形之间有什么关系？

为了解决问题①，笔者出示用吸管制作的平行四边形教具（如图6），并拉动这个长方形，让学生观察、思考：什么变了？什么没有变？学生发现不管怎么拉动，“两组对边分别平行”这个特征始终不变，并由此体会到长方形是特殊的平行四边形，特殊之处在于四个角都是直角。笔者小结并梳理平行四边形、长方形、正方形三者之间的关系（如图7），让学生进一步明晰正方形是特殊的长方形，长方形是特殊的平行四边形。

对于问题②，笔者出示韦恩图，引导学生把四边形、平行四边形、长方形、正方形填入图中，得出图8所示的关系图。

这样做的目的是厘清平行四边形概念的外延与内涵，明晰四者之间的区别与联系，并将平行四边形概念纳入四边形的大概念，帮助学生完善对四边形的整体认知，形成整体性思维。

（作者单位：武汉市育才第二小学）