基于学习起点的深度探究学习

《义务教育数学课程标准（2022年版）》将第一、二学段“位置”相关内容从“图形与几何”领域调整到“综合与实践”领域。这意味着这部分内容的教学在落实显性的知识技能目标的基础上，要更加关注学生参与活动过程中可能经历的思维过程和情感体验，以及可能采用的学习方法和问题解决策略等，以更好培养学生的空间观念和数形结合思想。下面，笔者以《用数对确定位置》的教学为例做具体分析。

一、设计前测，找准学习起点

奥苏贝尔指出，影响学习的最重要因素是学习者已经知道了什么。为明晰学生对用数对确定位置的了解有多深，其教学难点是什么，笔者利用两道题做了学情前测。

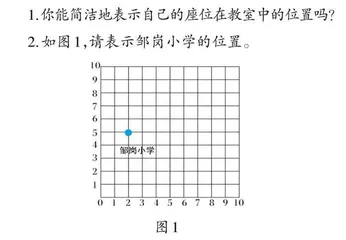
1.你能简洁地表示自己的座位在教室中的位置吗？

2.如图1，请表示邹岗小学的位置。

第1题的前测结果显示：43.58%的学生画图表示，51.28%的学生用文字表述，5.13%的学生用“X7，Y4”等形式的符号表示。笔者发现：学生都能用列和行两个信息确定自己的位置，但先表示行再表示列的人数较多，这与数对的表示次序有冲突。

第2题为学生提供了方格图。在方格图的提示下，用符号表达的学生人数达到了93.5%，占比明显提升。其中，用“5 2”或“2 5”形式表示的人数最多。

通过前测，笔者发现，学生容易理解和掌握用数对确定位置的技能，本节课的教学着力点应该是坐标思想的渗透和数形结合思想的体悟。

二、研读课标和教材，明确目标和任务

为避免教学陷入“辛辛苦苦带学生走冤枉路”的境地，教师要明确课程标准的相关要求和教材的编写意图，结合前测结果制定以核心素养为导向的目标和任务。

笔者在研习新课程标准中11个数学核心素养具体内涵的基础上，秉承通过知识教学达成素养目标的理念，从基础知识、基本技能、基本思想、基本活动经验四个维度制定了具体的表现性目标：①经历用数对确定位置的过程，体验统一规定的必要性和合理性；②体验数对的简洁性与概括性，感悟规定明确是表达简洁的前提；③感知数对对应平面一个点，建立一一对应思想和函数思想；④在探究过程中培养学生的空间想象能力和推理能力。

针对表现性目标①②，笔者设计任务一。

运动会上，邹岗小学学生集体表演，内容是通过人员位置和肢体动作变换展示出学校名称。如图2，怎样描述圈出的这名演员的位置呢？独立思考，描述出该演员的位置；完成后，小组交流，把你这样描述的理由说清楚。

针对表现性目标③④，笔者设计了任务二。

在图2中标出以下位置。第1组：（40，7），（40，8），（40，9），（40，10），（40，11）。第2组：（10，20），（11，20），（12，20），（13，20），（14，20）。第3组：（30，5），（31，6），（32，7），（33，8）。观察每组各点的位置，把你的发现写下来，完成后小组交流。

任务设计没有用例题中的座位图，是因为学生之前学习的前后、上下、左右等方位具有相对性，不方便交流，而采用点子图更容易与坐标图联系起来，方便学生探究。

三、基于核心任务，展开活动探究

任务一：创设情境，掌握表示方法。课始，笔者播放介绍2008年奥运会开幕式上倒计时活动设计构想的视频。这个活动由2008名演员共同完成，导演需要提前把每个秒数对应要点亮的灯箱位置确定好，然后相应的演员在相应的时刻一齐点亮灯箱，达到整齐划一的亮灯场面。邹岗小学想仿照这样的方式，让学生把校名展示出来。我们怎样把演员的位置描述清楚呢？随后，笔者呈现任务一，引导学生结合真实情境感受确定平面上物体的位置需要行和列两个要素，探究用数对确定位置时“先列再行”规定的合理性，掌握用数对表示位置的方法，体会这个表示规则与直角坐标系的一致性。

学生自主探究后，笔者呈现如下学生作品。作品一：从上往下数第11行，从左往右数第6列。作品二：第20行第6列。作品三：第11行第6列。学生认为，作品一明确了数的方向，不会让人误解。笔者引导学生关注作品二和作品三，并提出质疑。学生结合导演组织排练的情境进行分析，说明第20行第6列的说法没有明确数的方向，可能导致两名学生同时站起来，因此我们要提前规定数的方向。然后，笔者引导学生明确横着的是行、竖着的是列。最后，笔者呈现作品四，即（6，20），引导学生观察这样写是否符合规定。由此，学生发现还需要规定行和列的表示次序，即“先列后行”，这样才能把位置描述清楚。同时，学生发现作品四的表示方法很简洁。

任务二：由数到形，渗透坐标思想。数轴和直角坐标系是数形结合的两个重要模型，本节课的学习要为平面直角坐标系的学习奠定基础。课堂上，笔者先引导学生说一说数对（30，7）描述的演员位置，然后引导学生观察任务二中给出的3组数对，要求学生一边观察每组数对，一边想象数对描述的位置，在格子图中标出相应的点，并说一说有什么发现。学生自主探究后发现：第1组数对所描述的行数依次增加1；第2组数对所描述的列数依次增加1；第3组数对所描述的列数和行数都依次增加1。一名学生补充：第1组数对列数不变，各个点就在同一列上；行数依次加1，点的位置就会在纵向上发生相应变化。笔者提示：数与形紧密关联，一组数对可以表示平面上多个点，连点成线可以形成图形。学生感知这些内容，有助于提高空间想象力，发展空间观念，为后续的数学学习打下基础。

四、设计拓展练习，把握知识本质

教师结合学生熟悉的情境设计多样化的练习，引导学生经历拓展运用的过程，有利于增强学生的推理意识和应用意识。

笔者呈现图3，引导学生谈生活中的数对。

学生发现电影票上的座位信息、一个地点的经度和纬度、国际象棋盘以及动物园各场馆的游览图中都有数对的应用。笔者总结：在之前的学习中，我们在数轴上用一个点表示位置；在本节课学习中，我们从列和行两个维度用数对表示平面上的位置；后续，我们将学习以参照点、方向和距离三个要素确定物体在空间中的位置。

（作者单位：孝感市孝昌县邹岗镇中心小学）

责任编辑  刘佳