基于学习路径分析“分数初步认识”单元主题实践教学

摘  要：“分数初步认识”是在学生已经认识了万以内的整数、理解并掌握了“平均分”意义的基础上开始学习的内容，是学生认识分数的起始课。从整数到分数是数概念的一次扩展，无论在意义、读写方法以及计算方法、比较大小上，分数和整数都有很大的差异。由于分数的意义是学生对整体与部分关系的认识，反映的是一种“关系认识”的思维方式，所以分数概念较之整数概念来说更为抽象。

关键词：学习路径;分数初步认识;单元主题实践

一、单元教材分析

《课程标准（2011年版）》在第一学段课程内容中，明确要求学生“能结合具体情境初步认识分数”，“能比较两个同分母分数的大小”，“会进行同分母分数的加减运算”。根据课程标准的要求和对分数概念理解维度的分析，我们把分数初步认识从单元整体角度进行梳理和分析，建立联系，转化为一个知识网络，既体现了知识间的内在联系，又突出了核心概念，从而发展学生的数学思维能力和问题解决能力，如表1。

二、基于学习路径单元整体研究设想

学习路径的概念一经提出，成为教育研究的一个热点，实施以学习路径为导向的教学，可以促教师的教学有路可寻，有效地实现教学决策，促进学生学习真正理解。本文从假设性学习路径和基于学生认识水平路径来做分析。

实验教师用设计者的身份参与到单元整体结构的设计和每一节课的具体设计中，每个重点课例假设学习路径，制作规划图，优化单元内容结构，体现教学目标与学生发展的层次性：一能设计多样化的学习任务;二能选择合适的教学策略;三能给学生在课堂上提供开放的学习思考空间，如图1。

三、单元整体实践

教材版本：北师大教材

授课年级：三年级

实验学校：陶新小学三（1）班、三（2）班

实验教师评估先期学生学习经验，对学生进行学情分析，了解学生发展起点状态。目前对分一分（一）做了调研，进行了两次试教与反思。

（一）确定三年级下册（分一分）学生学习的起点

在分数的初步认识阶段，学生对分数理解只有“平均分”，在其头脑中痕迹仅有整数和分一分，不认为分数是一个整体，三年级的实验教师对三（1）班43名学生用问卷形式对《分一分》进行先期评估。

1. 前测调研题目及意图，如表2：

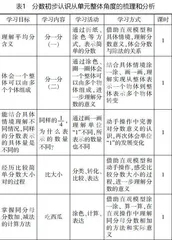
2. 数据分析，如表3：

通过以上对学生前测的分析，我们得出以下结论并提出教学建议。

第一，绝大部分学生不知道什么是“分数”，但是一半以上的学生听说过■这样的具体分数，也知道■表示一半。

第二，有近80%的学生能够正确折出正方形的■，这说明学生能够通过正确的操作得到简单分数。

第三，大部分学生具有平均分的意识并能够正确的平均分，但其中只有部分学生（28%）能够正确使用分数表达分得的结果，部分学生（19%）还是试图用整数来进行表达，没有想到创造一个新数。

由此我们认为，在教学分数初步认识的过程中，要侧重以下几点：首先，要让学生体会分数产生的必要性，当一个整数不能表达的时候，我们需要创造一种新的数来表达;其次，要注重学生在动手操作中，感受平均分对分数意义的影响，进而正确理解分数在具体情境中的意义，即作为“行为的分数”入手来理解分数表示“部分与整体关系”的意义。

（二）分析学习路径

分析学生的学习路径时，除了前测，还需要分析学习路径的方法。①学生在已经掌握除法的基础上理解平均分。②学生对分数的份数定义有不同的表征形式，在教学中，应该使用多种形式对份数意义表征，如文字表征、图形表征、算式表征。还需要让学生用语言进行过渡，实现分数意义的理解。③在教学中应加强对理解过程的重视，从情境到理答，学生从分数与除法关系中，从量入手认识分数，明白分数也能表示商。

（三）两种不同观察策略的试教

经过前测，了解了学生的认识水平后，实验教师进行《分一分（一）》的试教，先后在三1班和三2班进行了两次试教，如表4：

（四）学习路径的最终确定

在前测、试教和相关研究的基础上，最终确定分数份数定义的学习路径：教师通过图形结合、观察比较、交流探讨引导学生：①能找到分的对象是什么？是单个物体多个物体？②知道平均分成几份（分母），取其中的几份？（分子）;③在不同的单位“1”中感受相同或不同的分数，理解分数的无量纲性。④简单分数的大小比较以及加减计算方法，进一步体会几分之几与相关单位分数的内在联系，加深对分数含义的认识。第一、二步是理解分数意义的结构模型，第三、四步进一步让学生建立分数份数定义稳定清晰的认识。

四、设计与实施教学活动

（一）基于学习路径教学活动

根据前面对学生学习路径的分析，在考虑具体的教学任务时，主要设计以下四方面的活动：第一，在具体情境中引导学生观察，积累经验。第二，在操作中揭开分数的本质。第三，在探究活动中丰富分数的认知。第四，在比较分析中表达培养数学思维。这些教学活动实施促进学生对分数份数定义的真正理解。

（二）两次教学后效果反馈（后测）

从分数单元的整体教学思路出发，课堂教学设计不断优化完善，学习路径逐渐清晰，一周后对两个班的学生进行理解水平的后测。

1. 6个苹果平均分给3个人吃，每人吃这些苹果的 （   ），每人吃（  ）个。

2. 三年级（1）班少先队员有5名男生，4名女生，男生占少先队员总数的（   ），女生占少先队员总数的 （   ）。

3. 一袋苹果取了3个，正好取出它的■，这袋苹果原来有（   ）个。

（请同学们在下方写出各题的思考、计算过程）

我们对根据学生具体解答的不同情况与方法，出现了学生解决分数应用能力水平的5个层次的差异，如表6。

从学生课堂表现以及前后测的反馈来看，通过激趣式的导入、教学重难点的重新把握、创新练习的升华，三（2）班学生对于分数意义的理解，较三（1）班都有了很大的提升，为之后分数的进一步学习打下坚实的基础。

（责任编辑：邹宇铭）

参考文献：

[1] 黄荣金，章勤琼，陈锡成. 实施基于学习路径的小学数学教学，促进学生学习和教师成长（上）. 小学教学：数学版，2021（03）：9-12.

[2] 道格拉斯·H.克莱门茨，朱莉·萨拉马. 儿童早期的数学学习与教育——基于学习路径的研究[M]. 张俊，陶莹，李正清，等，译. 北京：教育科学出版社，2020.