立足基础 着力四能 发展素养

［摘 要］文章积极践行初中数学模块化教学理念，以苏科版数学教材八年级下册第9章“中心对称图形——平行四边形”的起始课教学为例，紧扣“中心对称图形”这一大概念，通过巧妙设问、实践操作、师生互动、追问启智、生成思维导图及总结提升等教学活动，使学生获得一般认识、揭示普遍规律、形成系统性思考、领悟数学思想，进而培养其发现问题、提出问题、分析问题和解决问题的能力，发展学生的数学核心素养。

［关键词］初中教学；起始课教学；基础；四能；素养

［中图分类号］    G633.6                ［文献标识码］    A                ［文章编号］    1674-6058（2024）32-0007-03

起始课教学如同景区的导游图，旨在预先展示整章的学习特点、知识结构，并指引研究路径。本文以苏科版数学教材八年级下册第9章“中心对称图形——平行四边形”的起始课为例，构建以“中心对称图形”为大概念的教学设计。通过设计各种实验活动，使学生初步认识什么是中心对称图形，明确什么样的四边形是平行四边形，理解为什么学平行四边形以及怎样学平行四边形。这样的教学为学生的知识体系构建奠定基础。

一、教学设计与分析

（一）巧设问题，自然引入平行四边形

问题1：我们已学过线段、射线、直线、角及三角形等图形，那么接下来还将学习哪些图形呢？

教学分析：学生已在七年级上学期学习了线段、射线、直线和角，并在七年级下学期及八年级上学期学习了三角形。进入八年级下学期，学生将接触学习特殊四边形——平行四边形。平行四边形的学习不仅涉及平行线、三角形及图形变换等知识的综合运用与深化，更为后续学习其他特殊平行四边形奠定基础，并为几何图形的深入学习积累必要的基础知识和基本经验。

追问：三角形和四边形之间存在怎样的关联？能否通过图形变换得到特殊的四边形？

教学分析：四边形并非仅是比三角形多了一条边的简单延伸。在教学中，教师引导学生通过旋转变换图形，揭示三角形与特殊四边形——平行四边形的内在联系。同时，若学生提出“通过沿三角形一边所在直线翻折得到轴对称四边形”的观点，教师应予以肯定，并借此引入“中心对称图形——平行四边形”的对比教学，以加深学生对中心对称的定义及性质的理解。

（二）动手实践，变换形成平行四边形

实践任务：将一个一般三角形绕其一边中点旋转180°。

问题2：你可以发现什么？

教学分析：通过实践操作，学生能直观发现平行四边形与三角形之间的密切联系，为后续深入探究平行四边形的性质奠定基础。问题2通过分类讨论，引出中心对称的概念。

（三）对比思考，初探特殊平行四边形

问题3：三角形具有哪些性质？我们是如何探究这些性质的？你能否通过观察及推理推导出平行四边形的性质？

教学分析：对于三角形，通常研究其边、角和相关的线（如中线、高线）。三角形的性质包括任意两边之和大于第三边；内角和等于180°；一边上的中线可以平分该三角形的面积；高线可用于计算面积；在等腰三角形中，底边上的高线、中线、顶角的角平分线重合；等等。类似地，由三角形旋转[180°]形成的平行四边形，其性质也可从边、角以及对角线等方面进行研究。

追问：若三角形为直角三角形，绕其一边中点旋转180°后，所得的四边形具有什么特征？

教学分析：直角三角形绕其任意一边中点旋转180°后均会得到平行四边形。特别地，若绕斜边中点旋转，所得平行四边形将含有一个直角，从而引出矩形的概念。初时，学生的表达可能还不够完善，因此教师应通过不断引导、补充和追问逐步完善学生的表达，促使其深入思考，进而深化对数学概念的理解和认识。这一过程充分体现了研究数学概念的一般思考方法。

追问：除了直角三角形，还有哪些特殊三角形？它们旋转[180°]后所得的四边形具有什么特征？

教学分析：在探讨三角形与平行四边形的联系时发现，等腰三角形绕其底边中点旋转180[°]后所得平行四边形将有一组邻边相等；等腰直角三角形绕其底边中点旋转180[°]后所得平行四边形不仅是矩形（因为含一个直角），还具有一组邻边相等的特性。由此可自然引出菱形的定义，并在此基础上，顺畅地探究矩形、菱形及正方形的性质。

（四）开放设问，初步判定平行四边形

问题4：如果一个四边形的一组对边平行且相等，那么它是否一定为平行四边形？除此之外，还有哪些条件可以判定一个四边形为平行四边形？

教学分析：此问题为开放性问题，旨在拓展学生思维，让学生认识到除了定义，还有其他多种判定平行四边形的方法。教师应根据实际灵活组织教学，可进一步提问：除了矩形定义中所提及的条件，一个平行四边形在什么条件下是矩形？除了菱形定义中所提及的条件，一个平行四边形还在什么条件下是菱形？本章节涉及的平行四边形、矩形、菱形、正方形的判定方法多达14种，概念之丰富，前所未有。教师应致力于启发学生思维，引导他们运用猜想归纳法，借助逻辑思维从具体实例中发现并总结归纳这些判定方法，从而提升学生分析和解决问题的能力。

（五）埋设伏笔，引导应用平行四边形

问题5：三角形有高线、中线和角平分线，若取任意两边的中点并连接，所得线段具有什么特殊性质？

教学分析：此问题意在引导学生探索三角形中的第四条线——中位线，它有着特殊的位置和数量关系。通过倍长中线法、证明全等或旋转180°证共线等方法，可构造平行四边形，从而提示三角形中位线的性质。新课标亦强调梯形中位线的教学，梯形中位线的探究方法与三角形中位线的探究方法相似，均为构造平行四边形，体现出平行四边形知识的应用价值。对于学生学习中的疑点、当下的困惑及可能面临的挑战，即教学之难点，本节课并不急于一一击破，而是巧妙埋设伏笔，为后续教学奠定基础。

（六）总结收获，绘制思维导图，构建知识网络

问题6：通过本节课的学习，请谈一谈你的收获与困惑，并尝试绘制本章节的思维导图。

教学分析：通过回答此问题，学生能在自主总结的过程中梳理思维脉络，将点状的知识整合为系统的知识网络。这不仅有助于学生巩固所学知识，还有助于提升学生的归纳总结能力。

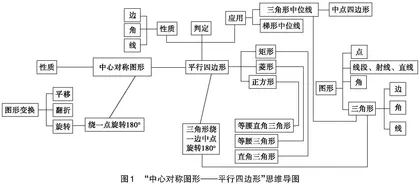
以下展示学生A自主绘制的章节思维导图（见图1）。

思维导图的绘制旨在构建清晰的知识框架，使本章内容一目了然。本节课在系统思维和整体观念的引领下，引导学生绘制“中心对称图形——平行四边形”思维导图，以使学生建立基本知识和思维方法体系。

二、教学反思与展望

数学课堂是思维的课堂，追求思维的深度和广度，最终目标是将复杂的知识简单化，让学生切实掌握学习内容，从而增强学习信心。本节课通过巧妙设问、不断追问、开展灵动对话，不仅巩固了学生的基础知识，培养了学生的基本技能，还使学生深刻领悟了数学思想，并积累了丰富的基本活动经验，取得了显著的学习效果。

（一）立足“基础”，以数学的方法理解问题

本节课基于学生已有的数学基础知识，引导学生运用已学数学方法理解并解决问题，增添课堂趣味。学生已掌握一般三角形与特殊三角形的定义及性质；而平行四边形的定义、性质、判定等为本节课的核心内容。为实现这两个知识模块的有机整合，笔者巧妙设问，引导学生通过旋转变换三角形，探索更复杂的图形——平行四边形。这样的教学设计能有效激发学生的探究兴趣，促进知识的自然建构。

（二）着力“四能”，运用数学思想解决问题

本节课着力“四能”的培养，即通过6个问题的逐一解决，着重培养学生发现问题、提出问题、分析问题和解决问题的能力。在教学中，笔者引导学生观察、思考与表达，培养学生的合作能力、总结能力和提问能力，还鼓励学生勇于质疑、乐于探索，使课堂成为学生自主发现的舞台。学生在探究平行四边形、矩形、菱形、正方形等图形的过程中，运用分类讨论、对比等数学思想方法，自主获取数学知识，学习数学方法，领悟数学思想，从而实现关键能力的发展。

（三）发展“素养”，以数学思维激发创新

本节课作为章节起始课，旨在构建基本知识框架。通过引导学生绘制章节思维导图，鼓励他们主动总结收获并提出疑问，从而发展学生的核心素养。在交流环节，学生可能会尝试探究由三角形三边中点连接而成的小三角形，或是探究连接一般四边形四边中点后形成的图形，这些自发的创新行为都应予以肯定。

本节课的核心任务是挖掘单元“大概念”，重组学习“大任务”，基于数学核心素养的落实要求进行知识梳理，为后续教学提供纲领性指导。

在今后的数学课堂教学中，笔者将持续深入研读课标，深度挖掘教材，精准把握起始课的教学价值，构建以“大概念”为核心的初中数学起始课结构化教学体系，切实推进数学核心素养的落实。

［   参   考   文   献   ］

[1]  周利明.在认知关联处提升数学思维：以“平行四边形及其性质”教学为例[J].中学数学教学参考，2023（32）：12-14.

[2]  董文峰，任宏章.活用情境，巧设问题，生成发展[J].中学数学，2023（20）：14-17.

[3]  王海珠.猜想归纳方法在初中数学学习中的应用策略[J].数理化解题研究，2023（35）：56-58.

[4]  安文华.埋伏笔于情境   化难点于无形：也谈“函数[y=Asin（ωx+φ）]的性质与图象”[J].数学通报，2022（8）：30-32，45.

[5]  朱佳炜，任宏章.活用思维导图   助力微课生长：以“二次函数的图象、性质与系数的关系”微专题教学设计为例[J].中学数学月刊，2022（8）：15-16，22.

[6]  宋健.观念、任务与进阶：数学单元课时教学的着力点：以苏教版“圆锥曲线与方程”为例[J].天津师范大学学报（基础教育版），2023（2）：39-42.

[7]  孙家和.单元视野下“大概念”的建构与实施：以“3.2函数的基本性质”教学为例[J].中学数学教学参考，2023（13）：66-68.