玩转数独，感受数学好玩

［摘 要］数学课堂中，为了让学生感受数学好玩，以数独游戏为例开展教学：通过玩转基本数独，帮助学生了解游戏规则；通过玩转不等号数独，帮助学生感悟数的大小关系；通过玩转加法数独，帮助学生习得数学思想方法；通过玩转肯肯数独，帮助学生挑战自我极限。这样教学，有助于学生学会如何用理性的眼光去观察世界，用逻辑的思维去分析问题，用创新的方法去解决问题。

［关键词］数独；基本数独；不等号数独；肯肯数独

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）06-0018-03

著名数学家陈省身提出“数学好玩”，强调数学不仅有公式和定理，更是一个充满乐趣、创造性和无限可能性的奇妙世界。数独游戏，完美诠释了陈省身先生提出的“数学好玩”的精髓。它既是一款简单的数字填充游戏，也是锻炼逻辑思维、提升专注力、培养解决问题能力的绝佳工具。因此，将数独游戏引入小学数学课堂，不仅是对陈省身先生“数学好玩”理念的具体实践，还是促进学生全面发展、提升学生数学素养的有效途径。这样有助于教师鼓励学生勇于对数学现象等提出疑问，探究数学知识的奥秘，体验解决问题的喜悦与成就感。

一、玩转基本数独，了解游戏规则

基本数独是一款经典的数字逻辑推理游戏，其玩法简单而富有挑战性，即在一个9×9的网格中填入1～9的数字，要求每行、每列以及每个3×3的子网格中的数字都不能重复。在这个过程中，玩家需要根据格子中已有数字的提示，利用逻辑推理和排除法，逐步填入剩余的数字。随着经验的积累和实践的深入，玩家还可以尝试挑战更高难度的数独游戏。

【教学片段】

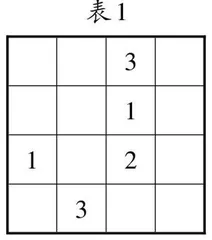
师：同学们，我们已经知道了四宫格数独游戏的规则。（出示表1）想一想，这个数独的突破口在哪里？

生1：我们把表格中横的叫作行，从上到下分别是第1行、第2行、第3行和第4行；把竖的叫作列，从左到右分别是第1列、第2列、第3列、第4列。这个数独的突破口是第3列的第4行，行已经有3，列已经有1、2、3，所以第3列的第4行一定是4。

师：大家听懂了吗？根据这个表中已经知道的数，就能确定空格里的数。剩下的空格，大家试一试吧！

生2：我们看第4行的第1列，行已经有3和4， 列已经有1， 所以这里一定是2；第4行已经有2、3、4，故第4行的第4列一定是1；看第3行的第2列，行已经有1和2，列已经有3，所以这里一定是4；第3行已经有1、2、4，故第3行的第4列一定是3；看第1行的第1列，行已经有3，列已经有1和2，所以这里一定是4；第1列已经有1、2、4，故第1列的第2行一定是3；看第2行的第2列，行已经有1和3，列已经有3和4，所以这里一定是2；第2列已经有2、3、4，故第2列的第1行一定是1；第1行已经有1、3、4，所以第1行的第4列一定是2；最后看第4列，已经有1、2、3，所以第4列的第2行一定是4（见表2）。填数完毕之后检查一下，由于每行都有1～4，每列都有1～4，所以这个数独是正确的。

师：这位同学非常完整又清晰地向我们展示了解决数独的思路：先根据每行和每列已有的数字，再确定未知空格里的数字，最后还要仔细检查一下每行和每列是否每个数字只出现一次。

……

上述教学，教师以引导者和启发者的身份，巧妙地开展了一系列活动，带领学生逐步深入探究基本数独的奥秘，共同经历了一场充满挑战与乐趣的探究之旅。首先，教师展示一个部分填充的数独游戏，并讲述数独的历史背景，迅速吸引学生的注意力。接着，教师详细讲解数独的基本规则并进行提问，确保每位学生都能准确掌握数独的规则。在讲解规则后，教师组织学生开始进行数独的探究实践，引导学生一步步进行推理和填数。在这个过程中，教师鼓励学生大胆尝试，即使犯错也不要紧，重要的是从错误中学习并调整策略。最后，教师组织全班学生总结归纳。学生纷纷分享了自己在解题过程中的心得体会，并提炼出解决数独的几个关键步骤和常用方法。

二、玩转不等号数独，感悟大小关系

不等号数独是在传统数独的基础上，增加了数字大小关系约束的数独游戏。这种数独游戏不仅要求玩家在每行、每列以及每一个3×3的宫格内填入1～9的数字，而且每个数字必须仅出现一次，同时还要满足额外的条件——特定格子间的数字必须满足一定的大小关系。在玩不等号数独的过程中，学生既要进行细致的观察和逻辑推理，又要灵活运用各种策略和技巧来解决问题，感受数学的秩序美和逻辑美。

【教学片段】

师：同学们，这节课我们来研究不等号数独。不等号数独，既要遵循每行和每列都要有1～4这四个数字的规则，又要根据大于号和小于号来确定具体数字的位置。（出示表3）我们一起来看看这个不等号数独，你会先确定哪些数字？

生1：先看第1行，因为行中已经有3，还有2个小于号，告诉我们最右边的数最大，所以第1行的第2列是1，第3列是2，第4列是4。

师：我们来检查一下第1行，看看1～4这四个数字是否都只出现了一次。（是）是否符合这样的不等关系？（是）接着看第4列，自己先在学习单上试一试，再和同桌说一说是怎么想的。

生2：第4列已经有4，且2个小于号告诉我们最下面的数最大，所以第4列的第2行是1，第3行是2，第4行是3。

师：现在我们来检查一下第4列，看看1～4这四个数字是否都只出现了一次。（是）是否符合这样的不等关系？（是）接下来看第4行，相信你们一定能挑战成功！

生3：第4行已经有3了，且大于号告诉我们最左边的数最大，所以第4行的第1列是4，第2列是2，第3列是1。

……

上述教学，教师先向学生展示一个基本数独的示例，简要回顾其基本规则，并以此作为新知识的引入，再出示一个更有趣、更具挑战性的不等号数独，激发学生的好奇心。接着，教师利用多媒体向学生介绍不等号数独的独特之处：除了要满足基本数独的规则，还要根据宫格中给出的不等号来确定数字的大小关系。这个数独游戏不仅考验玩家的逻辑思维，还融入数学中的不等式概念，使数独游戏变得更加丰富和有趣。为了让学生更好地理解不等号数独的玩法，教师引导学生观察宫格中已知的数字和不等号，并示范如何利用这些线索进行推理。在学生对不等号数独有了初步了解后，教师放手让他们独立尝试解决，并展示他们的解题成果和心得体会。

三、玩转加法数独，渗透思想方法

加法数独要求玩家在规定的空格内填入数字，使得每行、每列以及特定区域内的数字之和等于给定的目标值。玩转加法数独是一个既有趣，又有挑战性的过程。通过数形结合、逻辑推理、排除法、假设法等方法的应用，以及观察分析、优先填充和验证检查等策略的运用，确保填入数字的准确性和效率，提高学生的逻辑思维能力、数学素养。

【教学片段】

师：（出示表4）同学们，这是一个加法数独。六宫加法数独的游戏规则是在空格里填入1～6数字，使得每行、每列及每个宫格内的数字都不重复；宫格中的提示数字，表示相邻两格的数字之和。比如，第1列中的提示数字“5”，意思是说第1列的第1行和第2行这两个数字相加要等于5。请同学们先在学习单上试一试，再想一想应从哪个提示数字入手。

生1：我会先从“3”这个提示数字入手，因为第3行已经有2了，而且只有1+2=3和2+1=3，所以第3行的第4列一定是1，第2行的第4列一定是2。

师：你根据“3”这个提示数字，一下子确定了两个空格。现在表中的右上角已经有四个已知数字了，想一想怎么破解剩下的空格？

生2：表中的右上角有一个提示数字“7”，由于右上角已经有1和6，所以只要考虑3+4=7和4+3=7这两种情况。这样，第1行的第4列可能是1或5，由于第3行已经有1，所以第1行的第4列只能是5，第6列一定是1。我还能根据提示数字“11”，确定右下角的数字。因为只有5+6=11，但是第6行已经有6了，所以第6行的第6列一定是5……

上述教学中的加法数独，既要考虑数字不能重复，又涉及加法运算。因此，教师引导学生先把

1～6中的每两个数字相加，再按照和的大小进行分类，也可以按照组合数量进行分类。这样在解决加法数独时，就可以先利用一种组合把能确定的空格先确定，再利用2种组合或3种组合排除不可能的数字，从而确定其他空格中的数字。

四、玩转肯肯数独，挑战自我极限

肯肯数独比普通数独更具有挑战性，因为每个宫格或一组宫格不仅要满足“每行、每列和每个宫格内数字不重复”的规则，还要根据给出的加法、减法、乘法、除法等运算来得到指定的结果。另外，肯肯数独需要时间和耐心来逐步解开谜题，不能急于求成，以享受解题过程中的乐趣和成就感。

【教学片段】

师：（出示表5）同学们，这是一个肯肯数独。肯肯数独比加法数独多了减法、乘法和除法等运算。比如，写着“2÷”，表示这两个空格里的数相除要等于2；写着“6×”，表示这两个空格里的数相乘要等于6。下面，大家试一试这个3×3的肯肯数独吧！

生1：这个数独中第3行的第1列的提示数字是“3”，所以第3行的第1列一定是3。第2行的第2列的提示是“2÷”，只有2÷1=2；又因为第1行的第2列的提示是“6×”，只有2×3=6，这样就能确定第1行的第2列是3，第1行的第3列是2，第1行的第1列是1。第1行的第1列的提示是“3+”，只有1+2=3，所以第2行的第1列是2，这样第2行的第2列只能是1，第3行的第2列只能是2。因此，第2行的第3列是3，第3行的第3列是1。

师：填完数之后，我们检查一下，每一行和每一列中1～3这三个数字是否都只出现了一次？（是）是否符合这样的不等关系？（是）

……

上述教学，为了让学生更直观地感受肯肯数独的魅力，教师出示简单的肯肯数独，既包含基本的数学运算，又兼顾了游戏的趣味性，意在让学生轻松上手，更加喜欢上数学学习。在分享讨论环节，有的学生讲述了自己在解题过程中遇到的困难和挑战，有的学生则分享了自己独特的解题思路和策略，让其他学生受益匪浅，进一步激发了学生对数独的兴趣和热情。

在深入探索数独游戏的教学价值中，我们发现它不仅仅是一个个格子与数字的简单组合，还蕴含着严密的逻辑推理、灵活的策略以及坚持不懈的毅力。每一次的探究，都是对自我极限的一次挑战；每一次挑战成功，都是对智力与耐心的一次考验。这样引入游戏开展数学教学，数学不再是书本上冰冷的公式和定理，而是化身为生动有趣的游戏，激发学生对未知世界的好奇心和探索欲，教会学生如何用理性的眼光去观察世界，用逻辑的思维去分析问题，用创新的方法去解决问题。

（责编 杜 华）