基于代数几何，培养推理意识

［摘 要］《义务教育数学课程标准（2022年版）》对“三角形的三边关系”这一内容的教学，提出了新的方向和要求。基于此，教师要在已有经验的基础上寻求突破，结合尺规作图、代数思维、推理意识三个方面，进行新的教学尝试，使学生的思维水平在几何作图中得到提升，实现发展学生数学核心素养的目标。

［关键词］尺规作图；代数思维；推理意识；磨课

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）36-0014-04

“三角形的三边关系”是苏教版数学教材四年级下册内容，旨在引导学生通过观察、猜想、操作和分析等活动，自主探索和发现三角形的三边关系。《义务教育数学课程标准（2022年版）》（以下简称“数学新课标”）在这一内容中增加了尺规作图探索三角形三边关系和运用几何基本事实进行推理的教学提示。这就意味着教师要思考如何借助尺规来设计探究活动，使学生能够基于几何作图，对发现的数学规律进行探究和表达，从而突破认知难点。同时，教师要注重引导学生经历推理的过程，明白规律背后的道理，能够基于推理掌握尺规作图的方法。

基于以上思考，我尝试在“三角形的三边关系”这一内容教学中融入代数思维，引导学生借助尺规作图进行新的操作实验，加强学生对规律的推理，培养学生的推理意识，提升学生的数学核心素养。

一、问题相同，活动不同

片段（一）：按照教材，尝试运用小棒进行探究

师：任意3根小棒都能围成三角形吗？（出示长度为3cm、4cm、5cm、8cm的4根小棒）老师为大家准备了4根小棒，现在请同学们先按要求围一围，再展示汇报。（多媒体出示活动目的和要求）

活动目的：借助小棒探究三角形的三边关系。

活动要求：（1）选一选。4人小组，每人选择不同的3根小棒。（2）围一围。用小棒围一围三角形，并记录结果。（3）说一说。小组内相互说说操作过程和结果。

师：哪些小棒能围成三角形，哪些小棒不能围成三角形？

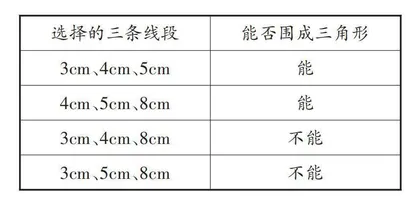
生1：能围成三角形的3根小棒有3cm、4cm、5cm，4cm、5cm、8cm，3cm、5cm、8cm；不能围成三角形的三根小棒是3cm、4cm、8cm。

师：同学们得到的结果一样吗？

生2：结果一样。

生3：可我用3cm、5cm、8cm这3根小棒不能围成三角形。

师：我们再来用这3根小棒围一围，看能不能围成三角形。

片段（二）：基于课标，熟练运用尺规探索规律

师：（出示长度为3cm、4cm、5cm、8cm的4条线段）这里，任意的3条线段都能围成三角形吗？（学生猜想）有了猜想，就要进行验证。你们想怎么进行验证？

生4：画一画，看看能不能围成三角形。（教师通过多媒体出示活动目的和要求）

活动目的：借助尺规作图探究三角形的三边关系。

活动要求：（1）选一选。4人小组，每人选择不同的3条线段。（2）画一画。借助直尺和圆规画三角形，保留作图痕迹。（3）说一说。说说能围成或不能围成三角形的原因。

生5：不能围成三角形的线段有3cm、4cm、8cm和3cm、5cm、8cm，能围成三角形的线段有3cm、4cm、5cm和4cm、5cm、8cm。

【思考】教材为本课教学提供的材料是小棒，让学生通过小棒围三角形的操作活动，探究三角形的三边关系。但在实际教学过程中往往会出现问题，因为小棒较粗，操作中易出现误差，不利于学生发现和总结规律。为了使探究过程更严谨和更科学，我结合数学新课标中的教学要求，尝试借助尺规作图来设计操作活动。

借助尺规画三角形，是在画等长线段的基础上，先找到三角形的第三个顶点，再画出三角形，让学生感受由一维空间到二维空间的发展。运用尺规作图探究三角形的三边关系，要求学生灵活运用尺规，并结合作图过程进行推理，这是学生对尺规作图的深化应用。其意义不仅在于让学生明确尺规作图的价值，感悟数学的严谨性，更在于让学生熟练运用并进行推理，培养学生的推理意识。

二、教材相同，思维不同

片段（一）：依照教材，展现常规教学思路

师：任意3条线段都能围成三角形吗？（多媒体出示活动目和要求）

活动目的：借助尺规作图探究三角形的三边关系。

活动要求：（1）选一选。在长度为3cm、4cm、5cm、8cm的线段中，任选3条不同的线段。（2）画一画。借助直尺和圆规画三角形，保留作图痕迹，并标明数据。（3）说一说。说说能围成三角形或不能围成三角形的原因。

生1：长度为3cm、4cm、8cm和3cm、5cm、8cm的两组线段不能围成三角形。

师：为什么不能围成三角形？每组的3条线段有怎样的关系？

生2：因为3+4<8或3+5=8，所以不能围成三角形。

生3：长度为3cm、4cm、5cm和4cm、5cm、8cm的两组线段能围成三角形。

师：为什么能围成三角形？每组的3条线段有怎样的关系？

生4：因为3+4>5、4+5>8，所以它们能围成三角形。

师：观察思考，能围成三角形的3条线段有怎样的关系？（学生回答略）

师生小结：能围成三角形的3条线段，其中2条较短线段的长度的和大于最长的线段。

片段（二）：开发教材，促进代数思维发展

师：任意的3条线段都能围成三角形吗？（多媒体出示活动目的和要求）

活动目的：借助尺规作图探究三角形的三边关系。

活动要求：（1）选一选。4人小组，每人从a、b、c、d这4条线段（实际长度为3cm、5cm、8cm、4cm）中，任选3条不同的线段。（2）画一画。借助尺规画三角形，保留作图痕迹。（3）说一说。说说能围成三角形或不能围成三角形的原因。

生5：不能围成三角形的线段有a、b、c和a、c、d。

师：它们为什么不能围成三角形？

生6：两条线段没有交点，或交点在线段c上。

师：这个交点就是什么？

生7：三角形的第三个顶点。

师：这3条线段有什么关系？

生8：a+b=c，a+d<c。

师生小结：不能围成三角形的3条线段，其中2条线段的长度和小于或等于第3条线段。

生9：能围成三角形的线段有a、b、d和b、c、d。

师：它们之间有什么关系？

生10：a+d>b，b+d>c。

师生小结：能围成三角形的3条线段，其中2条线段的长度和大于第3条线段。

师：观察并想一想，能围成三角形和不能围成三角形的情况有何不同？（学生回答略）

师生小结：能围成三角形的3条线段有交点且在线段外，不能围成三角形的3条线段没有交点或交点在线段上；能围成三角形的任意2条线段长度的和大于第3条线段，不能围成三角形的任意2条线段长度的和等于或小于第3条线段。

师：任意2条线段长度的和大于第3条线段，就一定能围成三角形吗？（多媒体出示活动目的和要求）

活动目的：突破“任意”。

活动要求：（1）选一选。在能围成三角形的3条线段中，除最长的线段，任选一条线段为底边。（2）画一画。借助尺规画三角形，保留作图痕迹。（3）说一说。说说能不能围成三角形和3条线段的关系。

师：你以哪条线段为底？能围成三角形吗？这3条线段有什么关系？（学生回答略）

师：分别以这3条线段为底，画出3个三角形，观察一下，它们有什么关系？（学生操作略）

师生小结：任意2条线段长度的和大于第3条线段，这样的3条线段能围成三角形。

【思考】借助尺规作图来探究三角形三边关系的教学，旨在通过几何直观和数形结合的方式，让学生能更直观、更清楚地发现三角形的三边关系，得到初步的结论。但这样的教学设计也存在以下问题：一是学生在运用尺规作图之后，没有利用好直观图示去观察、发现三角形的三边关系，更多的还是停留在计算三边的长度上，也就失去了运用尺规作图的意义和价值；二是教材提供4条指定数据的线段，得到的结论不具有一般性。因此，教师要在此基础上深入钻研教材和数学新课标，进行新的教学尝试，寻求突破。

我尝试将代数思维融入教学之中，即将教材中明确长度的4条线段换成与之等长的a、b、c、d这4条线段。课堂上，先让学生根据核心问题提出猜想，再展开操作活动，并用含有字母的式子来表示三角形的三边关系，促使学生的算术思维向代数思维转化。同时，借助尺规作图，学生能总结出围成和不能围成三角形的三边关系，进一步探究能围成三角形的三边关系，最后得出三角形三边关系的一般性结论。课堂上，学生多次尝试运用代数思维进行表达，并结合尺规作图进行推理，使自身的代数思维得到发展。代数思维作为数学核心素养的重要体现，教师要有意识地对学生进行培养，深化学生对数学本质的理解。

三、规律相同，方法不同

片段（一）：列举验证，论证三边关系

1.操作发现

师：（出示上表）观察计算并想一想，能围成三角形的3条线段有怎样的关系？

师：所有的三角形，任意两边长度的和都大于第三边吗？

2.画图验证

活动目的：验证三角形的三边关系。

活动要求：（1）画一画。借助尺规，随意画三角形。（2）量一量。量出三角形的三边长度。（3）算一算。计算三角形的三边长度是否符合规律。

片段（二）：推理验证，强化推理意识

1.反证规律

师：这里，“任意”两个字能去掉吗？对于不能围成三角形的3条线段，你能完整地说说这3条线段之间的关系吗？

生1：a+c>b，b+c>a或a+c>d，d+c>a。

师：现在没画图，你是怎么确定a+c>b、b+c>a的？

生2：最长的线段加上其中一条较短的线段，一定大于另一条较短的线段。

师：看来，我们还能通过推理得到三角形三边的另外两种关系。可这里也有两条线段长度的和大于第三条线段，为什么也不能围成三角形？（学生回答略）

师生小结：三角形中，只要有两条线段长度的和不大于第三条线段，就不符合结论，即不能围成三角形。

2.数据论证（几何画板）

师：所有的三角形都有这样的三边关系吗？老师随意画一个三角形，从数据看，它的三边关系符合这个结论吗？

师：（运用多媒体，随意拖动顶点）从数据看，它的三边关系变化了吗？

师生小结：不管三角形怎么变化，它的三边关系始终不变。

3.方法优化

师：（出示2、5、6，2、4、6，2、2、5这三组线段）判断每组的3条线段能否围成三角形，并说明理由。

师：如果是3条不同的线段a、b、c呢？2条相同的线段a和一条线段c呢？3条相同的线段a、a、a呢？（多媒体出示图1）

4.演绎推理，论证归纳

师：（出示图2）蚂蚁想吃这块蛋糕，该选哪条路？你想到了以前学过的什么知识？

师：你能用“两点之间线段最短”这一知识点来解释三角形的三边关系吗？

师：把三角形三边的三个关系合并成一句话，就是今天学习的什么？

……

【思考】常规教学中，教师先引导学生对任选3根小棒围三角形的不同情况一一列举并观察分析，得出初步的结论后，再验证是不是所有的三角形都符合这一结论。这样设计是通过举例、计算来验证结论的，缺乏推理。因此，教师要设计不同的推理验证环节，加强对学生推理意识的培养。

首先，在学生得出初步的结论后，通过问题“这里，‘任意’两个字能去掉吗”，引导学生聚焦不能围成三角形的情况，以代数推理反证三角形的三边关系。其次，运用几何画板，引导学生发现所有三角形都符合这样的三边关系，从代数推理到数据验证，再一次验证结论。在学生讨论交流后增加一个方法优化环节，即让学生掌握判断是否能围成三角形的最优方法。此环节，列举了一般三角形、等腰三角形和等边三角形的所有情况，即从特殊到一般进行代数推理。最后，创设蚂蚁吃蛋糕的情境，让学生联系旧知进行推理分析，又一次验证结论的正确性，明白研究要有据可证。

本节课教学基于代数几何，引导学生体会用字母表达式来概括三角形的三边关系，感悟规律的一般性。同时，尺规作图作为本节课学生学习的有力抓手，能使探究过程有图可见，并通过代数推理，促使学生的思维从直观思维向抽象思维发展。学生在作图操作中经历想象、分析、推理等思维过程，直观的几何图示已然成为学生推理意识形成和发展的助推器，使学生深刻理解了所学的数学知识，几何直观和推理意识也得到了发展。整堂课，通过几何直观和数形结合的方式进行教学，不仅为学生用字母式表示三角形的三边关系提供了直观依据，还为借助算术方法验证代数概念提供了载体，获得了较好的教学效果。

［ 参 考 文 献 ］

[1] 王建芹，章莉.尺规作图，让学生思有源、推有据：“三角形的三边关系”教学实践与思考[J].小学教学（数学版），2024（4）：42-46.

[2] 包蓉.借助尺规作图探究三角形的三边关系[J].小学教学设计，2024（17）：51.

（责编 杜 华）