新证完全非弹性碰撞机械能损失最大

摘   要：一维碰撞时完全非弹性碰撞的机械能损失是最大的，给出构造动能圆和动量线的几何方法以及利用柯西不等式的代数方法这两种全新的证明方法。

关键词：动能圆；动量线；柯西不等式；完全非弹性碰撞

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2025）2-0074-2

一维碰撞是高中物理重要的力学模型之一。碰撞中如果机械能守恒称为弹性碰撞，如果机械能减少则为非弹性碰撞。当两物体碰后速度相同时，称为完全非弹性碰撞，此时损失的机械能最大。为何完全非弹性碰撞损失的机械能最大呢？证明的方法有很多，如陈坤老师利用导数求解极值法，将两体一维碰撞等效为物块在凹槽中运动的等效模型法，利用大学物理柯尼希定理证明的推论法［１］；廖秀秀老师利用动量守恒，配出动量项的配项法，利用二次方程有解的判别式法［２］；王金聚老师利用基本不等式求解极值的不等式法［３］。针对这一问题，下面给出两种全新的证明方法。

１    几何法

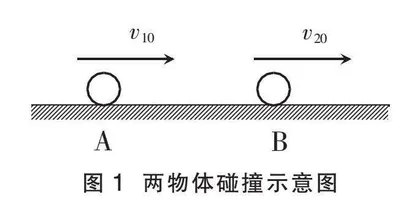
如图１所示，质量分别为ｍ１和ｍ２、半径相同的两个小球Ａ和Ｂ在同一光滑水平面上向右运动。Ａ、Ｂ的速度分别是ｖ１０ 和ｖ２０，且满足ｖ１０＞ｖ２０。某时刻发生碰撞，碰后Ａ、Ｂ的速度分别是ｖ１和ｖ２。

设系统碰后的末动能

Ｅ＝mv+mv（１）

令Ｅ＝x2+y2

其中，x=v，y=v

则系统的末动量

p=mv+mv=x+y

因碰撞过程中动量守恒，则p为常数，为此x、y之间满足线性关系。作出y-x的函数图像如图２所示，称此直线为动量线，直线斜率kp=-。x，y满足方程（１），则（x，y）在以（０，０）为圆心、半径为的圆上，此圆称为动能圆，如图２所示。

要使碰撞过程有解，则动量线和动能圆应有交点。因碰撞过程中动量守恒，动量线的斜率和截距都唯一确定。碰后机械能损失最大，应使得碰后动能最小，即动能圆半径应最小。当动能圆与动量线相切时，动能圆半径最小。切点满足

×k=-1

代入斜率计算可知，满足v2=v1。

点评 此方法构思巧妙，利用了解析几何的方法，通过建立直角坐标系，作出“动能圆”与“动量线”，将抽象的代数问题转化为形象直观的几何问题，可激发学生的学习积极性，提升数理结合的素养。

２    代数法

上述的几何方法虽能证明两物体碰撞时完全非弹性碰撞机械能损失最大，但在处理多物体碰撞问题时，利用此方法却不易处理。下面给出利用柯西不等式的证明方法。柯西不等式如下：

（a+a+…+a）（b+b+…+b）≥（ab+ab+…+ab）

当==…=时，不等式取等号。

如图３所示，有多个小球在同一光滑水平面上向右运动，某段时间内，小球间发生相互碰撞。

利用柯西不等式可知，系统的末动能、末动量、总质量满足

（mv+mv+…+mv）（m+m+…+m）≥（mv+mv+…+mv）

系统碰后动能的一半满足

（mv+mv+…+mv）≥

p表示系统碰后的末动量，满足

p=m1v1+m2v2+…+mnvn

根据柯西不等式，当==…=，即v=v=…=vn时，不等式取等号，碰后系统动能最小，得证。

点评  柯西不等式是高中数学要求学习的重要不等式。利用柯西不等式证明该物理问题不仅简明快捷，而且可以让学生经历运用数学思想与方法来表述物理概念，描述物理规律，解决物理问题，对于提升科学思维和解决物理问题的能力大有裨益。

３    结  论

近年来，高考中不断出现利用解析几何、不等式解决物理问题的试题，比如２０２１年浙江高考第２１题第３问用到均值不等式，２０２２年重庆高考第１４题第２问求解虫在ｘ轴上飞出的位置范围用到解析几何，２０２３年湖南高考第１５题第２问求解小球的轨迹方程用到解析几何。在平时的课堂教学中注意渗透解析几何和不等式解决物理问题这一想法，有利于提升学生的数理结合素养。

参考文献：

［１］陈坤．巧证完全非弹性碰撞中系统动能损失最大［Ｊ］．物理教师，２００９，３０（１）：１２．

［２］廖秀秀．完全非弹性碰撞机械能损失最大的四种推导方法［Ｊ］．中学物理教学参考，２０２３，５２（３５）：６２－６４．

［３］王金聚．为什么说完全非弹性碰撞中损失的动能最多？［Ｊ］．物理教学探讨，２０１９，３７（３）：６３－６４．

（栏目编辑    蒋小平）