巧用动量定理求解电磁感应综合问题

摘   要：金属棒切割磁感线运动问题是高考物理电磁感应综合应用中的一类典型题目。从2022年三道高考题入手，按照单杆、双杆、方框三种模型进行分类探析，利用动量定理对各种模型在非匀变速直线运动过程中的位移和电荷量进行定量求解。

关键词：高考物理；电磁感应；动量定理

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2024）1-0049-3

金属棒切割磁感线运动模型是电磁感应综合应用的一类典型问题，在历年高考中出现频率很高，重点考查运动与相互作用观念、能量观念等要素［１］，难点在法拉第电磁感应定律、闭合电路欧姆定律与牛顿运动定律、功能关系相结合。按照研究对象的种类，可分为单杆、双杆、方框三种模型，接下来逐一进行分析。

1    单杆模型

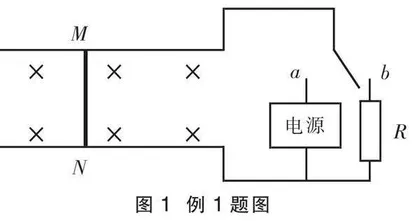
例1 （2022年海南高考物理第18题）如图1所示，光滑的水平长直轨道放在匀强磁场B=0.25 T中，轨道宽0.4 m，一导体棒长也为0.4 m，质量为0.1 kg，电阻r=0.05 Ω，它与导轨接触良好。当开关与a接通时，电源可提供恒定的1 A电流，电流方向可根据需要进行改变，开关与b接通时，电阻R=0.05 Ω，若开关的切换与电流的换向均可在瞬间完成，求：

（1）当棒中电流由M流向N时，棒的加速度的大小和方向是怎样的；

（2）当开关始终接a，要想在最短时间内使棒向左移动4 m而静止，则棒的最大速度是多少；

（3）要想棒在最短时间内向左移动7 m而静止，则棒中产生的焦耳热是多少。

解析 （1）当导体棒中电流由M流向N时，只受安培力的作用，大小为F=BIL=0.1 N，方向为水平向右，因此棒的加速度大小为a=F/m=1 m/s2，方向为水平向右。

（2）当开关始终接a时，导体棒向左只有两种运动情形，一是匀加速运动（电流由N流向M），二是匀减速运动（电流由M流向N）。要想在最短时间内使棒向左移动s=4 m而静止，只能先做初速度为0的匀加速运动，达到最大速度vm后做匀减速运动至静止，两个阶段加速度的大小均为1 m/s2。由匀变速直线运动公式可知，v2m=2a1s1=2a2s2，s1+s2=s，联立解得vm=2 m/s。

（3）当开关接b且导体棒向左运动时，棒切割磁感线会产生感应电动势ε=BLv，并在回路中形成感应电流I3=ε/（R+r），棒所受安培力F3=BI3L=B2L2v/（R+r），方向向右，加速度的大小a3=F3/m=v（SI），即棒做加速度减小的变减速运动。当棒的速度大于1 m/s时，加速度a3>a2；当棒的速度小于1 m/s时，加速度a3<a2。

由于棒在减速阶段有两种方式，因此要想棒在最短时间内向左移动s=7 m而静止，在减速阶段必须选取加速度大的减速方式，即先做初速度为0的匀加速运动（开关接a，电流由N流向M），达到最大速度v3后，先做变减速运动（开关接b）至速度为v4=1 m/s，再做匀减速运动（开关接a，电流由M流向N）至静止。由匀变速直线运动公式可知，。

对于变减速运动阶段的位移s4，我们无法使用运动学公式，但可以利用动量定理进行计算。

点评 对于双杆模型，如果双杆均在磁场区域运动，那么双杆均产生感应电动势，若双杆不受外力作用，则在运动方向上遵循动量守恒定律。如果其中一杆离开磁场区域，那么只有另一杆会产生感应电动势且受到安培力的作用。

3    方框模型

例3 （2022年1月浙江选考物理第22题）如图3所示，水平固定一半径r=0.2 m的金属圆环，长均为r、电阻均为R0的两金属棒沿直径放置，其中一端与圆环接触良好，另一端固定在过圆心的导电竖直转轴OO′上，并随轴以角速度ω=600 rad/s匀速转动，圆环内左半圆均存在磁感应强度大小为B1的匀强磁场。圆环边缘、与转轴良好接触的电刷分别与间距l1的水平放置的平行金属轨道相连，轨道间接有电容C=0.09 F的电容器，通过单刀双掷开关S可分别与接线柱1，2相连。电容器左侧宽度也为l1、长度为l2、磁感应强度大小为B2的匀强磁场区域，在磁场区域内靠近左侧边缘处垂直轨道放置金属棒ab，磁场区域外有间距也为l1的绝缘轨道与金属轨道平滑连接，在绝缘轨道的水平段上放置“［”形金属框fcde。棒ab长度和“［”形框的宽度也均为l1，质量均为m=0.01 kg，de与cf长度均为l3=0.08 m。已知l1=0.25 m，l2=0.068 m，B1=B2=1 T，方向均为竖直向上；棒ab和“［”形框的cd边的电阻均为R=0.1 Ω，除已给电阻外其他电阻不计，轨道均光滑，棒ab与轨道接触良好且运动过程中始终与轨道垂直。开始时开关S和接线柱1接通，待电容器充电完毕后，将S从1拨到2，电容器放电，棒ab被弹出磁场后与“［”形框粘在一起形成闭合框abcd，此时将S与2断开，已知框abcd在倾斜轨道上重心上升0.2 m后返回进入磁场。

（1）求电容器充电完毕后所带的电荷量Q，哪个极板（M或N）带正电？

（2）求电容器释放的电荷量ΔQ；

（3）求框abcd进入磁场后，ab边与磁场区域左边界的最大距离x。

匀速运动的位移x2=l3-l2=0.012 m。

因此，距离x=x1+x2=0.14 m。

点评 对于方框模型，在速度方向垂直于磁场边界的情况下，进入磁场后只有完全进入磁场的那条边产生感应电动势。若磁场区域无限大，则方框全部进入磁场后便不再产生感应电动势；若磁场宽度大于方框宽度，则方框全部处于磁场期间不产生感应电动势，当方框一边出磁场后，在磁场中的那条边会产生感应电动势；若磁场宽度小于方框宽度，则进入磁场的那条边出磁场后至另一条边进入磁场前不产生感应电动势，当另一条边进入磁场后，那条边会产生感应电动势。

4    教学启示

电磁感应综合问题一般都会涉及非匀变速运动过程，其中相关物理量的求解需要利用微元思想［２-３］，需加注意。

参考文献：

［１］中华人民共和国教育部． 普通高中物理课程标准（２０１７年版2020年修订）［Ｓ］． 北京：人民教育出版社，２０２０：４－５．

［２］景微安．力学三大观点在电磁感应问题中的应用［Ｊ］． 中学物理教学参考，２０２２，５１（１）：４３－４７．

［３］刘杭州，宋书婷．电磁感应问题中变化的电流问题中电量的计算［Ｊ］．湖南中学物理，２０２１（４）：８９－９１．

（栏目编辑    陈  洁）

收稿日期：2023-03-17

作者简介：赵继辰（1984-），男，实验师，主要从事物理教师教育培训与研究工作。