利用壳层定理求解地球隧道问题

收稿日期：2023-10-13

基金项目：教育部产学合作协同育人项目“物理学前沿问题在《光电子技术》课程教学中的渗透与实践”；重庆市研究生教育教学改革研究项目“理工类学术研究生的多学科交叉融合课程体系探索”（ ｙｊｇ２２３０３５）。

作者简介：崔胜喆（２００３－），男，本科生，主要从事物理学科教学研究。

*通信作者：朱建慧（1987-），女，副教授，主要从事凝聚态物理和物理学科教学研究。

摘   要：地球隧道问题是物理教学、科幻作品和科普教育中常见的物理模型。文章从学生熟悉的高中几何证明思路入手，提出了基于壳层定理的地球隧道问题求解方法。该方法思路简单，理解难度较低，可避免学生在未理解高斯定理内涵的情况下强行利用高斯定理证明地球隧道问题的迷茫。

关键词：地球隧道；壳层定理；高斯定理；类比思想

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2024）3-0073-4

凡尔纳的著名科幻作品《地心游记》设想了一条通过地心、贯穿地球两端的假想隧道。人们可以通过该隧道直通地球两端，并在沿途欣赏地心的奇幻美景。科幻大片《全面回忆》“实现”了凡尔纳的梦想：一条穿越地心的“坠道”直接连通北半球的英国和南半球的澳大利亚，生活在澳洲的人们可乘坐“地铁”穿越地心，经４０分钟抵达英国。而现实生活中，澳大利亚悉尼至英国伦敦的直飞航线全程飞行时间超过二十个小时，相比枯燥又漫长的空中飞行，穿越地心之旅大大缩短了行程时间，也给人类带来了更奇妙的观感和体验。科幻作品中的畅想往往都有现实依据，上述电影中的４０分钟旅程时间是如何确定的呢？该时间和隧道长短有关吗？为解决这些疑问，在此对地球隧道问题展开研究。

地球隧道是物理教学中的常见模型，顾名思义，它是指一条穿行于地球内部的隧道。其几何示意图如图１所示，假设地球是密度均匀的球体，隧道从地球的一端开始，通过地心到达另一端。若只考虑万有引力作用，物体在该地球隧道中做何种运动？物体通过地球隧道的时间又是多少呢？这是一个很有意思的问题。目前，对地球隧道问题的探讨大多都是基于高斯定理的类比推导，从而得出隧道内质点所受万有引力的表达式［１－７］。高斯定理本是电磁学中用来描述静电场内闭合曲面所包围的电荷与电场在闭合曲面上电通量的关系，多用于对静电场分布的描述。因数学上具有相似性，在证明其他平方反比规律的时候也常用到。故多数解法只是简单套用高斯定理，并未详细阐述利用静电场分布规律解释力学过程的原因，导致学生对问题的理解不够深入。因此，为了更加清楚地求解此类问题，本文提出了基于壳层定理的地球隧道问题求解方法，从学生高中时期熟悉的几何证明思路入手，思路简单易懂，理解门槛较低，可避免学生在未理解高斯定理内涵的情况下强行接受。

■

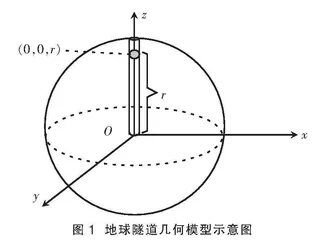
图1  地球隧道几何模型示意图

１    地球隧道问题

为求解地球隧道问题，首先建立地球隧道模型：设地球是半径为Ｒ、质量为Ｍ、密度为ρ的匀质球体，沿其径向过球心挖一条隧道，将位于隧道内的任一物体视作质量为ｍ的质点，ｒ是该质点与地球球心之间的距离（图１）。忽略地球自转的离心惯性力和科里奥利力，在仅考虑万有引力作用的情况下讨论质点的运动情况。

２    高斯定理法

目前普遍利用高斯定理对上述地球隧道问题进行求解，直接套用高斯定理求解出质点与地心之间的万有引力，再根据质点所受引力情况对质点运动情况作出判断，具体求解过程大都很粗略。为了与壳层定理法进行对比，这里再次对基于高斯定理的证明方法进行总结归纳。

如图１所示，以球心为原点，隧道方向为ｚ 轴，建立直角坐标系，则隧道内质量为ｍ的质点位置可表示为 （０，０，ｒ）。根据球对称性，假定质点ｍ所在的球面为一高斯面，此高斯面上的引力场强为ｇ，方向与质点位置矢量ｒ（或面元的法线方向ｎ）相反，即θ角为π，如图２所示。

■

图2  质点m处的高斯面示意图

类比高斯定理，引力场强度对包围该质点曲面的积分为

■g·nds=-4πGρ·■πr3（１）

其中，Ｇ为万有引力常量。又经计算可得

■g·nds=-4πr2g

因此，引力场表达式为

ｇ＝－■πGρｒ（２）

根据牛顿第二定律，得质点在坐标（０，０，ｒ）处的加速度为

■=－■πGρｒ（３）

由（3）式可解得［２］r=Acos（ωt+φ），其中ω=■。故由该结果可知质点运动为简谐振动。根据T=■=■，代入地球的质量密度ρ和万有引力常量Ｇ，即可得简谐振动的周期约为８４分钟。

由此可见，利用高斯定理求解“地球隧道”问题的方法并不复杂。但如果不理解公式（１）的推导和证明过程，就很难理解高斯面与地球表面之间的球壳质量为什么不会对高斯面上的质点产生万有引力。同时，大学一年级的学生尚未完全理解电磁学中高斯定理的物理意义，难以进行高斯定理的类比应用。给学生详细推导和证明高斯公式不失为一种解决办法，但推导涉及的曲面微积分知识过于抽象和复杂，不适用于在大学物理课程教学以及物理科普中详细阐述。基于此，尝试利用更直观、清晰的牛顿壳层定理求解该问题。

３    牛顿壳层定理法

３．１    牛顿壳层定理的推导证明

几何模型与物理问题结合是物理教学经常提及的一种思路，例如，研究带电粒子在磁场中的运动、光的折射与反射等问题时会频繁应用此思路［８－９］。牛顿在《自然哲学的数学原理》中，首次证明壳层定理（ｓｈｅｌｌ ｔｈｅｏｒｅｍ），其也是几何模型与物理问题结合的典型例子。在求解引力场问题时，引入球体几何模型可得具体结论：一个质量为Ｍ、半径为Ｒ的球壳，若其质量呈球对称分布，它在距离球心ｒ处Ｐ点产生的引力场可以做两种等效。当Ｐ点在球壳外（ｒ ≥ Ｒ）时，Ｐ点引力场等效为球心处质量为Ｍ的质点产生的引力场；当Ｐ点在球壳内（ｒ ＜ Ｒ）时，球壳的部分在Ｐ点产生的引力场等于零。

利用解析几何思想证明该结论的具体过程如下：均匀实心球体外存在质点ｍ，其中ｍ到实心球体球心距离为r。为求二者之间的万有引力，可将实心球划为无数个极薄的同心球壳。图３是半径为Ｒ、质量为Ｍ的同心球壳的示意图，质点ｍ与该同心球壳的位置关系如图3所示，其中任一无穷小的圆弧对应的圆心角为ｄθ（图中ｄθ为无穷小角度）。

如图３所示，经过同一球壳上任意一点处的经线所包围的圆环质量为

■

图3   质点在球壳外示意图

dM=■2πR2sinθdθ=■sinθdθ（４）

该圆环dＭ对ｍ的万有引力合力指向球壳中心，表达式为

dFr=■dMcosφ=■■dθ（５）

对（５）式两边不定积分得

Fr=■dFr=■■■dθ（６）

式子中变量为θ，φ，为运算方便下面统一变量为s。由余弦定理得

cosθ=■（７）

故

sinθdθ=■ds（８）

而

scosφ=r-Rcosθ（9）

将（8）（9）式代入（6）式，得质点在球壳外部，即r>R时

Fr=■dFr=■■■（r-■）ds=G■（１０）

推广到质点位于球壳内部时，质点在球壳内示意图如图４，有

Fr=■■[1+■]ds=0（１１）

■

图4  质点在球壳内示意图

故得出，质量分布均匀的球体其内部的万有引力为０。

３．２    利用牛顿壳层定理证明“地球隧道”问题

不妨研究对称的两个质元，如图５所示。质点Ｐ位于球心为Ｏ的均匀球面之内，Ｅ位于球面之上。连接直线ＯＥ，过Ｐ作直线ＡＣ和ＢＤ分别与球面交于Ａ，Ｃ，Ｂ，Ｄ四点，设ＡＣ与ＢＤ的夹角为α，ＡＣ与ＯＥ的夹角为β，并使ＡＣ与ＢＤ的夹角α趋于无限小，则■近似相等于直线ＡＢ，AP≈BP≈r1，DP≈CP≈r2。

■

（a）面积微元

■

（b）球壳整体

图5  面积微元与球壳整体示意图

绕ＯＥ轴旋转，则ＡＢ，ＣＤ形成一个环状球带，设ＡＢ形成球带侧面积为S1，ＣＤ形成球带侧面积为S2，S1与高为ＡＢ（ＡB＝r1sinα）、底面半径为ＡＦ （ＡＦ＝r1sin β）的圆柱侧面积无限接近，易得

S1=2πr■■sin βsinα（１２）

S2=2πr■■sin βsinα（１３）

■=■=■（１４）

■=■·■=1（１５）

由上述结果可以得到，取得的对称两环带S1，S2，对Ｐ点万有引力之和为０。已知球壳可被视为无数对称环带之和，故将结论推广到整个球壳，可得球壳对Ｐ点的万有引力之和为０。这也就解释了为什么高斯定理不考虑高斯面外球壳的引力场。

故可严谨证明，质点所受万有引力为

F■=-G■·M■=-G■·■πr3ρ（１６）

将（１６）式代入牛顿定律，得

F■=m■

得到微分方程

■=-■ρπG·r

由此可见，（１６）式与（３）式结果一样。然后求解二阶齐次微分方程，易解得

r=Acos（ωt+φ）（１７）

由（１７）式，物体在地球隧道内做简谐运动，其中Ａ为振幅，由初始条件可得Ａ等于地球半径Ｒ，ω=■为振动频率。当隧道不经过地球球心，而是地球的一条弦时，可以通过几何关系证明振动的振幅Ａ发生了变化［１，４］，但振动频率和周期并没有发生变化。

４    结  语

牛顿壳层定理为求解地球隧道问题提供了较为新颖的证明方法，弥补了利用高斯定理求解此类问题导致的讨论不深入、学生理解困难等缺陷。同时，相比高斯定理中涉及的曲面积分、求解微分方程等较为复杂的高等数学知识，应用壳层定理解决地球隧道问题的方法则更多借鉴了高中数学中平面解析几何的思想，数学门槛较低，更加普适化且便于理解。同时，可实现“一题多解”，启发学生在面对同一个问题时采用多种方法进行研究，培养其探究精神和创新意识。

参考文献：

［１］吴岱宗，刘玉颖．物体在地球隧道中的运动［Ｊ］．物理与工程，２０２０，３０（１）：７３－7９．

［２］周建丽，陈钢．“均匀球壳对壳内物体引力为０”证明问题的探讨［Ｊ］．物理教师，２０１３，３４（９）：６０－6１．

［３］石凤良，刘一山，邸淑红．穿越贯通南北极隧道的物体与简谐振动［Ｊ］．物理教师（高中版），２００８，２９（２）：２６，28．

［４］覃铭，黄红强．地球隧道运输［Ｊ］．广西物理，２００３，２４（１）：２４－2５．

［５］黄石初．对物体在贯通地球的直隧道内运动问题之商榷［Ｊ］．安徽工学院学报，１９８７（Z１）：１３９－1４８．

［６］杨天才．两平方反比力在球体（壳）模型中的强度公式对比［Ｊ］．数理化解题研究，２０２１（４）：７７－7９．

［７］陈学文，李彦敏．“万有引力场强度”与“万有引力场的高斯定理”［Ｊ］．商丘师范学院学报，２００５，21（５）：１６1－１６3．

［８］唐淑红．高斯定理在万有引力场中的应用［Ｊ］．湘潭师范学院学报（自然科学版），２００８，30（３）：１４－１６．

［９］刘景世．“均匀带电球面上的电场强度如何计算”的再讨论［Ｊ］．河南教育学院学报（自然科学版），２０１１，２０（４）：３２－３３．

［１０］周国全，黄华玲．类比法研究万有引力场的高斯定理［Ｊ］．物理与工程，２０１９，２９（Ｓ１）：２２－２５．

（栏目编辑    蒋小平）