有收尾过程物理现象的类比研究

收稿日期：2023-12-08

作者简介：钟云杰（1987-），男，中学一级教师，主要从事物理教学研究及竞赛教学研究。

摘   要：高中物理涉及到的一些有收尾过程的物理现象，主要涉及动力学和电磁学中的速度、Ｒ－Ｃ及Ｒ－Ｌ振荡电路中的电流、放射性元素的衰变规律等，通过数学推导均能发现自然对数的底ｅ包含其中，且它们的表达式十分相似，推测它们具有某种共性规律。通过先找共性再进行类比分析的思路对此进行了研究。

关键词：收尾过程；类比；微分；竞赛思维

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2024）3-0070-4

自然界中的物理现象有着诸多惊人的相似，说明物理世界有着一种共性美。这种共性可以通过类比得到。虽然高中物理由各板块组成，但是某些物理规律却有着本质的相似。因此，只要把握住关键规律，进行合理的数学推导及演绎，就能获得其共性规律。类比思想对处理这种共性问题有着莫大的作用，本文也将对物理竞赛中学生思维能力的培养提出一些想法。

１    自然界中具有收尾过程的物理现象

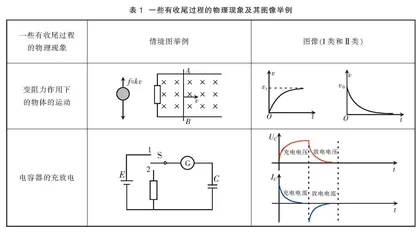
所谓收尾过程，即某物理量变化越来越慢，最终能达到稳定状态。如果绘制出该物理量随时间变化的图像，其斜率会逐渐减小。表1列举了一些高中物理教材中涉及的相关问题。笔者根据这些图像猜测它们应该具有某种共性规律，只要找到这个共性条件，即可根据其中一个的推导思路和结果快速获取其他现象对应的物理规律。研究过程中标记绝对值增加的情况为Ⅰ类，减小的情况为Ⅱ类。

２    物体在有变阻力作用下的运动案例分析

案例 阻力满足ｆ＝ｋｖ的动力学问题

问题Ⅰ（有恒动力系统下的收尾过程） 一个小球从静止开始下落，在下落过程中受到空气阻力，求其速度随时间的变化规律。

由牛顿第二定律，有

mg-kv=m■

整理并两边积分

■■=-■■dt

得

v=■（1-e■）

令最大速度mg=kvm，则有简单形式

v=vm（1-e■）

其中，λ=■。

问题Ⅱ （无动力系统下的收尾过程） 一个小球在光滑水平桌面给其一个初速度v0，运动过程中受到空气阻力，求其速度随时间的变化规律。

由牛顿第二定律

-kv=m■

整理并两边积分

■■=-■■dt

得

v=v0e■

其中，λ=■。

３    类比思想整合某些有收尾过程的物理现象及其规律

从以上动力学条件ｆ＝ｋｖ分析了有动力和无动力的两种运动情境，由此可以推测，只要收尾过程中能满足ｙ＝ｋｘ（ｋ为常量，ｘ为变量）的形式，就有可能得到类似的物理规律。

３．１    从动力学形式类似上进行类比

电磁感应中的动杆问题，除动杆上有电阻Ｒ，其余电阻不计，轨道光滑。

由法拉第电磁感应定律有

ε=BLv

由电路及安培力知识有

FA=■=kv

容易类比得到此安培力的规律类似于动力学问题中的空气阻力，看来两种常规收尾过程（有恒动力或无恒动力）的速度随时间变化规律应类似。可分别得出这两种情况的表达式。

情况Ⅰ 受恒定外力Ｆ作用由静止开始运动。应有

v=vm（1-e■）

其中，λ=■，k=■，F=kvm。

情况Ⅱ 只在安培力作用下以ｖ０开始运动。应有

v=v0e■

其中，λ=■，k=■。

３．２    从微分方程的形式上进行类比

不同于动力学寻找力与速度的关系，电容器中满足的是U=■Q，看情况也能符合ｙ＝ｋｘ的形式。

若电源电动势为Ｅ，限流电阻为Ｒ，其他电阻均不计。充电过程，由闭合电路欧姆定律可得E-■=R■，利用类比思想快速得到此微分方程的最简解。因为这个微分方程与案例中的动力学微分方程在形式上都满足a-bx=c■，因此类比的结果就应是x=■（1-e■），如表２所示。

由此类比法获得的结果与求解微分方程一致，再通过一些数学运算即可获得充电时电流、电压随时间的变化规律。

以此思路亦可快速获得电容器放电时的电量随时间的变化规律

Q=Q0e■

其中，λ=■，Q0为电容器放电时的初始电量。

在自感现象中，若电源电动势为Ｅ，与电感串联的电阻阻值为Ｒ，其余所有电阻均不计，总能找到定值电阻上的欧姆定律U=Ri，符合ｙ＝ｋｘ的形式。所以，通电自感和断电自感中的电流规律也可以利用此类比法。

通电自感的微分方程：E-iR=L■，Ｅ为电源电动势。

断电自感的微分方程：-iR=L■。

通电自感的电流：i=im（1-e■），其中，im=■，

λ=■。

断电自感的电流：i=i0e■，其中，i0=■，λ=■。

对于放射性元素的衰变规律应满足■=

-λm，反映的是因衰变质量的减少率与当前质量成正比，由于绝对值在减小，故属于Ⅱ类问题。由以上经验可快速得到其最简解m=m0e■，ｍ０为衰变计时起点时的质量。

３．３    利用初末状态处理极值和单位制解决λ系数

由以上讨论可以发现，最终稳定状态的方程均是ｙ＝ｋｘ形式，研究微分变量ｘ的稳定状态是很容易分析出来的，比如变力作用下的动力学问题。对Ⅰ类问题可知末状态是稳定态，可以直接分析此状态下的稳定方程，即mg=kvm，以此得到稳定时的最大速度解。

再来看系数λ。由之前的规律可知，结果均是ｅ的时间指数解e■，但是指数上必须是常数，不然无法求出ｅ的幂，因此根据单位制很容易发现λ的单位是ｓ－１。由条件可知，ｋ的单位为ｋｇ/ｓ，故猜测λ系数的表达形式为λ=■。

有了以上经验，可以对其他收尾过程进行验证，如表３所示。

以上结果经检验均正确，Ⅱ类问题的分析读者也可自己进行。

４    结  语

很多物理问题都可以通过数学来进行描述，常用方法就是利用微分方程求解。在培养学生竞赛思维上，如果能对各种物理问题进行总结归类，那么无疑可以减少记忆量、运算量，还能将一些不同模块的问题统一化，可以是情境条件的统一，也可以是求解方法的统一，亦可以是分析方法的统一。本文主要就某类物理（下转第76页）（上接第72页）现象——有满足ｙ＝ｋｘ形式的收尾过程，表达了类比思想的重要性。总而言之，教师在培养学生竞赛思维上有很多途径，而利用已有模型类比解决未知问题是竞赛中常用的方法，建议竞赛中可以强化这个意识。

参考文献：

［１］温斯琼，潘苏东．物理教科书中类比策略的分析——以新人教版高中物理教科书为例［Ｊ］．中学物理，２０２１，39（9）：25-29.

［２］张立新．从物理学中数学常数ｅ思考数学之自然属性［Ｊ］．首都师范大学学报（自然科学版），２０１５，36（3）：25-29.

（栏目编辑    蒋小平）