对一道物理选择题“一题多解”的深度剖析
作者: 刘荣
收稿日期:2023-11-22
作者简介:刘荣(1984-),男,中学一级教师,主要从事高中物理教学研究。
摘 要:通过对一道物理选择题“一题多解”出现不同结果的教学案例进行分析,发现学生学习过程中存在的问题,引导学生回归教材,温故知新。
关键词:运动的合成;运动的分解;相对性原理
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2024)4-0074-3
1 提出问题
运动的合成与分解是处理曲线运动的一种常用方法,它可以化曲为直,将复杂、陌生的运动分解成简单、熟悉的运动进行研究,使问题的解决得以简化。但学生在解决该类问题时往往凭借已有的学习经验生搬硬套。笔者在教学过程中就遇到了一道典型的问题,原题如下:
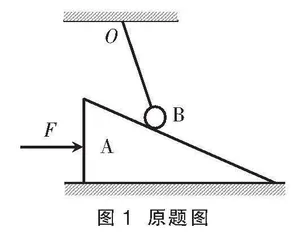
如图1所示,一根细绳的上端系在O点,下端系一个重球B,放在粗糙的斜面体A上,现用水平推力F向右推斜面体使之在光滑水平面上以某速度向右匀速运动一段距离(细绳尚未到达平行于斜面的位置)。在此过程中( )
A.重球B做匀速圆周运动
B.摩擦力对重球B做正功
C.水平推力F和重球B对斜面体A做功的绝对值大小相等
D.斜面体A对重球B所做的功与重球B对斜面体A所做的功绝对值大小相等
■
图1 原题图
解析 重球B的受力分析、运动轨迹如图2所示。摩擦力与位移的夹角为锐角,故摩擦力对重球B做正功,B选项正确;斜面体A匀速运动其动能不变,合外力做功为0,故C选项正确;A对B的作用力与B对A的作用力大小相等,但由于A和 B之间有相对滑动,故其位移大小不等,D选项错误。下面重点分析A选项。
■
图2 受力分析
解法一 如图3所示,将重球B的速度vB分解为水平方向的速度v和沿绳方向的速度v1。由几何关系可得vB=vcosθ,重球B运动过程中,绳与竖直方向的夹角θ逐渐增大,故vB逐渐减小。
■
图3 速度分析一
解法二 如图4所示,将重球B的速度vB分解为水平方向的速度v和竖直方向的速度v2。由几何关系可得vB=■,重球B运动过程中,绳与竖直方向的夹角θ逐渐增大,故vB逐渐增大。
■
图4 速度分析二
解法三 如图5所示,将重球B的速度vB分解为水平方向的速度v和沿斜面方向的速度v3。重球B运动过程中,绳与竖直方向的夹角θ逐渐增大,则vB与水平方向的夹角逐渐增大,但水平分速度v恒定,沿斜面方向的分速度v3方向不变。由图6可得,vB先减小后增大。但由于题目要求细绳尚未到达平行于斜面的位置,当绳与斜面平行时,vB恰好与v3垂直,故该过程中vB逐渐减小。
■
图5 速度分析三
■
图6 速度分析四
2 解法剖析
三种解题方法的焦点是重球B在水平方向的分速度与斜面体的运动速度是否相等。如图7所示,解法一将重球的运动等效为先沿水平方向运动,再沿绳子方向运动。解法二将重球的运动等效为先沿水平方向运动,再沿竖直方向运动。这两种解法重球的水平分位移明显小于斜面体的位移,故其水平分速度小于v。解法三将重球的运动等效为先沿水平方向运动,再沿斜面方向运动,其水平分位移恰好等于斜面体的位移,即重球水平分速度等于斜面体的速度v,解法三正确,重球B做速度减小的圆周运动,A选项错误。解法一和解法三的结果虽然相同,但解法一仅仅是重球B运动过程中末状态(绳子与斜面平行)的情况(只有末状态时水平速度等于v),用一个特殊的状态描述一个一般的过程,显然是不妥的。
■
(a)解法一
■
(b)解法二
■
(c)解法三
图7 三种解法对比
3 错解归因
笔者查阅了几本教辅用书,该题的解法都采用解法一,基础较好的学生对解法一也比较认可,究其原因是受到收绳问题的影响(如下题)。
如图8所示,人在岸上捉住绳上的A点以速度v0水平向左匀速拉动轻绳,绳跨过定滑轮拉着在水面上向左移动的小船B。若某一瞬间绳与水平方向的夹角为θ,则此时小船B的速度v为多大?
■
图8 人拉船问题
解析 如图9所示,小船的运动可等效为绕定滑轮的转动和沿绳子方向的上升,由几何关系可得小船的速度v=■。
■
图9 对人拉船的运动分析
收绳问题之所以这样分解,关键在于绳子是不可伸长的,定滑轮左侧绳子的伸长量和定滑轮右侧绳子的缩小量相等,从而决定了小船沿绳子上升的速度与拉绳的速度相等。
受平抛运动研究方法的影响,大多数学生比较认可解法二。平抛运动是高中学生第一次接触到利用合成与分解的思想研究曲线运动,同时也使学生意识到可以通过分解的方法将一个陌生的运动分成两个熟悉的运动(匀速直线运动和自由落体运动),给学生留下了深刻的印象。也正是这种成功的学习经验的应用催生了解法二,但学生并没有意识到将重球B的运动分解成水平和竖直两个方向的分运动是否为他们所熟悉的,这两个分运动是否可解。
4 思维提升
运动的合成与分解是描述运动的位移、速度、加速度的合成与分解,其方法是平行四边形定则。一个矢量根据平行四边形定则可以分解在任意两个方向上,可以有无数对的分量。按照这一原则,三种分解方法都是可行的,但根据伽利略相对性原理的速度变化关系:“绝对”速度等于牵连速度与相对速度的矢量和[1],则重球B相对地面的速度等于斜面体相对地面的速度与重球B相对斜面体的速度的矢量和,显然只有解法三正确。
学生之所以出现上述问题,从表面上看是对“成功学习经验”的应用,其实质是对相对性原理的理解不透彻,应用不灵活。为了消除学生在解答该类问题时的思维困惑,笔者在上述教学后又以粤教版必修2第一章章末习题第1题为例引导学生分析。原题如下:
雨点以3 m/s的速度竖直下落,行人感到雨点与竖直方向成30°角迎面打来,那么人行走的速度是多少?
解析 不妨设人向右行走,其速度大小为v,雨滴相对人的速度为v1,雨滴相对地面的速度为v2。
解法一 以人为参考系,根据速度变化关系,雨滴相对人的速度等于地面相对人的速度与雨滴相对地面的速度的矢量和(图10),由几何关系得人行走的速度v=v2tan30°=1.73 m/s。
■
图10 以人为参考系
解法二 以地面为参考系,根据速度变化关系,雨滴相对地面的速度等于人相对地面的速度与雨滴相对人的速度的矢量和(图11),由几何关系得人行走的速度v=v2tan30°=1.73 m/s。
■
图11 以地面为参考系
两种解题方法虽选择不同的参考系进行解答,但最终“殊途同归”。通过该题的分析加深学生对相对性原理的理解,同时使学生体会到运动是相对的,对物体运动的描述都是相对于某一参考系。根据相对性原理,在研究力学现象时,一切惯性参考系都是等价的。
参考文献:
[1]周衍柏.理论力学教程(第2版)[M].北京:高等教育出版社,1986:21.
(栏目编辑 蒋小平)