浅谈带电粒子在“运动磁场”中的受力及运动问题

摘   要：基于对带电粒子在“运动磁场”中做摆线运动的讨论，利用洛伦兹变换确定不同惯性参考系下电磁场的分布，指出在实验室参考系中，运动磁源会在空间产生磁场和感生电场，感生电场力对带电粒子做功，洛伦兹力表达式中的速度v是相对于观察者的，永不做功；迁移分析相关的高考和模拟题，指出传统的求解对学生物理观念的形成存在误导，以此浅谈对此类问题的教学与命题建议。

关键词：运动磁源；洛伦兹变换；感生电场；洛伦兹力

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2024）8-0068-4

１９０５年，爱因斯坦在创立狭义相对论时曾举例，磁铁与线圈发生相对运动时，以磁铁为参考系产生动生电动势，以线圈为参考系则产生感生电动势，同一物理现象在不同参考系下描述结果不同，根本原因在于电磁场的分布与参考系的选取是有关的。

中学生对运动电荷在静止匀强磁场中的运动规律非常熟悉。但在高三复习备考乃至高考中，常常会出现“运动磁场”对静止电荷作用使其运动等相关问题，学生常常会感到困惑，到底是什么力对电荷做功使其具有动能，洛伦兹力公式中的速度ｖ究竟是相对磁场还是相对观察者的？基于对一道典型试题的分析，利用洛伦兹变换确定不同惯性参考系下电磁场的分布，指出在实验室参考系中，运动磁源在空间中会产生磁场和感生电场，在感生电场力和洛伦兹力的共同作用下带电粒子做摆线运动。迁移分析其他典型试题，指出传统的处理结果虽然正确，但对学生物理观念的形成存在误导，以此浅谈对此类问题的教学和命题建议。

１    提出问题

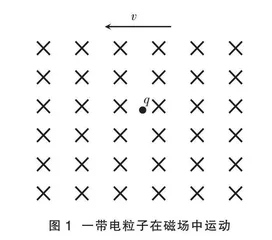
例１  如图１所示，假定空间中存在垂直纸面向里的匀强磁场Ｂ，并以速度ｖ向左匀速运动，在其中放置一个电荷量为ｑ、质量为ｍ的带正电的初速度为０的微观粒子，不计带电粒子的重力，试分析带电粒子在该磁场中的运动。

分析与解答 此题为带电粒子垂直进入静止匀强磁场的逆过程，即相对于地面，初始情况下粒子静止而磁场运动。通常处理这类问题的思路是利用伽利略相对性原理，将带电粒子相对地面的运动视为其相对磁场运动与磁场相对地面运动的矢量和。

以磁场Ｂ为参考系，带电粒子以速度ｖ向右垂直进入磁场。此时，带电粒子在洛伦兹力的作用下，相对磁场做逆时针方向的匀速圆周运动。不难得出，带电粒子相对地面的运动为匀速圆周运动与匀速直线运动合成后的摆线运动［１］，其运动轨迹如图２所示。

提出问题 中学生对上述解答过程是不难接受的，但大多数学生常常会有疑惑：相对于地面，带电粒子初速度为０，运动磁场与之作用过程中，是什么力对带电粒子做功使其具有动能，洛伦兹力究竟做不做功？通常情况下，教师会引导学生从能量守恒的角度思考问题，即维持磁场匀速运动的外力是需要对此系统做功，是外力做功转化为带电粒子的动能。此番引导很难消除学生对洛伦兹力永不做功的质疑，即外力做功是怎么转化为带电粒子的动能呢？有必要对此问题进一步研究。

２    追根溯源

２．１    场的特性

物理学早已证实，场是一种客观存在的物质，反映空间某点的情况，它是把物理状态作为空间和时间的函数来描述。若物理状态与时间无关，则为静态场；反之，则为动态场或时变场。没有运动的场，只有运动的场源，磁体的运动只会带来空间各处变化的磁场和涡旋电场，而不会带来运动的场［2］。因此，题干中关于运动磁场的表述是不妥的，确切表述应该是带电粒子在运动磁源产生的电磁场空间内的运动。为便于讨论，在此仍沿用习惯上“运动磁场”的表述。

２．２    不同参考系下电磁场的分布

相对论指出，将电磁场分为电场部分和磁场部分只有相对的意义，电磁场作为一个整体，在不同惯性参考系下满足同样的规律，不同惯性参考系下的电磁场分布可用洛伦兹变换找到联系。下面分别表达相对于地面静止的∑系与相对于运动磁源静止的∑'系，三维空间中的电场Ｅ和磁场Ｂ的分布，如图３所示。在∑'系中

２．３    感生电场力做功，洛伦兹力永不做功

由以上讨论，相对磁源（∑'系），只存在B'z=

-B，带电粒子只受到洛伦兹力，做匀速圆周运动，此时洛伦兹力不做功；相对地面（∑系），同时存在Bz=-B和Ey=vB，带电粒子将受到感生电场力，即F=qEy=qvB，大小恒定，方向向上，F对带电粒子做功使其获得速度，洛伦兹力只是改变其速度方向，并不做功，在F和f的共同作用下，带电粒子做摆线运动。

由此，f表达式中的速度始终是相对于观察者的，永不做功；在实验室参考系，运动磁源产生了感生电场，是感生电场力对带电粒子做功使其具有动能。中学阶段受数学等因素所限，常常转变参考系，对感生电场避而不谈［3］。但在高考和各地模拟试题中出现类似试题时，其求解过程常常对学生造成误导，下面各列举一道高考题和模拟题进行点评分析。

３    相关高考和模拟试题

例２  如图４所示，将一质量为ｍ、电荷量为ｑ的带正电小球轻放在光滑绝缘地面上，使其处于“Ｕ”形磁铁间的磁场中，磁场视为匀强磁场，大小为Ｂ，方向垂直纸面向外。试问为使带电小球恰好可以离开地面，应怎样移动磁铁（     ）

点评  此题出自于某地的模拟卷，考查学生对左手定则的掌握以及简单的受力分析能力，参考答案是Ｄ。根据二力平衡，qvB=mg，化简得v=，再借助左手定则易得答案为Ｄ。解答过程对学生来说不难，但大部分学生可能会想当然地认为这里的qvB是洛伦兹力，表达式中的ｖ是小球相对磁场的速度。实际上，这种想法是不妥的。真实情况是由于磁体相对地面向右运动，产生了向上的感生电场E=vB，小球受到的力是感生电场力，即F=qE=qvB。因此，这里很容易误导学生，使其认为洛伦兹力qvB中的速度是相对磁场的。

例３   如图５所示，两条相距为ｄ的平行金属导轨位于同一水平面内，其右端接一阻值为Ｒ的电阻。质量为ｍ的金属杆静止在导轨上，其左侧的矩形匀强磁场区域ＭＮＰＱ的磁感应强度大小为Ｂ，方向竖直向下，当该磁场区域以速度v0匀速地向右扫过金属杆后，金属杆的速度变为ｖ。导轨和金属杆的电阻不计，导轨光滑且足够长，杆在运动过程中始终与导轨垂直且两端与导轨保持良好接触。求：

（１）ＭＮ刚扫到金属杆时，杆中感应电流的大小Ｉ；

（２）ＭＮ刚扫到金属杆时，杆的加速度大小ａ；

（３）ＰＱ刚要离开金属杆时，感应电流的功率Ｐ。

点评  此题为２０１７年江苏省高考计算题第１题，考查学生对简单电路计算及基本动力学问题的分析能力。试题第（１）（２）问，学生易得感应电动势E=Bdv0；试题第（３）问，学生也不难得到ＰＱ刚要离开金属杆时的感应电动势为E=Bd（v0-v）；然后，分别结合闭合电路欧姆定律、牛顿第二定律以及焦耳定律完成作答。

大多数学生在处理此题时都会将这里的感应电动势理解为动生电动势，即由于导体棒切割磁感线而产生的，由此错误地认为课本上讲的动生电动势E=Blv中的速度为导体棒相对磁场的速度。实际上，动生电动势表达式中的速度ｖ是相对观察者的，因为其非静电力与洛伦兹力有关，而f=qvB中的速度ｖ是相对观察者的。在默认地面为参考系的情况下，本题第（１）问应是运动磁场产生感生电场E=v0B，从而使金属杆产生感生电动势E=Bdv0；而第（３）问的电动势，应为运动磁源产生的感生电动势与导体棒运动产生的动生电动势的代数和，即E=E-E=Bdv0-Bdv。虽然结果都一致，但不得不说此类试题在一定程度上潜移默化地使学生对物理概念产生错误的理解。

４    教学与命题建议

中学教材中磁源相对实验室参考系一般都是静止的，这就避免了对感生电场的讨论。相对实验室参考系，一旦磁源运动起来，将产生感生电场，空间同时存在着电场和磁场。分析此类问题时，以磁场为参考系虽然可以避免感生电场的讨论，但常常会促使学生错误地认为洛伦兹力公式中的速度ｖ是相对于磁场的。在一定条件下，洛伦兹力是可以做功的，也会误导学生认为电磁感应中的动生电动势表达式中的速度也是相对磁场的，不利于学生养成科学的物理观念。因此，面对普通学生，有关场源运动类的试题应该尽量避免出现。（下转第73页）

（上接第70页）

需要指出的是，高等物理《电动力学》将电磁力=q（+×）统称为洛伦兹力［4］，这是洛伦兹力广义上的定义。从这个意义上说，当电磁力对电荷做功时，也确实可以说是洛伦兹力能做功。中学阶段只将运动电荷在静止磁场中的受力定义为洛伦兹力，这是面对初学者受制于数学等因素而采取的对洛伦兹力狭义上的定义，按照这个定义洛伦兹力永不做功。因此，对于数学功底扎实的部分优秀中学生，在竞赛和培优等教学过程中，渗透此类问题并展开分析讨论，是利于学生形成清晰准确的物理观念，可助力对拔尖创新人才的培养［2，５］。

参考文献：

［１］范雄兵．“配速法”巧解复杂曲线运动问题——２０２３年江苏省高考物理最后一题的两种求解［Ｊ］．中学物理，２０２３，41（17）：５４－５５．

［2］李勇．巧借一道“错题”促进学生深度学习［Ｊ］．物理教学，２０２２，44（５）：５８－６０，64．

［3］阮传志．ｑｖＢ是什么性质的力［Ｊ］．中学物理教学参考，２０２３，５２（22）：１１－１２．

［4］罗琬华．电动力学［Ｍ］．重庆：西南师范大学出版社，２０１０．

［５］李勇．用能量观点巧解一道高中物理竞赛题［Ｊ］．物理教学探讨，２０１８，３６（１１）：４３－４５．

（栏目编辑    蒋小平）