弹性碰撞与圆周率的奇妙联系

摘   要：数学中的圆周率与物理中的弹性碰撞看似毫无瓜葛，通过数学变换和几何图像法揭示了圆周率与弹性碰撞的奇妙联系。

关键词：数学几何图像;弹性碰撞次数;圆周率

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2022）7-0059-3

中国古人计算圆周率是采取“割圆术”，南北朝时期的祖冲之在此基础上将圆周率精确到小数点后的第七位，远领先于同时期的国外圆周率的研究[1]。而谈到圆周率，我们往往想到的是数学中的求圆面积公式;谈到碰撞，则往往想到的是物理中的弹性碰撞和非弹性碰撞。那么，弹性碰撞和圆周率有什么联系呢？下面对此进行研究。

1    弹性碰撞分析

此问题并不复杂，我们首先从高中物理中一个常见的碰撞概念说起。两个物体之间在极短时间内产生很大的相互作用力，然后速度发生了变化，这个过程就是碰撞。碰撞又可分为弹性碰撞（无机械能损失）、非弹性碰撞（部分机械能损失）和完全非弹性碰撞（机械能损失最大），本文所研究的是弹性碰撞范畴。

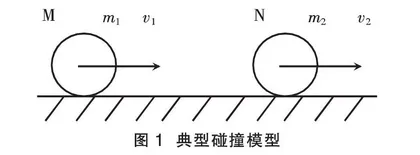
弹性碰撞中，最典型的一个碰撞模型如图1所示。

在水平地面上有两个小球，球M的质量为m1，以速度v1水平向右运动，另一个球N的质量为m2，以速度v2也水平向右运动，且v1>v2，两速度在同一直线上，问两球碰撞之后的运动状态如何？

通常求解该问题时，我们都要利用动量守恒定律和机械能守恒定律得到两个等式，然后再利用代数的方法进行求解，其中这两个等式为

m1v1+m2v2=p（1）

但除了常规的代数求解外，我们还可以利用数学中的几何方法进行求解。那么，要怎样利用几何法进行处理呢？这里，只要将v1和v2分别作为横坐标和纵坐标建立在一个平面坐标系中即可。仔细观察（1）式可以发现，将其画在平面坐标系中就是一条直线。但是（2）式的画法就比较麻烦，仔细观察，其方程式画出后将是椭圆的图像，这不利于分析。为了更加简便，需要将其改造成圆的方程式。令xv2，即（1）和（2）式变换为下式所示：

x2+y2=2Ek（4）

通过变换，我们成功地将方程简化，由此便很容易将动量和能量所对应的图像联立画出，如图2所示。

其中，圆所对应的半径大小为，也就是Ek保持不变。其中的直线就是碰撞过程中动量守恒的方程。而在碰撞过程中需要同时满足动量守恒和能量守恒，则只可能是两个图像相交的A、B两点。也就是说，一开始两物体若是A点状态，则碰撞后必将是B点状态，反之亦然。从图像中还可以得到直线的斜率 以上推论说明，通过数学中几何的方法可以有效解决物体的碰撞问题。

2    圆周率与碰撞的联系

那么，圆周率是怎么跟碰撞产生联系的呢？假设有弹性非常好且光滑的竖直固定墙和水平地面，地面上左边放着物体M，其质量为m1（质量小）;右边放着物体N，其质量为m2（质量大）。如图3所示，初始物体N以初速度v0向左运动与物体M发生碰撞，随后物体M将会向左撞向墙面并反弹再撞物体N，如此反复碰撞直至停止，如果我们去统计物体M的碰撞次数，会发现碰撞的次数和圆周率的大小有着紧密联系。分析可知，由于该过程还是弹性碰撞，所以依旧可以采用上文求得的几何关系来进行深入分析。

为了保持与前文一致，在这里规定水平向右为正方向，则此时最初的状态，x0=1=0，y0=v2=0。据此画出初始时刻的动量几何图像，再根据上文推导的能量方程画出其能量几何图像，此时动量图像与能量图像相交于O和A两点，A点状态即为第一次碰撞后的结果。此时x和y皆为负值，即m1和m2都会向左运动。随后，m1将会与墙面碰撞，其速度将会等大反向，即x值变为相反数;m2的速度则保持不变，即y不变。此过程，m1的速度变化在图像中则表示为关于y轴对称的一条直线，其与圆的交点记为B。随后m1和m2又将相互碰撞，在图中继续画出一条斜线，与圆交于点C。同理，继续与墙面碰撞后可画出点D。最后一次碰撞将会处于点E，如图4所示（此图仅为相互碰撞的一种情况的图像）。此时m1将无法再与墙面碰撞，并可进行碰撞次数统计。显然，碰撞的次数和直线的倾斜角θ紧密联系，倾斜角越小，碰撞次数越多，其中tanθ=。

继续根据图像可以分析得到，每碰撞一次对应着一段圆弧，而这段圆弧所对应的圆周角是θ，则可以得到碰撞N次之后，总的角度之和会比圆的圆周角小，即比圆周率的值略小，而碰撞N+1次后，会与圆周率的值相等或略大于圆周率，即

Nθ<π≤（N+1）θ（5）

进一步化简可得

据此，可根据和碰撞次数N列出如表1中所示的数据。其中，当tanθ=趋近于无穷小时，根据极限可知θ=，即N=π。因而若越小，则得到的碰撞次数就更加接近于圆周率的倍数，进而得到碰撞与圆周率的奇妙关系。

3    总  结

本文通过非常规的数学几何图像的方式，推导得到圆周率与物体弹性碰撞之间奇妙的定量关系，揭示了数学与物理之间的奇妙联系，同时也说明了具备良好的数学素养则可以更好地体会物理之美。

参考文献：

[1]孙宏安.祖冲之与圆周率计算[J].数学通报，1996（8）： 45-46.

（栏目编辑    蒋小平）