初中数学学生思辨力提升策略研究

思辨是一种高阶思维，有思考、辨析之意，释为运用逻辑的推导进行理论思考。思辨的数学课堂，不仅强调让学生关注数学知识本身，培养学生的数学思维，更侧重让学生学会运用数学的思维方式解决现实问题。在新课标的指引下，教师应对课堂教学进行新的设计，构建能够发展学生思维品质的理想课堂；与学生建立融洽的交流氛围，通过引导、提问等方式，激发学生思维的火花。

一、引入生活情境，创造思辨契机

课堂中，教师可以通过引入生活情境来创造引发学生思辨的契机，引导学生把现实问题转化为数学问题，让学生学会构建数学模型，运用数学思维解决现实问题。在构建数学模型的过程中，学生能够发现问题，设计解决方案，并能运用所学知识解决问题，提升对知识运用的能力。

例如，在教授苏科版数学七（下）“用二元一次方程组解决问题”这一课时，笔者创设生活化情境引入课题，引导学生思辨。笔者给每名学生一根长为40cm的彩带，让学生用双面胶将彩带两端粘在一起然后用双手撑出一个长方形。由于学生两指间的长度不同，因此，学生用长度相等的彩带撑出了长宽不同的长方形。此时，笔者再加以引导。

师：我们可以确定长方形的长和宽吗？

生1：设长方形的长为x，宽为y，可以得到方程x+y=20，但是，没有办法确定长方形的长和宽。

师：为什么？

生2：条件不够！一个方程里有两个未知数。

师：那么，有谁可以通过添加合适的条件来解决这个问题吗？

（小组合作交流，尝试通过添加相关的条件，进而确定长方形的长和宽。）

小组1：我们小组添加了条件“长是宽的3倍”，可以得到方程x=3y，再根据方程x+y=20，就能算出长方形的长和宽。

小组2：我们小组本来想添加条件“长比宽多4倍”，但是算出来结果不是整式，于是换了“长比宽多3倍”，这样可以得到方程x=4y，并且算出来的结果是整数。

师：真不错，不仅考虑了条件，连结果都设计得很简洁。

小组3：我们小组设置了比例，长比宽等于5[∶]3。

师：很好，考虑到了比例关系，这也是数学计算中经常用的方法。

【设计意图】笔者根据生活实际，让学生动手操作，让他们直观感受生活中的数学问题。以确定长方形的长和宽为触发点，引导学生思辨，让学生主动构建数学模型，并利用所学解决现实问题。在“发现问题→引发思辨→构建模型→解决问题”的过程中，学生的思辨能力得到了提升。

二、引发认知冲突，激发思辨动力

学生在遇到问题时，会根据已有的生活或学习经验进行判断，结果往往与事实有所偏差。教师可以加以利用，主动引发学生的认知冲突，加深学生对知识的理解，让学生在认知的冲突中激发思辨的动力。

例如，学生在学习苏科版数学七（下）“幂的运算”这一节课之前，已经学习了有理数的加法与减法、有理数的乘法与除法、有理数的乘方、整式的加法与减法等运算。类比前面的学习规律，笔者先从幂的加法开始。

师：如何计算am+bn？

生1：ambn。

生2：abm+n。

……

师：怎么验证你的结论？给a赋值3，b赋值4，得31+42=3+16=19；31×42=48；3×41+4=3072……

师：为什么所得结果是不同的？

（学生开始产生认知冲突，思考到底怎么算。）

师追问：（1）如何计算am+an？（底数相同，指数不同）

（2）如何计算am+bm？（底数不同，指数相同）

（3）如何计算am+am？（底数相同，指数相同）

经过讨论，学生发现：当幂的底数和指数都是数字时，可以进行加法运算，但要先求出各项；如果在幂的底数和指数中含有未知数，那么只有当底数和指数都相同的情况下，才可以进行加法运算，对应的其实是整式的加法中合并同类项的运算法则。

【设计意图】通过举例说明、推理验证等方式制造矛盾点，引发学生思辨，从而归纳出幂的运算法则。在这个过程中，学生经历了“类比→验证→思辨→总结”的思维过程，逐步厘清了各个分化知识脉络之间的区别，构建了完备的知识体系。

三、设计开放性问题，拓宽思辨广度

学生在探究开放性问题时，会从多角度、多方面提炼信息，对问题进行深度挖掘，他们思维的深度和广度可以得到提升。因此，教师在课堂教学中可以设置开放性问题，促使学生思辨，引导学生讨论，拓宽学生的思辨广度。

例如，笔者在教授苏科版数学七（上）“线段、射线、直线”这一节课时，在教授完线段、射线、直线的基本定义、表示、读法、性质等知识点后，设计了开放性问题让学生思考、讨论。

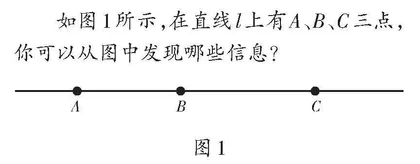
如图1所示，在直线l上有A、B、C三点，你可以从图中发现哪些信息？

生1：我找到一些线段，比如，线段AB、线段BC和线段AC。

生2：我找到了一些射线，有射线AB、射线BA、射线BC和射线CB。

生3：我找到了一条直线AC。

生4：线段AC的长度等于线段AB和线段BC的长度之和。

师：你的发现很有价值，揭示了线段与线段之间的数量关系。

生5：我发现线段BC的长度大于线段AB长度；线段AC的长度大于线段BC和线段AC的长度。

师追问：同学们都找得很好。那么，如图2所示，如果在把点B移到直线外，刚刚你们发现的结论还成立吗？

（让学生作直线AB和BC，如图3所示，并让学生对此图展开讨论。）

【设计意图】通过探究开放性问题，学生对线段、射线、直线进行归类、辨识和再发现，进一步感受图形与图形之间位置关系的变化而引起的数量关系的变化，在思辨中巩固对图形相关性质的理解，逐步完成对知识体系的构建。如果说学生在探究中发现了线段与线段之间存在着一定的数量关系是他们成长的契机，那么笔者设计的追问环节就是引发学生思辨的触发点，在改变图形的位置后，引导学生思考相对应的变化。

四、开展项目式学习，强化思辨能力

项目式学习不仅可以让学生巩固课堂知识，还能提供更多师生和生生之间互相学习和交流的机会，让学生进入深度探究的实践活动中，强化学生思辨能力。

例如，学生在学习了苏科版数学八（上）第三章“勾股定理”后，对勾股定理的历史背景和应用产生了兴趣。笔者和学生一起制定了“漫话勾股”项目式学习活动的方案，从历史发展、社会生活、人文艺术、科技应用等方面提出四个子项目，引导学生选择感兴趣的项目进行学习，将“发现→思辨→应用”延伸到课堂之外。在活动中，学生不仅了解了勾股定理的发现历史，而且还尝试运用不同的方法证明勾股定理，并利用现有的材料，完成“勾股树（图4）”和“立交大桥（图5）”等手工作品。

【设计意图】从了解知识的发展历史开始，到尝试独立证明知识，再到合理运用知识，学生感受到知识是用来解决现实问题的，能够提升对知识的应用能力。

思辨的课堂强调让学生深度思考、判断性分析和创新性解决问题。在这样的课堂上，教师应合理引入教学情境，创新教学模式，通过开展项目化学习等方式来激发学生的思辨动力，提高学生的认知水平，进而发展数学核心素养。<F：＼制作文件备份＼2024年＼初中生-教研＼初中生教科研2024第5期＼Image＼尾标.tif>

（作者单位：江苏省苏州外国语学校）