在探究中感悟本质，在思考中发展思维

2023年江苏省泰州市学业水平考试数学试卷第16题（以下简称“第16题”）是一道图形旋转与翻折的填空压轴题，在考查相关数学知识的同时，重点考查学生的几何动态探究能力、数学本质感悟能力、有序思考与反思质疑能力。本文基于“第16题”的思路分析与问题剖析，谈谈“在探究中感悟本质，在思考中发展思维”的数学教学策略。

一、试题呈现

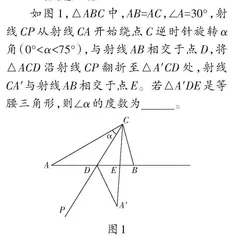
如图1，△ABC中，AB=AC，∠A=30°，射线CP从射线CA开始绕点C逆时针旋转α角（0°<α<75°），与射线AB相交于点D，将△ACD沿射线CP翻折至△A′CD处，射线CA′与射线AB相交于点E。若△A′DE是等腰三角形，则∠α的度数为           。

二、问题剖析

本题以填空题形式出现，不需要书写过程，答案错误或部分正确均不给分。据了解，该题正确率不到1%，完全出乎预料，绝大多数学生少了答案∠α＝67.5°。尽管试题具有一定的难度，但探究方法、分析思路比较常规，没有标新立异。那么，为什么得分率如此之低呢？笔者认为主要有以下几个原因：信息提取不完整，理解不准确；图形特征被忽视，未抓住本质；数学思维套路化，缺乏有序性；探究路径不清晰，策略不明确等。从学生答题情况来看，不少学生对动态问题的研究路径不清晰，不知道从什么地方入手、如何入手，缺乏探究动态问题的合理策略与有效方法。

三、应对策略

1.发挥教材作用，引导学生追根溯源

教材是学生学习的载体，也是数学命题的源头。本题所运用的等腰三角形分类、图形的翻折变换都能从教材中找到源头，例如苏科版数学八年级上册“2.5  等腰三角形的轴对称性”习题第1题：（1）已知等腰三角形的周长为10，底边长为4，求它的腰长；（2）已知等腰三角形的周长为10，腰长为4，求它的底边长。第6题：在△ABC中，∠A=60°，当∠B为多少度时，△ABC是等腰三角形？这两道习题正是以等腰三角形的研究为载体渗透分类的思想方法。另外，这一章还专门安排了“折纸与证明”的数学活动，旨在让学生通过操作探究活动进一步感受图形翻折的数学本质。因此，教师在教学过程中要充分发挥教材的作用，一方面，在研究数学问题（包括中考题）时，要引导学生追根溯源，从教材中找到原型、方法和依据，感受数学问题的来路；另一方面，要利用教材例题、习题、数学活动、数学阅读等素材，引导学生通过探究与思考，提炼数学的本质与方法，并将教材问题拓展与延伸，寻找教材问题的去路。

2.加强数学阅读，准确提取信息

数学和其他学科一样也需要阅读，在阅读中提取信息，在阅读中理解思考，在阅读中批判质疑。比如，本题比较容易得到∠α为22.5°和45°，此时要思考：试题中为什么有0°<α<75°的条件？有没有必要对45°<α<75°的图形进行研究？另外，题目提供的图形中，点A′在射线AB的下方，然而在该动态问题中，随着射线CP绕点C旋转，点A′一直在射线AB的下方吗？通过图文信息的阅读与思考，试题中所隐藏的信息很快便浮出水面。

3.关注探究过程，积累活动经验

《义务教育数学课程标准（2022年版）》提出了积累数学基本活动经验的教学要求，并将“基础知识和基本技能”“数学的思想与方法”“数学核心素养”明确为数学教学目标的重要组成部分。数学教学要关注探究过程，引导学生经历观察、操作、猜想、推理、验证等数学活动过程，积累数学活动经验。例如，本题中的条件“△A′DE是等腰三角形”，此时应要思考哪两条边相等，需要分类讨论，这是基于对开放性问题的探究经验；条件中的“射线CP从射线CA开始绕点C逆时针旋转α角（0°<α<75°）”，表明这是一个连续的运动过程，需要依次画出各种状态（包括临界状态）的图形，思考点A′的位置与△A′DE的形状，并尝试探究使△A′DE为等腰三角形时角与角之间的数量关系，这需要有对动态问题的操作探究活动经验。

4.强化思路分析，重视方法指导

解决数学问题，除了需要掌握并灵活运用数学知识外，还需要清晰的研究路径与明确的分析思路、合理的解题策略与有效的解题方法做支撑。无论是解决现实问题还是数学问题，首先必须思考解决问题的路径并捋清分析思路，这应该成为一种习惯。如“第16题”是基于动态探究、逻辑推理的角度计算问题，其探究路径一般为：第一步，画出并思考∠α从0°到75°变化时点A′的各种可能位置；第二步，研究点A′各种位置下△A′DE为等腰三角形时的角度关系；第三步，利用角度的数量关系求出∠α的大小。

同样地，选择合理的解题策略与有效的解题方法至关重要，不同类型的问题应该选择不同的策略与方法。本题作为填空题只需得到正确的结果，并不要求写过程。因此，准确、完整且快速地解决问题需要想象、推理与计算。事实上，该题的推理与运算过程并不复杂，关键是用足条件、操作探究与有序思维。

5.揭示数学本质，优化思维品质

数学具有严谨性、抽象性、简洁性、统一性等特征，数学学习与研究的最高层次是揭示具有一般性的、最本质的特征与规律、方法和思想。数学是思维的体操，通过数学学习，可以培养人的逻辑思维能力，提升思维品质。因此，数学教学要在揭示数学本质、优化思维品质上下功夫。

在解决问题中揭示数学本质。在解题教学中，教师要关注通性与通法，少讲技巧和所谓的模型、套路。比如“第16题”属于图形的旋转与翻折问题，其本质是变化前后的图形之间的关系属于“具有特殊位置关系的图形全等”。图形旋转后，对应线段、对应角分别相等，对应点到旋转中心距离相等；图形翻折后，同样有对应线段、对应角分别相等，对应点的连线段被折痕（对称轴）垂直平分；对应点到折痕上任意一点的距离相等。抓住这些数学本质，问题就能迎刃而解。同时，通过具体问题的解决过程，反过来又能强化对数学本质的揭示与理解。

在反思质疑中优化思维品质。直观与想象、推理与论证、质疑与反思都是重要的思维品质。以质疑与反思为例，教师要通过问题驱动学生对条件与结论、过程与方法进行质疑、探究，培养学生质疑反思的能力，从而充分发挥试题的教学价值。如“第16题”在解答后可以从以下方面质疑与反思：为何要添加“0°<α<75°”的条件？没有这个限制条件会出现什么情况？为何要强调射线CA′与AB相交？如果∠A换成其他角度情况如何？经过深入的反思质疑、探究思考的过程，不仅有新的发现，收获新的结论，更重要的是增强了数学探究能力，提高了数学思维能力，优化了数学思维品质。

（作者单位：江苏省泰州市姜堰区实验初级中学）