融合思政元素的“高等数学”课程设计与实践

［摘 要］ 探讨了如何在“高等数学”教育中将思想政治教育融入课堂教学，并以曲线拐点教学为例进行了实践和应用。“高等数学”课程作为培养学生科学素养和解决实际问题能力的关键课程，须注重学生的综合素质培养。思想政治教育的目的是培养学生的思想道德素质和社会责任感，二者的结合对学生的学习具有积极的影响。通过将曲线拐点教学与思想政治教育相结合，可以提高学生的学习兴趣和动力，培养其创新能力和实践能力，促进学科交叉和综合素养的发展。另外，从课堂引入、教学过程和结尾等方面提出了具体的教学方法和建议，以期帮助教师在“高等数学”教育中有效融入思想政治教育。

［关键词］ “高等数学”教学；思想政治教育；曲线拐点教学；学生综合素质；教学方法

［基金项目］ 2022年度广西高等教育本科教学改革工程项目一般项目A类“地方院校‘高等数学’课程思政教学改革的研究与实践”（2022JGA309）；2020年度广西高等教育本科教学改革工程项目重点项目“基于专业需求的地方高校理工类专业高等数学课程教学改革研究与实践”（2020JGZ145）；2022年度河池学院科研项目（电子信息一流学科）“基于多物理场遥感大数据融合分析的流域洪水预测和防控研究”（2022YLXK001）

［作者简介］ 欧阳云（1982—），女，江西萍乡人，硕士，河池学院数理学院副教授，主要从事应用数学研究；许敏明（1976—），男，广西崇左人，硕士，河池学院数理学院副教授，主要从事理论物理研究；肖春梅（1968—），女，广西东兰人，学士，河池学院数理学院教授（通信作者），主要从事数学教育研究。

［中图分类号］ G642.0 ［文献标识码］ A ［文章编号］ 1674-9324（2024）28-0169-04 ［收稿日期］ 2023-06-26

引言

“高等数学”在理工科学生学习中扮演着重要角色，能够培养学生的科学素养、数学思维和问题解决能力。然而，仅注重数学知识和应用难以满足社会对人才综合素质的要求。因此，将思政教育与数学教学结合已成研究热点。本文以曲线拐点教学为例，探讨了融入思政教育的“高等数学”课程对学生学习的影响。

“高等数学”是理工科基础课程，具有重要性。然而，传统的教学模式注重数学知识和应用的传授，易忽视学生思想品质的培养。近年来，高等教育强调素质教育，课程不仅须传授知识，还应培养综合素质。因此，“高等数学”课程须注重思政教育。曲线拐点是重要的知识点，涉及理论和实际应用［1-2］。通过教学，促使学生更好地掌握知识，培养创新思维和实践能力，开创新时代思政教育新局面［3-4］。

一、“高等数学”思政教学的理论基础

“高等数学”是一门重要的基础课程，是理工科学生必修的学科之一。在“高等数学”教学过程中，如何将其与思想政治教育相结合，在高等数学知识讲授中融入思想政治教育，成为当前“高等数学”教育中亟须探讨的一个重要问题。

首先，思想政治教育是一项长期系统的教育活动，其目的是培养学生的思想道德素质、创新能力等。在“高等数学”教育中应该注重对学生思想政治教育的渗透和引导，通过数学知识的学习，培养学生的思辨能力和分析问题的能力，促进学生思想的升华和发展。

其次，“高等数学”教学内容繁多，难度较大，一些学生容易陷入盲目记忆和应用知识的困境，导致思维能力退化。而思想政治教育强调的是人的整体发展，培养学生的人文素质，让学生在学习过程中保持良好的心态和态度，促进学生思维的深化和升华。

二、曲线拐点教学在“高等数学”思想政治教育中的实践与应用

在曲线拐点教学中融入思政教育对学生的高等数学学习具有重要的积极意义。本文从课堂引入、教学过程和结尾三个方面，探讨如何将思政教育渗透进曲线拐点教学。

（一）课堂引入

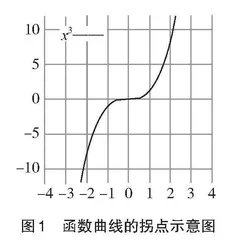
在“高等数学”教学中，教师常常会先介绍曲线的基本概念及其特殊点等相关内容，再引入曲线拐点的概念［5］。然而，曲线拐点是指曲线的弯曲方向（曲线的凹凸性）发生变化的点。这种变化可以是曲线由凸变凹（见图1），或者相反的情况。由于涉及曲线形态的突变，这一概念对学生来说可能较难理解。因此，建议教师在引入曲线拐点概念时，采用类比的方式，将其与实际生活中的工程实例联系起来，以便学生更好地理解和应用该概念。例如，可以引入港珠澳大桥的建设实例，探讨其曲线拐点的设计及应用（见图2）。这样不仅可以帮助学生理解曲线拐点的概念，同时可以将思政教育融入课堂教学中，引导学生了解精神文明建设、勇敢面对困难和挑战、推进科技创新和可持续发展等方面的内涵和重要性。

在课堂中，教师可以先介绍曲线拐点的定义和基本性质，然后引入港珠澳大桥的建设实例，探讨其曲线拐点的设计和应用。在探讨实例的过程中，教师可以引导学生思考以下问题。

1.港珠澳大桥建设面临了哪些困难和挑战？这些困难和挑战如何影响到曲线拐点的设计和应用？

2.港珠澳大桥的曲线拐点设计是如何优化桥梁的运行效率并确保车辆行驶的安全的？这些设计是如何考虑曲线拐点的位置和数量的？

3.港珠澳大桥的建设采用了哪些先进的技术和设备？这些技术和设备如何保障了桥梁的可持续发展？

通过这些问题的探讨，学生不仅可以更好地理解曲线拐点的概念和应用，同时也可以了解到困难和挑战如何促进科技创新与可持续发展，以及如何在实际生活中应用数学知识。

（二）教学过程

1.基本性质的讲解。在介绍曲线拐点的基本性质时，教师可以引导学生探讨拐点的数目、位置和性质。为此，教师可以让学生观察曲线的变化，并通过分析实际例子来说明曲线拐点的性质。另外，教师可以强调拐点的概念和定义，以及它们在数学和实际应用中的重要性。

2.思想政治教育的引入。在教学过程中，教师可以将曲线拐点的概念与思政教育相结合，引导学生思考如何将这些数学知识应用到实际生活中，为社会做贡献。例如，通过讨论道路设计中拐点的位置和数量，学生可以深入思考如何在确保道路安全和交通效率的前提下，更好地服务于社会大众。在探讨曲线拐点的基本性质时，教师可以自然地融入思政元素，使之与数学概念相辅相成，而非强行附加。以下总结了一些思政育人素材：（1）坚韧不拔的品质：曲线拐点象征着曲线中的转折点，其克服困难和挑战的过程正是培养学生坚韧不拔品质的绝佳机会。（2）科学精神：解释曲线拐点的基本性质需要深入的学科知识和严密的逻辑推理，这促进了学生科学精神和学术态度的培养，促使他们学会用理性思维和科学方法解决问题，具有对知识的求索和探索精神。（3）勇于创新：探讨曲线拐点的基本性质不仅是在传统知识的基础上重复教学，更是为了激发学生的创新意识。通过与现代技术和科技发展联系，鼓励学生探索新的思路和方法，培养他们勇于创新的能力。（4）社会责任：通过探讨曲线拐点的基本性质，我们不仅可以学习数学知识，还可以引导学生思考他们在社会中的角色和责任。就像曲线中的拐点一样，个人的成长和决策不仅对自己，也会对家庭、社会产生影响。通过思考曲线拐点与社会责任之间的关系，学生可以更深入地理解他们在社会中的作用，以及如何为社会的发展和进步做出积极贡献。（5）国家建设：以港珠澳大桥为例，探讨曲线拐点的基本性质与国家建设的联系，不仅为了让学生了解国家建设的重要性，而且能够激发他们的爱国情感。通过了解国家重大工程的背后故事，学生能够深刻理解国家建设的艰辛与伟大，进而培养他们为国家繁荣发展贡献力量的责任感和使命感。

3.案例分析。当谈到融入思政教育的曲线拐点基本性质教学时，我们可以考虑引入一个案例分析，即如何通过港珠澳大桥的建设来引导学生探讨曲线拐点的基本性质。

港珠澳大桥是世界上最长的跨海大桥，也是中国的一项重大基础设施项目。该项目在建设过程中面临了各种技术和管理方面的挑战。其中之一是如何在大桥建设过程中控制成本并确保质量。这时曲线拐点的基本性质就可以发挥重要作用。

首先，教师可以向学生介绍港珠澳大桥建设的历史和背景。然后，可以通过图表展示大桥建设成本与时间的关系，引导学生探讨成本与时间曲线的变化趋势。学生可以通过计算、分析数据和绘制图表，探究曲线拐点的基本概念和性质。

接下来，教师可以提出一些问题，如“在港珠澳大桥建设中，曲线拐点出现在哪里？”“我们如何使用曲线拐点的基本性质来控制港珠澳大桥的建设成本和质量？”以激发学生的思考和讨论，从而帮助他们深入理解曲线拐点的基本性质。

同时，教师可以引导学生探讨港珠澳大桥建设对社会和经济的影响，包括提高地区发展水平和促进人民群众的生活质量等。通过这些探讨，学生可以认识到大桥建设的意义和价值，进一步提高思政教育的效果。

综上所述，通过港珠澳大桥案例分析，可以将曲线拐点的基本性质与实际应用相联系，帮助学生深入理解这一概念，并通过思政教育的引导，提高他们的综合素质和社会责任感。

4.曲线拐点应用例题讲解。当教师在教授曲线拐点的应用解题时，可以融入思政元素。下面是一个例子：在讲解过程中，教师可以提出这样一个问题：为什么要求曲线的拐点？学生可能会认为这只是为了完成作业或考试。教师可以进一步解释，找到曲线的拐点是为了更好地理解数学背后的原理，并在实际生活中应用这个知识点。

接下来，教师可以进一步展示如何应用曲线拐点的基本性质来解决实际问题。例如，教师可以给出以下问题：假设有一辆汽车行驶在一条笛卡尔坐标系中的曲线上。汽车的速度可以用函数v（t）=t2-4t+5表示，其中t表示时间，单位是秒，v（t）表示速度，单位是米/秒。求出汽车的加速度和汽车行驶曲线上的拐点。在解决这个问题的过程中，教师可以引导学生理解曲线拐点的概念，并利用曲线拐点的基本性质来解决问题。同时，教师可以进一步讨论如何将这个问题应用到实际生活中。例如，学生可以思考如何利用这个知识点改进汽车设计，以提高汽车的经济性和安全性。

通过这样的案例分析，学生不仅可以掌握曲线拐点的基本性质和应用，还能够深入理解数学的实际意义，并将这个知识点应用到实际生活中。同时，融入了思政元素，帮助学生从更高的层次上认识到数学对人类社会的重要性和应用价值。

（三）结尾

在课堂结束前，教师可回顾本节内容并结合人生道理进行思政教育。人们常说：“人生有拐点，不要过于沮丧或得意。拐点过去，人生将面临新的境遇。”通过讲授曲线拐点的定义和性质并融入思政教育，有利于培养学生分析问题与解决问题的能力。

引导学生在实践中感受思政教育的意义。教师在曲线拐点教学中引导学生讨论港珠澳大桥的设计和建造过程，让学生了解该工程的历史背景、技术难题和社会意义。通过这种方式，学生能在实践中感受到思政教育的重要性，认识学科知识与社会实践的紧密联系。

曲线拐点教学还能培养学生的合作与创新能力。教师可引导学生进行小组讨论、实验和创新设计等活动，例如利用曲线拐点的概念设计一个能安全通过曲线拐点的交通工具，或让学生自行设计一座跨越大河的桥梁，以锻炼他们的合作与创新能力。

三、“高等数学”课程思政教学的创新与探索

（一）制定“高等数学”课程思政教学的创新策略

1.情境化教学模式。构建与现实生活相关的数学问题，将数学知识与思政教育融合，培养学生思考、探究和综合运用数学知识的能力。

2.多元文化元素。引入数学在不同国家和文化中的应用，以及数学在人类历史和文化中的地位，促进学生开放性思维和文化意识的养成。

3.现代科技手段。结合数学软件和在线交互式课件等现代科技，直观展示数学知识的应用，增强学生的信息技术素养和创新思维。

4.实践教学环节。采用项目式学习、实验室实践等方式，让学生实际应用数学知识，培养实践能力和团队协作精神。

5.思辨和创新。鼓励学生思考、质疑和创新，引导其发现数学领域中的问题和挑战，培养对未解决问题的兴趣，激发创新能力。

6.人文关怀。关注数学知识与社会问题之间的联系，探究数学在社会发展中的作用，培养学生的社会责任感和人文素养。

（二）探索“高等数学”课程思政教学的未来发展方向

1.优化课程内容和教学方法。随着教育和科技的发展，“高等数学”课程思政教学须不断优化和更新。通过开展课外实践、参与社会公益等方式，加强思政教育的实践性，注重培养学生的实践能力，促使学生将知识应用于实际问题，并提高其对社会、国家和人民的认识。

2.加强师生交流和互动。师生交流是“高等数学”课程思政教育的重要组成部分，可举办讲座、辅导活动等加强师生之间的交流和互动，促进师生之间了解和信任，以便教师提供全面的支持和指导。

结语

本文通过对曲线拐点教学在课程思政中的应用进行了探讨和分析，揭示了其在提高学生思想品质和道德情操方面的潜力及价值。

参考文献

［1］孙燮华.关于曲线的拐点［J］.工科数学，1990（Z1）：74-77.

［2］张学山.经济学中的“拐点”与数学上的“拐点”［J］.高等数学研究，2012，15（5）：29-31.

［3］刘淑芹.高等数学中的课程思政案例［J］.教育教学论坛，2018（52）：36-37.

［4］齐新社，李国，王欣，等.高等数学课程思政方法研究［J］.高等数学研究，2020，23（4）：118-119+123.