硕士课程“算法设计与分析”案例教学探究

［摘 要］ 在中国高等教育领域“双一流”建设大环境下，一流大学建设离不开一流学科建设，一流学科建设离不开一流专业和一流课程建设，而一流课程教学案例库建设为一流专业和一流课程建设提供了有力保障。“算法设计与分析”是软件工程学科专业学位硕士研究生课程教学体系中的核心课程，探索其案例教学及其建设具有积极意义。以基于割圆随机化方法的圆周率计算问题为例，构建了分割算法与近似算法相结合的原创性教学案例，结合课程中著名问题，融入思政元素，突出实践性与原创性。由此系统地培养学生发现问题、分析问题和解决问题的能力，为进一步培养应用型高级软件人才打下坚实的基础。

［关键词］ 案例教学；算法设计与分析；圆周率；割圆术；随机化方法

［基金项目］ 2024年度新疆大学研究生教育教研项目“硕士研究生课程‘算法设计与分析’精品示范课程研究”（XJDX2024YJPK15）；2022年度新疆大学研究生教育教研项目“硕士研究生课程‘算法设计与分析’教学案例库建设研究”（XJDX2022YALK11）

［作者简介］ 朱小亮（1980—），女，安徽合肥人，博士，新疆大学软件学院高级工程师，主要从事数字图像处理研究；张 涛（1976—），男，新疆乌鲁木齐人，学士，新疆大学软件学院高级工程师，主要从事人工智能与大数据研究；孙 华（1978—），女，山东烟台人，博士，新疆大学软件学院副教授，主要从事人工智能与大数据研究。

［中图分类号］ G642.0 ［文献标识码］ A ［文章编号］ 1674-9324（2024）29-0125-04 ［收稿日期］ 2023-06-12

案例建设与实践教学密不可分，在课程中引入案例教学，建立并不断丰富教学案例库，进一步深化产学研结合，为深化专业学位研究生培养模式改革，优化专业学位研究生教育结构及健全完善专业学位研究生教育课程体系，提供了可靠的理论基础。“算法设计与分析”课程作为软件工程学科硕士研究生必修的核心课程，对于学生逻辑思维能力的培养、自主创新能力的提升，具有至关重要的作用。该门课程的教学案例建设及案例教学不仅有利于激发学生的学习热情与创新的积极性，还有利于培养学生的专业实践能力，更加有利于进一步提高授课教师的教育教学水平与实践创新能力，从而有助于提高专业学位建设与研究生教育质量，促进软件工程领域学科发展与软件产业科技进步。这对于助力“双一流”建设具有举足轻重的社会意义［1-2］。

本文设计并开发了基于割圆随机化方法圆周率区间求解问题的教学案例。本案例以圆周率问题求解为导向，提出一种割圆随机化方法，即从圆以及圆外切正多边形与圆内接正多边形入手，探索圆周率取值范围，这种取值范围会随着正多边形边数的增加而使得圆周率估值区间越来越小，越来越接近精确值。在传授专业知识的同时，还将思政教育融入其中以启迪思维，根据案例背景人物祖冲之的学术生平与科研贡献事迹得出人生感悟与启示。

一、案例教学设计

本案例由案例主题与背景、问题描述、案例分析、启示以及结尾共五个部分组成。由案例背景引入主题、描述问题，围绕主题进行问题的求解与分析，最后由案例背景故事得出人生启示与感悟。

（一）案例主题与背景

古今中外，圆周率计算是个古老而又前沿的话题。最初圆周率计算是为了社会生产生活实践，后来逐渐演变成一门科学研究，发展至今天，已变成人们的一种兴趣和情怀，一种计算先进性的较量与烘托［3］。在这一过程中诞生了很多先驱级别人物，如古希腊的阿基米德，我国古代的刘徽、祖冲之等。其中南北朝时期的祖冲之做出了突出性的贡献，如采用割圆术将圆周率值精确到小数点后的第7位，比西方国家大约早了一千年，并且祖冲之还开创了圆周率的约率和密率。圆周率计算问题及其求解方法探析是“算法设计与分析”硕士研究生课程中比较著名的问题。自古以来，圆周率计算就有诸多方法，割圆术与随机投点法是其中比较经典的方法，前者体现了分割与逼近思想，后者体现了概率论思想［4-6］。本文将这两种思路结合在一起，提出一种同时采用割圆术与随机投点法来估算圆周率的区间值的方法，并以案例的形式呈现，探索一种圆周率计算问题的新思路以及研究生课程案例教育教学的新模式。

（二）圆周率计算问题

圆周率是无限循环的“超越数”，简单直观地说，圆周率就是圆的周长与其直径的比值，是计算圆面积、球形体积及圆柱体体积等几何体的重要值。无论圆的大小如何，这个比值都是固定的，常用希腊字母π表示。

（三）案例算法分析与描述

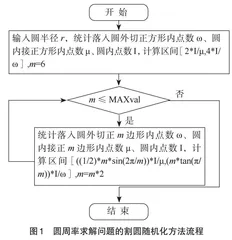
本文采用割圆法与随机投点法相结合的思路估算圆周率的区间值。根据算法流程图1得到本文算法设计与分析。令正多边形边数为m，本文算法首先求出半径为r的圆外切正m（m≥6并且m∈N）边形面积与该圆面积之比，圆内接正m边形面积与该圆面积之比；其次将这二者进行比较，估算出圆周率π的区间值。该算法流程从m=6开始不断迭代，逐步缩小其估算区间，为求解圆周率问题提供了一种新的思考方式。

正6边形（m=6）面积对应圆面积情况：首先分别观察圆外切正6边形、圆内接正6边形以及圆的相关属性。半径为r的圆外切正6边形边长为（2**r）/3、边心距为r、面积为S外=（2**r2），该外切正6边形内含有ω个随机点数；该圆内接正6边形边长为圆半径r、边心距为（*r）/2、面积为S内=3**r2/2，其内部含有μ个随机点数；该圆半径为r、面积为S圆=πr2，圆内含有Ι个随机点数。接下来，S外/S圆=（2**r2）/（π*r2）=ω/Ι⇒ π=（2*）*Ι/ω，S内/S圆=（（3/2）**r2）/（π*r2）=μ/Ι⇒π=（（3/2）*）*Ι/μ，所以得出当ω＜（4/3）*μ时，那么有（3*）*Ι/μ＜（4*）*Ι/ω⇒π∈［*Ι/μ，2*Ι/ω］。

当m=12，24，48，…时继续更替迭代。正m边形（m=12，24，48，…）面积对应圆面积情况：首先分别观察圆外切正m边形、圆内接正m边形以及圆的相关属性。半径为r的圆外切正m边形面积为S外=m*tan（π/m）*r²，该外切正m边形内含有ω个随机点数；该圆内接正m边形面积为S内=（1/2）*m*sin（2π/m）*r²，其内部含有μ个随机点数；该圆半径为r、面积为S圆=πr2，圆内含有Ι个随机点数。接下来，观察以下两个比值表达式：

S外/S圆=（m*tan（π/m）*r2）/（π*r2）=ω/Ι⇒ π=（m*tan（π/m））*Ι/ω，

S内/S圆=（（（1/2）*m*sin（2π/m））*r2）/（π*r2）=μ/Ι⇒π=（（1/2）*m*sin（2π/m））*Ι/μ，有rto=（m*tan（π/m））/（（1/2）*m*sin（2π/m））=2*tan（π/m）/sin（2π/m）=Ι/（cos（π/m））2。

当m增大时，π/m减小，cos（π/m）增大，rto减小。因为π/m→0，（cos（π/m））2→1，所以rto→1+。当ω＜rto*μ时，π∈［（0.5*m*sin（2π/m））*Ι/μ，（m*tan（π/m））*Ι/ω］。而且，随着m的增大，圆外切正m边形面积、圆内接正m边形面积越来越接近圆面积，区间［（（1/2）*m*sin（2π/m））*Ι/μ， （m*tan（π/m））*Ι/ω］减小。

（四）案例背景人物及其人生启示

圆周率先驱人物南北朝时期的祖冲之最著名的学术成就就是对圆周率的计算方面所做出的杰出贡献。纵观祖冲之一生非凡的学术成就，可以感受到的启示如下。

1.“成长环境建设”是素质教育的必修课。祖冲之的祖父是那个时代数一数二的土木工程专家，父亲学识渊博经常出席皇家礼会。因为祖辈、父辈的言传身教，祖冲之自幼养成了爱读书、勤思考的好习惯。

2.兴趣与专注是成就科研事业最好的导师。祖冲之天资聪颖、兴趣广泛，在数学、天文、机械等理工科领域表现出极高的天赋，再加上后天的专注与投入，祖冲之在以上方面均取得了卓著的成就。

3.批判性思维是科研创新的源动力，祖冲之视野开阔、文理兼长，常常从多角度、多层次、多方面分析问题，更容易发现前人学术成果中的漏洞之处，不会轻易接受存在质疑的前人观点，并且给出合理解释。反过来，这种情况又可以促进科研创新。

（五）结尾

本案例结合圆周率计算的两种方法即割圆术与随机投点法为圆周率π的近似值估算提供了一种思路。本文算法时间复杂度为迭代次数，假设迭代次数为n，那么本算法的时间复杂度为O（n）。

二、案例教学实践

经过案例教学理论分析，本案例拟实现以下教学目标。（1）正确理解割圆术与随机投点法的概念，掌握随机化方法的一般设计思想。（2）正确理解割圆法与随机投点法的特性，掌握由割圆随机化方法实现的圆周率近似值求解问题，并且能够从故事中获得人生启示。（3）深刻领悟圆周率计算的意义，客观看待圆周率求解精度对社会生产生活实践、对科学技术水平的影响，以及与高性能计算力的关系，并能够从中获得更多启发。

课堂教学及时间安排：本案例课堂教学共3学时，学时分配如下。（1）割圆法与随机投点法概念的描述与讲解为0.5学时。（2）基于割圆随机投点法的圆周率计算问题求解思路的描述与讲解为1.5学时。（3）配套思考题的讲解为1学时。另外，还要做好课前预习和课中课后讨论安排。首先是布置课前预习内容，包括割圆术与随机投点法的概念定义、割圆随机化方法实现的圆周率近似值区间估算问题及配套思考题。然后是讨论安排，课堂授课方式以教师教授为主，配合与学生线上（雨课堂）、线下互动教学，有一对一方式互动，也有一对多方式互动。课后，教师持续线上（QQ、微信）辅导学生。经过两个教学周期的课堂教学，学生评分为优秀，学生感受获益匪浅。

结语

在圆周率计算经典将其问题的基础上，将割圆术与随机投点法相结合并将其引入具体案例背景中，并倾注思想与情感，融入课程思政元素，渗入情境教学，鼓励课程交叉与思想原创。该案例教学可以为课程教学带来如下积极影响。（1）有利于进行教学改革，改革传统意义上“注入式”的教学方式。改革“注入式”教学所导致的学生学不透彻、悟不明白的缺陷，通过案例教学，引导学生学会将理论应用于实践，运用知识去解决实际问题。（2）有利于激发学生的学习积极性，将主体的学生与客体的案例有机结合，发挥学生主人翁精神，使学生在学习上化被动为主动。案例教学是一种动态开放式的教学模式，问题的答案不是封闭的、一成不变的，鼓励学生探索创新。（3）有利于提高学生善于发现问题、分析问题以及解决问题的实际能力。

案例教学可以实现将知识掌握与智能发展相结合，将教学中掌握知识点由特殊到一般、再到特殊的过程，上升到掌握普通事物的发展规律，从而提升学生认识、理解客观世界的能力。有利于培养学生形成正确的世界观、人生观和价值观，案例教学可以实现将知识传授与思想教育相结合。注重融入课程思政元素、弘扬人文精神，使得学生以正确三观学习文化知识，掌握专业技能。还有利于教师教育教学观念的转变，促进教师创新性思维习惯的养成和专业综合素质的全面提升。

参考文献

［1］李春葆.算法设计与分析［M］.2版.北京：清华大学出版社，2018：2-38.

［2］陈争光，唐永生，关海鸥，等.专业学位算法设计与分析课程案例库建设与实践［J］.高师理科学刊，2021，41（4）：102-105.

［3］刘霞.圆周率精确到小数点后62.8万亿位［N］.科技日报，2021-08-19（4）.

［4］赵晴，徐震.基于割圆术的DV-Hop全局优化WSNs节点定位算法改进研究［J］.河南理工大学学报（自然科学版），2023，42（2）：127-133.

［5］高博，陈琳，严迎建.基于TSDM的抗时间维度随机化方法研究［J］.电子技术应用，2023，49（2）：86-91.

［6］张夏禹，陈小平.基于目标的域随机化方法在机器人操作方面的研究［J］.计算机应用研究，2022，39（10）：3084-3088.

Case Teaching Research on Master’s Course Algorithm Design and Analysis： Taking the PI Calculation Problem as an Example