在画法几何课程中空间思维的教学实践

［摘 要］ 空间思维能力是学生理解三维立体结构和二维平面投影之间关系的一座桥梁。如何在画法几何教学中有效提高学生的空间思维和空间想象能力，是值得重点探索的课题。根据多年的教学实践，从授课形式、授课理念和哲学思想角度阐述提高学生空间思维的心得，认为既须鼓励学生建立起三维物体与二维平面投影的空间转化信心，也须通过融会贯通的授课方式让学生更好地理解画法几何知识体系，并传递“万变不离其宗”的哲学思想，引导学生以有限的知识来应对变化万千的三维物体的投影问题。

［关键词］ 画法几何；空间思维；画图能力；正投影法；融会贯通

［基金项目］ 2019—2022年广东省基础与应用基础研究基金项目“力致发光变色的形状记忆高分子的设计合成及其性能研究”（2020A1515010476）

［作者简介］ 黄华华（1982—），女，广东信宜人，博士，中山大学材料科学与工程学院副教授，主要从事功能高分子合成及应用研究。

引言

画法几何是理工科专业必修课程“工程制图”中最重要和最核心的部分。“工程制图”课程是一门用投影法绘制工程图样和解决空间几何问题的理论与方法的技术基础课，画法几何部分主要是研究用正投影法图示空间几何形体和图解空间几何问题的基本理论及方法［1］。简而言之，画法几何就是研究如何“由物画图，由图想物”的过程，这一过程须要把投影分析与空间想象紧密结合。所以，画法几何的学习，离不开空间思维和空间分析能力的培养。因此，在画法几何教学过程中，如何有效培养学生的空间分析和空间想象能力，是重中之重的教学任务［2］。而学生空间思维能力的提高，将令其受益终生，因此，这也是每位“工程制图”教师的教学使命。根据笔者连续担任“工程制图”课程六年授课经验，分享对学生空间思维能力培养的思考和见解。

一、引导学生，建立三维立体结构与二维平面投影的空间转化信心

画法几何研究的核心问题是如何用二维平面投影来反映三维物体。为了将三维立体结构在二维平面图形中反映出来，引入了正投影法。正是由于正投影法的引入，使三维立体结构的表达不再符合日常形象思维和感性认识而变得抽象。而空间想象能力，正是连接二维投影和三维物体之间的桥梁，如何架通这一桥梁，是诸多学生面临的关键难点，也是教学中须特别注意解决的问题［3］。

通常，在教学过程中我们会借助电脑动态图片、3D动画或者各种三维模型来引导学生理解三维立体在二维平面的投影问题［4］。但是，单纯依赖这些辅助手段，容易给学生造成听课很明白、做题却发愁的情况，因为学生课后离开了这些辅助，容易不知道如何引导自己进行空间想象。笔者通过教学经验发现，引导学生善于借助身边随处可见、随手拈来的三维实物进行空间想象，会获得事半功倍的教学效果。而且，这种引导在学生刚开始接触工程制图和画法几何时就开始展开，会让学生对学习画法几何时产生浓厚的兴趣，提高自创三维模型的积极性。例如，在“工程制图”第一次课介绍三个互相垂直的投影面构成三投影面体系的概念时，让学生寻找周围环境，如地面、正面墙壁和右边墙壁可构成第一挂角，或者把课本打开垂直放置桌面也可构成一个三投影面体系；在介绍直线与平面的投影时，引导学生采用笔、书本、三角板等通过正投影法理解特殊位置直线和特殊位置平面的投影规律；在讲解直线与平面相交或者两平面相交的遮挡关系时，让学生用笔穿过纸张或者小纸张穿过大纸张来琢磨二者的投影问题；在讲解立体投影、体与体相贯时，纸杯、粉笔盒、卷曲书本和水杯都是很好的三维实物，利用好水杯，学生能更直接地理解曲面立体的投影特点，也能更好地明白两曲面立体相交时的相贯线形成及其投影规律。因此，在课上，通过电脑动画和三维模型展示，再加上身边的三维实物，不仅活跃了课堂的氛围，提高了学生的空间想象积极性，更重要的是，帮助学生建立了三维立体与二维平面空间转化的信心。在课程后期，会看到学生很自然地借助水杯或者书本等进行空间想象，发现学生的空间思维越来越活跃，看图做题的速度越来越快。

二、融会贯通的授课理念

在画法几何介绍中，大多数课本和授课都会从点、直线和平面的投影开始讲解，接下来是简单体的投影、平面与立体相交、立体与立体相交，再到组合体。这样一个知识结构体系在教师看来是合情合理、衔接自然且富有逻辑性的。可是，对于初学该课程的学生而言，教学中知识点的衔接具有跳跃性。如果教师在授课过程中，完全照本宣科，仅仅按照点、直线、平面到立体的投影这样一个线索进行讲解，学生在学习过程中，会产生不少困惑［5］。例如，他们不明白特殊位置直线和特殊位置平面的意义，而在解决体的投影问题时，不会运用这些“特殊线”和“特殊面”来读图与画图；在简单体投影的讲解中，很难理解立体表面取点问题的重要性，而在画图时，又不能很好地运用面上取点法来作图。然而，在笔者的教学经验中，发现课堂中融会贯通的讲授方式，一方面，能让学生更好地理解画法几何的知识结构体系，另一方面，能促进学生灵活自如地运用画法几何的基础知识，而不是照葫芦画瓢式地解决二维平面表达三维物体的问题。

笔者认为，很多教师在授课中都会或多或少采用融会贯通的方法，给学生梳理知识体系，但真正将融会贯通落到实处，并不是一件简单的口头表述的事情，这需要教师熟练运用画法几何知识结构体系去读图和画图，并在教学过程中做好课程设计和方案。在这里，笔者列举以下三个例子加以说明。

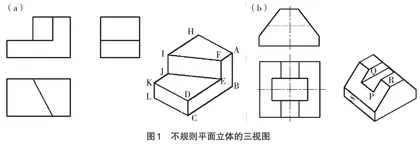
1.在讲解特殊位置直线和特殊位置平面前，展示如图1（a）三维立体结构在三个投影面上的投影，让学生观察直线IF与直线EF的投影，从而引出投影面平行线与垂直线的投影特点；观察平面AFIH与平面FEJI的投影，引出投影面平行面与垂直面的投影特点。而在讲解点、直线与平面投影后，及时运用这些投影特点，对较为复杂的立体结构投影进行分析，如图1（b），重点分析P面的投影，学会利用垂直面的投影特点，想象P在侧面投影面的投影形状。通过体的投影引出直线与平面投影，再反馈体的投影这样一个融会贯通的讲课方式，容易使学生清楚地知道点、直线与平面投影是三维模型在二维平面上投影的基础，并且培养学生从点、直线与平面投影的角度去分析三维模型在二维平面上投影问题的思维能力。

2.在讲解基本体面上取点法，尤其曲面立体的表面取点问题时，可以适当展示一些典型的组合体三视图，让学生初步明白复杂的组合体或者不规则三维物体在二维平面的投影，可归根于立体表面的取点问题，从而清楚面上取点法的重要性。如图2（a）所示，通过向学生展示被两个平面截切后的不规则圆锥三视图，指出问题的关键是把立体表面上的A、B和C点投影做出来，从而引出曲面立体表面取点方法，并在此图上展示辅助直线法和辅助圆法完成该立体的三视图。而介绍体表面取点方法后，反过来让学生独立完成如图2（b）的三视图。在图2（b）中，圆锥是水平放置的，而前面展示的体表面取点法包括图2（a）的圆锥是立起来。学生对立起来的圆锥比较容易接受，但面对水平放置的圆锥，尤其如图2（b）被截平面截切后的圆锥，部分学生会出现畏难情绪，一些学生能想象出其投影形状，但不懂如何采用体表面取点法将中间点I在俯视图中做出来。所以，需要在水平放置的圆锥上进一步展示通过辅助直线法和辅助圆法两种方法来完成体表面取点的问题。因此，通过组合体投影引出面上取点法，再反馈组合体投影这样一个融会贯通的授课方法，一方面，可以让学生重视面上取点法的学习，认真掌握基本体的表面取点方法，另一方面，能够提前培养学生对待复合体投影的正确逻辑思维和空间想象能力。

3.在讲解立体与立体相交，涉及含有内表面结构的表达或者含有内孔的体与体相交时，可以引导学生以剖视图的角度进行空间想象。在许多教材和课程安排上，剖视图是设计在《立体与立体相交》和《组合体》章节后才开始向学生介绍的。而在这里提倡，提前给学生介绍剖视图的概念，并向学生展示一些简单的剖视图，原因主要有以下三点：一是非常有助于学生解决含有内孔的体与体相交的投影问题。含有内部结构的三维物体的表达，尤其涉及含有内孔的体与体相交，对于初学者来说是一个富有挑战性的难题。如何帮助学生克服面对内部结构复杂的物体空间想象困难的问题？采用剖视图的角度进行空间想象是一个非常好的办法。引导学生在面对有内孔结构的三维物体时，假想用剖切平面剖开物体，将处在观察者与剖切面之间的部分移开，而将其余部分向投影面投射，这样学生自然而然地学会了将内部结构转化为外部立体进行空间想象。二是在具体学习《剖视图》章节时，学生也自然理解和接受剖视图的表达方式。如果没有前面的提前铺垫，许多学生会产生困惑，为什么前面涉及内部结构表达时，没有介绍用剖视图的角度去看待内部结构呢？为什么前面用虚线表达内部结构而在这里须改成粗实线呢？三是这样一个承上启下和层层递进的讲解思路，体现了画法几何知识的连贯性以及本课程融会贯通的学习理念。在笔者看来，融会贯通理念的传授，就如“授人以鱼不如授人以渔”，具有非常重要的教学意义。

三、万变不离其宗的哲学思想

在学习画法几何的图形表达过程中，我们会发现，画法几何的投影原理和概念是很少的，如何利用有限的投影原理来面对形状各异和结构多变的三维物体在二维平面上的表达，是值得我们认真探讨的课题。在画法几何中非常重要的关系就是三视图间的三等对应关系（长对正、高平齐、宽相等）和方位对应关系。这两种对应关系贯穿整个画法几何的学习，不论画图还是读图都须要运用这两种对应关系来解决三维立体结构与二维平面间的空间转化问题。因此，如何引导学生真正利用好三视图间的对应关系，来应对变化万千的三维物体的投影，也就是如何引导学生将“纵横不出方圆、万变不离其宗”的哲学思想落到实处，是画法几何教学中最重要的思想引导。

根据笔者的教学经验，要让学生在画法几何中真正体会到“万变不离其宗”的哲学精髓并自然运用，在授课过程中须注意以下两点：一是在图解过程中，教师要以身作则，经常通过动画方式，向学生逐步展示如何运用三视图间的对应关系来读图和画图。二是强调采用正确的图解思路进行解题。尤其对于已知三维物体的二视图或部分视图，须做出第三视图。首先进行空间想象，然后根据已知投影作出未知投影，最后进行反馈，确认三维物体与二维平面的表达是否一致。而进行空间想象到作投影画图，再到图形确认的过程，都离不开三视图间对应关系的运用。

结语

总而言之，在画法几何教学过程中，学生空间思维和空间想象能力的培养，是非常重要的教学目标之一。一旦学生对三维立体结构在二维平面投影空间转化的信心和兴趣建立起来，其绘图和读图能力培养则是水到渠成的事情，所以，教师应鼓励学生多动手搭建三维模型，多思考、多练习。此外，通过融会贯通的教学理念，可以让学生非常清楚画法几何的整个知识体系，真正掌握用正投影法来图示空间几何形体和图解空间几何问题的基本理论及方法，能以“万变不离其宗”的哲学思想，以有限的理论知识沉着应对生产和生活中各种三维物体的二维平面表达问题。

参考文献

［1］耿直，王闯.新工科背景下环境工程专业课程教学改革探讨：以画法几何及工程制图课程教学为例［J］.科教文汇，2022（1）：44-47.

［2］李玲，李卉.机械制图之“相贯线”课堂教学优化与实践［J］.教育教学论坛，2017（33）：134-135.

［3］曾萍.工程制图中组合体三视图的教学探讨［J］.贵州农机化，2020（1）：33-36.

［4］徐健，贺婷婷，姜杉，等.拆分式组合体模型的研发与在工程图学实践教学中的应用［J］.教育教学论坛，2017（4）：177-178.

［5］黄才华，叶喜葱.“画法几何”课程教学难点化解的研究与实践［J］.中国电力教育，2014（8）：94-95.

The Cultivation of Spatial Thinking During the Course of Descriptive Geometry

HUANG Hua-hua

（School of Materials Science and Engineering， Sun Yat-sen University， Guangzhou， Guangdong 510275， China）