“线性代数”教学改革的思考与实践

[摘 要] “线性代数”是大学数学中的一门重要课程，具有广泛的实际应用背景。“线性代数”主要面向非数学专业学生开设，其主要特点是概念较抽象、定理较复杂且计算较烦琐，学生在学习时感觉枯燥与困难。为了提升“线性代数”课程的趣味性，在教学过程中可以引入混合式教学模式、融入数学史及采用数形结合的教学方法，提升学生的学习积极性，提高学生的学习效率。

[关键词] 线性代数;混合式教学;数学史;数形结合

[基金项目] 2021年度广东工业大学校级“本科教学工程”项目“基于生活常识促进微积分教学的改革与实践”（广工大教字〔2021〕71号）;2020年度广东省“线下一流课程”项目“高等数学”（粤教高函〔2020〕16号）;2020年度“国家一流本科专业建设点”项目“信息与计算科学”（高教厅函〔2021〕7号，262531203）

[作者简介] 车国凤（1987—），女，河南信阳人，博士，广东工业大学数学与统计学院讲师（通信作者），主要从事大学数学教育与偏微分方程研究;张丽丽（1978—），女，山东青岛人，博士，广东工业大学数学与统计学院副教授，主要从事大学数学教育与复杂网络研究。

[中图分类号] G642.0 [文献标识码] A [文章编号] 1674-9324（2022）28-0098-04 [收稿日期] 2021-08-18

一、教学改革背景

2020年12月，国务院总理李克强在主持国家科技领导小组会议上提出：“推动科技创新要引导各方面把更多注意力放在加强基础研究、应用基础研究上来……着力加强对数学等基础学科发展的支持，夯实创新的基础。”[1]2021年7月，李克强总理再次强调要加强基础研究，特别要重视数学，因为数学是一切学科的基础。因此，数学学科越来越受到重视。“线性代数”作为大学数学中的一门重要基础课，是中学数学相关知识的延续，其重要性不言而喻。与中学数学不同的是，其抽象性更强，逻辑性也更强[2]。“线性代数”课程为土木、机械及自动化等几乎所有工科专业的学习奠定坚实的基础。

由于“线性代数”课程主要面向非数学类学生开设，且公式、定理等理论推导较多，所以学生学起来感觉比较吃力和枯燥。特别是近几年，“线性代数”课程改革使得课时缩减，为了完成教学任务，一部分教师只能采取“满堂灌”的教学方式，大大减少了教师与学生之间的互动，同时教学过程相对比较紧张。另外，随着科学技术及网络的发展，个别学生在课堂上走神的情形不仅是传统课堂上的打瞌睡和聊天等，而更多的是低头玩手机。尽管教师时常会走下讲台提醒学生，但这并不能从根本上解决问题。

二、教学改革措施

（一）使用混合式教学模式

混合式教学模式主要是指线上线下相结合的教学模式[3-5]。近些年，随着科学技术和信息网络的发展，很多网络教学资源可供借鉴，如中国大学慕课和SPOC等学习资源[6，7]，而且大量的学习软件可供选择，如QQ、微信、腾讯会议及雨课堂等软件。在“线性代数”教学中适当地结合一些网络学习资源和学习软件，可以很好地提高学生的学习效率。由于“线性代数”内容较多，且很多内容较抽象，学时较少，为使学生在有限的时间内很好地掌握教学内容，可以对线上线下学习内容做适当分类。需要指出的是，学习内容的分类非常重要，要在熟悉课程内容的基础上，根据教学内容和学生学情进行恰当的分类，并在教学过程中根据学生的学习情况随时做适当调整。经过初步的研讨，在概念的引入、基本性质的介绍及简单的计算等方面可以采取线上教学，如简单的行列式计算、向量的概念介绍及其运算、特征值与特征向量的定义和性质、二次型的定义等内容;对于一些比较难理解的知识点，采用线下教学，如特殊行列式的计算、矩阵的乘法、矩阵的相似对角化等内容。以雨课堂教学工具为例，雨课堂学习对网络速度要求较高，同时需要学生在手机上安装微信，教师在电脑上安装雨课堂软件。在上课之前，教师任意打开一个PPT文档，就会自动显示出雨课堂，在雨课堂慕课视频区域寻找合适的、时长适中的“线性代数”精品课程提前发送给学生预习，让学生提前了解下节课将要学习的知识点及相关内容，而且可以使学生随时随地学习，不会厌烦，达到间接督促学生预习的效果。除此之外，雨课堂还有很多其他功能值得教师运用，例如，在课前，教师可以利用签到功能快速地了解学生的出勤情况;在学习过程中，教师可以在雨课堂提前输入一些题目，课堂上邀请学生作答，之后在雨课堂直接查看班级每个学生的作答情况，相比于传统课堂提问个别学生的方式，这种线上的模式既省时间又可以提高教学效果;同时，学生可以随时发弹幕表达自己的疑问，教师可以根据学生的问题大致掌握学生的学习情况，进而适当调整;在课程结束后，教师可以根据雨课堂中的数据，详细地了解班级学生总体的学习情况及每个学生的学习状况。

（二）将数学史融入课堂

由于“线性代数”比较侧重于理论研究，内容相对枯燥，学生学习的积极性不高。为了提高学生的学习兴趣，可以将与线性代数内容相关的名人轶事穿插课堂中[8]。例如，引入早期运用矩阵概念数学家高斯的故事。高斯是一位非常著名的数学家，他在很小的时候就展现了极高的数学才华。在高斯发明自然数列求和公式之前，我们只能通过一个个数相加得出结果，运算量比较大，但是高斯在研究这个数列时，想出了一个快捷且准确的方法，这便是后来的自然数相加求和公式，这个公式为更一般的等差数列求和奠定了基础，而且高斯想出此方法时仅有9岁。更为惊奇的是，在他只有3岁的时候，就可以看出他父亲账目中的错误并将其修改。高斯在1795年进入格丁根大学学习，当时对是否选择数学专业也很不确定，鉴于他在数学上已经取得了一些成绩，最后还是选择了数学专业。事实证明，他的选择是非常正确的。他在大学前两年就在数学领域取得了很大的成就。特别是，他发明了二次互反律并解决了困扰数学家两千多年的难题：只用圆规和直尺画出正十七边形。在1798年，高斯直接转入黑尔姆施泰特大学，凭借他在数学上又取得的一个巨大突破：证明了代数基本定理，第二年直接博士毕业。高斯从上大学到博士毕业只用了四年的时间，足以看出他在数学学习上是多么出色。高斯从1807年开始就一直在格丁根大学工作，直到1855年去世。在高斯的一生中，他不仅在数学上取得了极高的成就，还在物理、天文等领域有很高的造诣。通过实践可知，在课堂上融入一些数学家与数学历史等故事，可以极大地提升学生学习“线性代数”的兴趣，同时对学生数学素养的提高也起到了很好的效果。

（三）采用数形结合的方法

“线性代数”内容比较抽象，需要很强的理解能力才可以深刻理解其中的一些内容，对非数学类学生来说是一个比较大的挑战。为了让学生更深入地理解“线性代数”中的相关内容，教师采用各种各样的方法，例如，采用实例法，将“线性代数”中的概念与已知的内容联系起来，如在讲解行列式概念的时候，先从二元一次线性方程组解的表达式讲起，由其解的形式进而给出二阶行列式的概念。在教学中发现，数形结合的方法在“线性代数”的学习中起到了很好的作用[9]。通过图表的形式把“线性代数”相关内容表示出来，既可以让学生很清晰地理解其内容，又可以加深学生的印象。下面通过列举一些例子，说明在“线性代数”学习中使用图表的重要性。

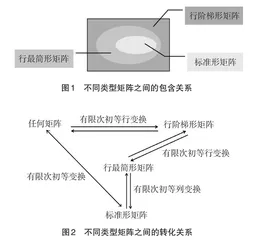
1.在介绍行阶梯型矩阵、行最简形矩阵及标准形矩阵三者关系时，可以用图1表示。从图1中可以很清晰地看出，行阶梯型矩阵包含行最简形矩阵，行最简形矩阵包含标准型矩阵。记住图1就可以很准确记住上述三种矩阵之间的关系。

2.在介绍任意矩阵、行阶梯型矩阵、行最简形矩阵及标准形矩阵之间转化关系时，可以通过图2表示。由图2可知，给定任何一个矩阵，都可以通过有限次初等行变换将其化为行阶梯型矩阵，再经过有限次初等行变换化为行最简形矩阵，最后可以经过有限次初等列变换，化为标准形矩阵，即任何矩阵可以经过有限次初等变换化为标准形矩阵，并且上述变换都是可逆的。

3.在描述矩阵、向量组及线性方程组的解之间关系时，可以采用图3表示。矩阵、线性方程组及向量组是不同章节的内容，学生学完之后不太容易厘清它们之间的关系，但通过图3，可以很清晰地看到：（1）矩阵和线性方程组之间的关系可以通过线性方程组的系数矩阵连接;（2）矩阵和有限向量组的关系可以通过矩阵的行向量组或列向量组连接;（3）线性方程组与有限向量组之间的关系可以通过方程组的系数矩阵与常数向量之间的关系连接;（4）有限向量组与无限向量组之间的关系可以通过极大无关组连接。学生在了解矩阵、线性方程组及向量组关系时，只需要记住此图形即可，既可以准确记住其主要知识点，又不容易混淆其内容。

三、总结与建议

传统的“线性代数”教学模式主要侧重于教师在课堂上传授教学内容，与学生沟通和交流比较少，很多时候教师不能准确有效地了解学生的学习效果。本文主要描述了笔者在教学过程中，为了提高教学效果所进行的一些改革举措，主要体现在以下几个方面：结合当下网络资源，在“线性代数”教学中，根据教学内容和学生学情，把教学内容分类，然后将线上教学和线下教学相结合，以雨课堂和慕课为例，说明这种混合式教学模式效果良好;由于“线性代数”内容比较枯燥，笔者尽量将与教学内容相关的数学故事穿插课程教学中，极大地提高学生的学习兴趣;由于“线性代数”中很多内容比较抽象，且课时相对较少而内容相对较多，为了让学生更好地理解和记忆相关内容，在教学过程中通过图形和表格的形式进行总结与概括。

参考文献

[1]李克强主持召开国家科技领导小组会议[EB/OL].（2020-12-07）[2021-07-14].http：//www.gov.cn/xinwen/2020-12/07/content_5567776.htm.

[2]郝志峰.线性代数[M].北京：北京大学出版社，2019：49.

[3]董丹，孙艳秋，李新.线性代数混合式教学实践[J].科技视界，2018（32）：86-87.

[4]王培.混合式教学模式在“线性代数”课堂的实践[J].教育观察，2017（6）：110-111.

[5]唐素林.浅谈混合式教学模式在法学教育中的运用[J].教育教学论坛，2021（26）：133-136.

[6]段滋明，张艳，陈美蓉，等.基于慕课网络资源的线性代数混合式教学实践[J].电子技术，2021（50）：182-183.

[7]文军，曲龙江，刘春林，等.“线性代数”课程内容优化研究及其在MOOC教学中的实践[J].高等教育研究学报，2021，44（2）：66-71.

[8]刘伟丽.浅析数学史与数学教育相结合的意义与作用[J].产业与科技论坛，2021，20（14）：155-156.

[9]王立刚，王锋，沈艳，等.《线性代数与解析几何》理论知识与MATLAB实验有机融合的探索[J].教育教学论坛，2016（16）：178-180.

Reflection and Practice on Teaching Reform of Linear Algebra

CHE Guo-feng， ZHANG Li-li

（School of Mathematics and Statistics， Guangdong University of Technology， Guangzhou，

Guangdong 510520， China）

Abstract： Linear Algebra is an important course for university mathematics， which has extensively practical application backgrounds. Linear Algebra is mainly a course for students who are not majoring in mathematics. Its main characteristics are abstract concepts， complex theorems and complicated calculations. As a result， students feel it boring and difficult to learn. In order to improve the interestingness of Linear Algebra， some reforms have been taken in the teaching process， which are mainly stated from the following perspectives： introducing the mixed teaching mode， integrating the history of mathematics and using the method of combing numbers and shapes. Some practical examples have also been listed to illustrate that the above reforms can largely improve the students’ learning efficiency. Through teaching practice， teaching reform is of great help to improve students’ learning enthusiasm and their learning efficiency.

Key words： Linear Algebra; mixed teaching; history of mathematics; the method of combing numbers and shapes