结构化统领的高三数学复习课教学实践研究

摘    要：数学是一门结构性很强的学科，而高三一轮复习课是对高中知识的拓展、延伸、归纳与整合，因此需要采用结构化教学的方式，将知识置于单元内容结构中整体理解并实施教学。教师可构建结构化统领的高三数学复习课教学模式，基于结构化进行教学分析，再进行教学的设计与实施。在此过程中，教师要重视教材内容梳理以搭建单元知识结构，关注思想方法渗透以构建教学方法结构，重构单元教学结构以完善学生认知结构，从而帮助学生认识数学知识本质，提升学生数学学科核心素养。

关键词：结构化；高三数学；复习课教学

数学是一门结构性很强的学科，从数学教学视角来看，数学的结构包括两大部分：一是数学知识结构；二是数学认知结构。前者又可分为数学知识内容结构（包括数学教材内容的编排结构、数学知识本身的逻辑结构）和数学方法结构（包括数学教材内容蕴含的方法结构、解决问题采用的方法结构）；后者即学习者的数学认知结构。对此，李昌官提出了“数学结构性教学原则”，认为应从数学的知识结构和学生的数学认知结构出发设计和组织教学，以完善和发展学生原有认知结构为目的［1］。张然然等人认为应从数学知识结构和学生原有的数学认知结构出发进行数学结构化教学［2］。二者都强调了以数学知识结构和原有数学认知结构为出发点设计教学，强调结构引领教学的重要性。

高三一轮复习课是对高中知识的拓展、延伸、归纳与整合，以强化学生“四基”，培养学生“四能”，帮助学生认识数学知识本质，提升学生数学学科核心素养为目的，教师面临教学内容较多、难度较大、复习时间紧迫的困境。因此，需要采用结构化教学的方式，将知识置于单元内容结构中整体理解并实施教学，引导学生完善数学认知结构，下面具体阐述。

一、结构化统领的高三数学复习课教学模式探索

教学模式概念的提法有很多。有学者认为：“教学过程的模式，简称教学模式。它作为教学论的一个特定概念，指的是在一定教育思想指导下，为完成规定的教学目标和内容，对构成教学的诸要素所设计的比较稳定的简化组合方式及其活动程序。”［3］也有学者认为：“教学模式从静态看是结构，从动态看是程序。”［4］

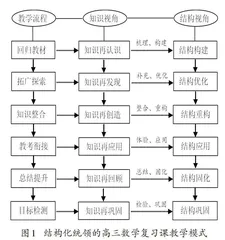
根据这些对教学模式的阐述，笔者结合之前的教学实践和研究［5］，针对复习课的教学流程，从知识发展视角和结构构建视角构建了结构化统领的高三数学复习课教学模式（如图1所示），并在实践中检验、改进，进行动态的教学探索。

二、结构化统领的高三数学复习课教学实践研究

基于以上分析，笔者以“函数的对称性和周期性”为例，进行了结构化统领的高三数学复习课教学实践。

（一）基于结构化进行教学分析

1.根据教材内容结构整合串联相关知识

对称性和周期性是函数的重要性质，是高考的热点之一。人教A版普通高中教科书《数学》必修第一册第三章第2节《函数的基本性质》设置了特殊情形的对称性内容——奇偶性，并在课后习题第13题将奇偶性推广到更一般的对称性，第五章第4 节《三角函数的图象与性质》设置了函数周期性内容，并在课后习题第19题将三角函数的对称轴和对称中心作进一步的推广。囿于教材内容编写体例与课时数的限制，在新课教学时很难将这两个不同章节的内容整合串联，系统讲解。但二者在内容发展逻辑上的联系是客观存在的，这是高三复习课整合二者知识结构、重构二者逻辑关系的事实基础。

2.根据学生认知结构设计复习教学流程

数学教学要符合学生认知过程的合理性。这节课遵循认知思维的一般规律，体现认知思维的过程性，将复习的流程设计为：回归教材（知识再认识——构建数学内容结构）→拓广探索（知识再发现——优化数学内容结构）→教考衔接（知识再应用——应用数学内容结构）→目标检测（知识再巩固——新知结构巩固）。具体步骤为：（1）复习奇偶性、周期性的概念，构建数学内容结构；（2）以第三章第2节课后习题第13题为载体，借助数形结合的数学思想方法，将奇偶性推广到一般对称性；（3）从形的角度直观切入，观察对称函数图象的周期性特征，并利用周期性定义进行代数验证，回归周期函数的概念本质，然后以第五章第4节课后习题第19题为载体，借助数形结合的数学思想方法，得到三角函数对称性的一般结论，再从整体视角重构教学的内容结构，将对称性与周期性整合、串联以形成新的知识结构和认知结构；（4）教考衔接，通过学习高考真题应用知识，应用结构；（5）总结提升，回顾这节课所学知识，总结内容知识，构建内容结构，提炼内容所蕴含的方法结构，形成新的认知结构；（6）目标检测，设置合理试题，检测目标完成情况，检验、巩固教学结构。

3.根据研究思路与方法的分析确定整体设计思路

函数是贯穿高中数学的四条主线内容之一，其研究思路与方法具有一致性与普适性。这节课中“函数的性质”是从整体上研究一般函数的性质，其研究思路和方法对于后续一类具体函数的研究具有重要的借鉴与引领作用。数形结合思想方法为不同函数的研究建立了方法上的统一性，是研究函数性质的重要方法与思路。这节课的整体设计思路遵循形→数的研究路径。一方面，由奇偶性、周期性的“形”的特征探究其“数”式结构，通过改变对称中心（轴）的位置推广到一般对称性，再探究其“数”式结构特征并验证解决第三章第2节课后习题第13题，最后推广到更一般的结论。另一方面，关于对称性与周期性的知识整合，则由图象自身具有的对称性与周期性特征猜想二者之间的关系，并用“数式”表示出来，再回归周期性定义给予代数证明，然后通过图象伸缩变换得到函数[f（ωx）]的直观图象，观察其对称性与周期性的关系，并表达成“数”的形式，通过代数推理，最终指向函数[f（x）]“形”的特征。

（二）教学设计与实施

1.回归教材——构建单元教学内容结构（知识再认识）

师：上节课我们学习了函数的单调性与最值，今天我们一起来学习函数的奇偶性和周期性，请大家回顾教材对这两个性质的阐述。

问题1：教材研究函数奇偶性和周期性的一般方法与路径是什么？

［师生活动］教师提出问题，引导学生体验奇偶性、周期性定义的研究方法（即数形结合），研究路径（即形→数）。

设计意图：回归教材，构建数学教材内容结构，探究问题研究的方法路径，把握学生的数学认知起点。

2.拓广探索——顺应单元方法路径（知识再发现）

问题2：按照这个一般研究方法与路径，下面我们进一步对教材进行挖掘与研究，请大家回顾并思考教材第87页第13题。

追问1：请大家按照由形→数的研究路径，思考并证明函数[y=f（x）]关于点P（[a]，b）对称的充要条件是：[y=f（x+a）-b]是奇函数。

［答案预设］如图2所示，函数[y=f（x）]关于点P（[a]，b）对称[⇔][f（a-x）=-f（a+x）+2b]，设[F（x）=f（x+a）-b]，由于[f（a-x）=-f（a+x）+2b]，则[F（-x）=-F（x）]。所以函数[y=f（x）]关于点P（[a]，b）对称的充要条件是：[y=f（x+a）-b]是奇函数。

追问2：对于第13题第（2）问，请大家按照上述思路，尝试解决。

［答案预设］如图3所示，函数[y=f（x）]关于[x=a]对称[⇔][f（a-x）=f（a+x）]，设[F（x）=f（x+a）]，由于[f（a-x）=f（a+x）]，则[F（-x）=F（x）]。所以函数[y=f（x）]关于[x=a]对称的充要条件是：[y=f（x+a）]是偶函数。

设计意图：通过对教材例题的研究并拓展，构建函数对称性的整体知识结构，在探究过程中充分渗透数形结合的数学思想方法，建立研究问题的数学方法结构。

问题3：观察图4，你能得到什么结论？

［答案预设］教师引导学生由图象得到如下结论。

（1）若函数[f（x）]的周期为[T]，且[f（x+a）=-f（x）]，则[T=2a]。

（2）若函数[f（x）]的周期为[T]，将函数[f（x）]的图象上任意一点的横坐标伸长（或缩短）为原来的[ω]倍，其图象每隔[Tω]长度出现往复循环，即函数[f（ωx）]的周期为[Tω]。

（3）若函数[f（x）]的周期为[T]，且[f（x+a）=f（x+b）]，则[T=a-b]。

3.知识整合——重构单元教学内容结构（知识再创造）

问题4：请大家思考教材第214页第19题，探索函数对称性与周期性的内在关联。

［答案预设］教师引导学生继续用数形结合思想方法探究二者的关系，构建如图5所示的内容结构。

然后由图象得到如下结论。

（1）函数[f（x）=sinx]满足[f（π2+kπ-x）=f（π2+kπ+x）]，其对称轴是[x=π2+kπ（k∈Z）]。

（2）函数[f（x）=sinx]满足[f（kπ-x）=-f（kπ+x）]，其对称中心是[（kπ]，[0）（k∈Z）]。

（3）函数[f（x）=sinx]满足[f（x+2kπ）=f（x）]，其最小正周期为2[π]，是其相邻对称轴距离的2倍，相邻对称中心距离的2倍，是其对称轴和与对称轴相邻的对称中心的距离的4倍。

追问1：余弦函数、正切函数也有类似结论吗？请参照上述研究路径自主探究。

追问2：更一般地，你能找到一般函数[f（x）]的对称性和周期性的哪些内在联系？

［答案预设］教师引导学生从数与形两个方面构建如图6所示的数学内容结构。

限于篇幅，此处证明过程不再展示。

设计意图：通过问题驱动学生思考、探究。及时追问，设置追问的目的是将复杂问题分解为几个思维递进的问题，帮助学生搭建认知思维“台阶”，形成新的认知结构。让学生经历利用数形结合思想方法探究性质推广的过程，能促使其扩充数学内容结构，优化数学方法结构，同时，这也能凸显函数对称性和周期性探究方法的一致性和普适性。

4.教考衔接——应用单元教学内容结构（知识再应用）

例1：（2021年数学新高考全国Ⅱ卷第8题）已知函数[f（x）]的定义域为R，[f（x+2）]为偶函数，[f（2x+1）]为奇函数，则（        ）

A. [f（-12）=0]            B. [f（-1）=0]

C. [f（2）=0]                D. [f（4）=0]

例2：（2022年数学新高考全国Ⅰ卷第12题）已知[f（x）]及其导函数f′[（x）]的定义域均为R，记[g（x）=]f′[（x）]，若[f（32-2x）]，[g（2+x）]均为偶函数，则（        ）

A. [f（0）=0]               B. [g（-12）=0]

C. [f（-1）=f（4）]      D. [g（-1）=g（2）]

设计意图：教考衔接，以高考真题为载体引导学生应用新的教学结构。

5.总结提升——固化数学单元内容结构（知识再回顾）

师：这节课我们学习了函数的哪些知识？我们是怎样研究的？

［答案预设］教师引导学生从数与形两个方面构建如图7所示的结构化知识。

设计意图：这节课旨在凸显数学教学结构的重要性，教学的过程即结构发展的过程，进行总结意在体现复习教学的整体性与联系性原则，突出数学教学结构的可操作性与发展性原则。