“复数的三角表示”内容的教材比较与教学建议

摘    要：复数的三角表示可建立复数与平面向量、三角函数、方程之间的联系，帮助学生加深对数学知识之间联系的认识.由于教材可为“教”和“学”提供学习主题、基本线索和具体内容，是实现数学课程目标、发展学生核心素养的关键资源，教师可从编排序列、问题情境、知识阐述、训练系统等维度对各版教材展开分析，梳理异同，为融合教学作铺垫.鉴于当下教学存在的问题，教师可将“复数的三角表示”视为必学内容，运用联系和整体的观点引领概念建构，借鉴整合多版教材的素材资源，启迪学生应用复数的三角表示解决问题，引导学生思维向纵深发展.

关键词：复数的三角表示；教材比较；教学建议；高中数学

高中阶段对复数的学习，除了概念和基本表示方法外，主要学习运算和运算意义，特别是几何意义.其中，用复数的代数形式进行加减运算比较方便，并且可以通过“平行四边形法则”展现加减法的几何意义，但用它进行乘除运算却较为烦琐，且不便探究乘除运算的几何意义.为此，《普通高中数学课程标准（2017年版2020年修订）》（以下简称“《课程标准》”）增加了“复数的三角表示”内容，以此简化复数的乘除运算，并直观诠释其几何意义.复数的三角表示[z=rcosθ+isinθ]（其中[r]为复数[z]的模，[θ]为其辐角）可建立复数与平面向量、三角函数、方程之间的联系，帮助学生加深对数学知识之间联系的认识，并为解决三角函数、平面几何相关问题和高次方程求根问题提供重要途径.同时，它还是学习复变函数论、解析数论等课程的必备理论［1］.

数学教材为“教”和“学”提供学习主题、基本线索和具体内容，是实现数学课程目标、发展学生核心素养的关键资源.当前，高中数学教材共有7个版本，分别是人教A版、人教B版、北师大版、沪教版、苏教版、湘教版、鄂教版，下面笔者以这7版教材中“复数的三角表示”内容作为研究对象，梳理异同，并提出教学建议.

一、教材比较

（一）编排序列

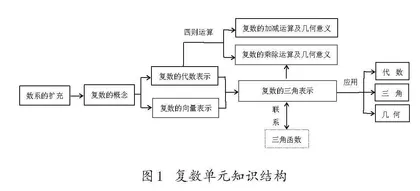
一般地，数学教材要根据数学知识发生发展的内在逻辑设计数学抽象过程，体现研究一个数学对象的“基本套路”，使教材具有内容的连贯性、逻辑的严谨性［2］.各版教材都紧跟三角函数和平面向量编排复数内容，具体册别位置不一（人教B版编排在必修第四册，鄂教版编排在必修第三册，其余版本编排在必修第二册）.在复数知识内部，各版教材都将“复数的三角表示”接续于“复数的概念与几何意义、四则运算”等传统内容之后，且独立成节.这样的编排沟通了复数与平面向量、三角函数等数学分支的联系，利于学生建构内部有机关联、衔接自然流畅、功能良性互补的复数单元知识结构（如图1所示），增强对数学知识整体性的认识.

（二）问题情境

情境为数学教学提供原动力，为数学知识应用提供场景，而作为教学手段的问题提出，则具有促进学生知识理解、提高学生问题解决能力、激发学生创造力的功能属性和价值取向［3］.数学学科核心素养通常就是在综合化、复杂化的情境中，通过学生与情境、问题的有效互动生成的.《课程标准》提出，教材编写应遵循学生认知规律，创设合适的问题情境，设计有效的数学学习活动，展示数学概念、结论、应用的形成发展过程，帮助学生把握数学内容的本质.

该节的首要问题是：如何引导学生发现和提出“复数的三角表示式”这一问题？从知识基础看，前面已经建立了复数与向量坐标的联系.此外，在三角函数中学生研究过“水车模型”，并通过证明得出：如果角[α]终边上任意一点P（x，y）（不与原点重合）到原点的距离为[r]，则[sinα=yr]，[cosα=xr].这些都为用三角函数表示半径为[r]的圆上某点的坐标做好了准备.基于此，人教A版教材设置“探究”栏目，引导学生展开学习活动：首先用模[r]表示向量的大小，然后借助图形引入辐角[θ]刻画向量的方向，再利用[a=rcosθ]，[b=rsinθ]，最终推导出复数的三角形式.该设计基于知识的“生长点”和学生的“最近发展区”，注重激发学习动机，循循善诱，详尽具体，利于学生领悟数学基本思想、积累基本活动经验.人教B版、沪教版、苏教版、鄂教版教材创设了与人教A版教材基本相同的问题情境导入新课；北师大版、湘教版教材则开门见山地给出了复数的三角形式，简明直白.

（三）知识阐述

1.复数乘法的三角表示及其几何意义

若[z1=r1cosθ1+isinθ1]，[z2=r2（cosθ2+isinθ2）]，由复数的乘法法则及两角和的正弦、余弦公式，得[z1z2=r1r2][[cosθ1+θ2+isinθ1+θ2]].可见，三角形式下的复数乘法就是辐角相加、模长相乘.

各版教材都详细推导了复数乘法运算的三角表示，并阐明了其几何意义.此外，沪教版教材进一步明确：一般地，把复数[z1]乘任意一个复数[z2]，在几何上就是对[OZ1]作两个变换的合成，即先伸缩再旋转，或者先旋转再伸缩，且这两个不同顺序会得到相同的结果.人教A版教材还设计了旁白：“你能解释[i2=-1]和[-12=1]的几何意义吗？”意在让学生借助复数乘法的三角表示及其几何意义，从几何角度深化对熟悉的代数运算的认识.

2.复数除法的三角表示及其几何意义

设[z1=r1cosθ1+isinθ1]，[z2=r2]（[cosθ2+isinθ2]），[z2≠0]，则[z1z2=][r1r2][[cosθ1-θ2+isinθ1-θ2]].其常见证明有转化法和共轭法.转化法利用除法运算是乘法运算的逆运算，结合“配凑”得出结论，运算简洁；共轭法则利用共轭复数和“分数”的性质推证结果，学生容易想到.人教A版、沪教版、湘教版教材采用转化法，人教B版、北师大版、苏教版教材选择共轭法，鄂教版教材仅呈现结论而未呈现推导过程.

对于复数除法的三角表示的几何意义，各版教材普遍着墨较少.人教A版教材设计了探究活动，启发学生类比复数乘法的三角表示的几何意义猜想结论，没有给出答案.人教B版教材提示“类似地，由此还能得到两个复数相除的几何意义”，并举例说明：任意一个复数除以[i]，就相当于把这个复数对应的向量绕原点按顺时针旋转[π2]. 其他版教材未提及复数除法运算的三角表示的几何意义.

3.复数乘方、开方的三角表示及其几何意义

若[z=rcosθ+isinθ]，则[z2=][r（cos[θ]+isin[θ]）]2=[r2cos2θ+isin2θ]，将[z]的次数推广至[n]，就得复数的乘方公式[[rcosθ+isinθ]]n=[rncosnθ+isinnθ]，即棣莫佛定理.开方是乘方的逆运算.各版教材“复数的三角表示”内容中乘方与开方编排统计如表1所示.

由表1可知，各版教材复数乘方与开方的编排差异较大.例如，沪教版教材编写了独立的一节“三角形式下复数的乘方与开方”，在正文中推导了复数乘方、开方的三角表示，并辅以适量的例题和习题.人教A版、人教B版、湘教版教材借助“探究与发现”等栏目或习题进行了一般性结论的探讨.其他版教材通过具体习题渗透复数的乘方与开方运算，未呈现一般性公式.

（四）训练系统

《课程标准》要求“整体设计习题资源，提高习题的有效性，科学、准确地把握习题的容量、难度”.数学教材中，学习训练系统主要由例题和习题组成.其中，例题具有示范引领、揭示方法、思维训练、文化育人等功能，习题则是为复习和巩固新知识、训练应用知识解决问题而设，一般包括小节后“练习题”、大节后“习题”和章末“复习（参考）题”.训练系统作为教材的重要组成部分，其选择、布局、数量等都影响着数学学习质量.各版教材“复数的三角表示”内容各类题目数量统计如表2所示.

结合表2可知，各版教材例题和习题设计有三个特征.其一，从数量来看，均较为充足，但不均衡.其二，从梯度来看，设计富有层次性与探索性.例如，人教A版教材按题目功能将习题和复习（参考）题细化为“复习巩固”“综合运用”“拓广探索”三个等级，而“拓广探索”对学生的数学阅读、数学理解、数学表达、数学创新能力提出了较高要求，弹性化的设置为不同潜能的学生提供了发展空间.其三，从问题情境来看，情境真实多样，体现学以致用.例如，人教B版教材习题10-3C第2题探求方程[xn=z]的根，湘教版教材复习题三第12题讨论旋转、伸缩等几何变换.

综上，各版教材均按照《课程标准》要求，精心编排了“复数的三角表示”内容，力图适教利学.在编排顺序方面，凸显知识间的联系；在问题情境方面，注重铺设适切的情境，设计问题（链）引导学生展开探究；在知识阐述方面，着力阐述运用三角形式进行复数乘除运算的优越性，重点突出，详略得当；在训练系统方面，采取步步为营、分门别类、螺旋累进的方式编排例题和习题，注重题目的示范性、层次性和探索性.同时，各版教材在体例结构、内容处理等方面各有倾向和风格，突出了“遵循国家标准、尊重认知规律、体现数学特点、彰显版本特色”的要求.

二、教学建议

当前，“复数的三角表示”的教学效果不容乐观.例如，受高考命题倾向影响，广大师生普遍对复数单元较为轻视.虽然《课程标准》已将其增列为选学内容，但很多教师仍将“选学”等同于“不用学”，常以教学时间紧张为由，直接取消了对其的教学，或者即使开展教学也是蜻蜓点水般一带而过，导致很多学生一知半解、认知混乱.另有部分教师缺乏明晰的指导思想来引领这一内容的教学，使学生对概念建构不得要领，应用三角形式解决问题更无从谈起.为此，笔者提出如下建议.

（一）将“复数的三角表示”视为必学内容

首先，复数的三角表示意蕴丰厚、思想深邃、应用广泛、影响深远.主要体现在：（1）复数的三角表示本质上是用有序实数对（[r]，[θ]）确定复数，同样表明了复数是一个“二元数”，它扩张了复数的表征方式，丰富了复数的内涵；（2）利用复数的三角表示处理乘除运算动能强大，三角形式下的复数乘除运算就是模长的乘除和辐角的加减，对应平面向量的旋转和伸缩，运算法则简单易记，几何意义鲜明生动；（3）复数的三角表示可以产生广泛联系，在平面向量、三角函数和平面几何等领域应用广泛，这些应用不仅蕴含着丰富的学科知识和技能，更有许多重要的思想方法和精神，可为教学提供宝贵素材和思想启迪［4］.

其次，复数的三角表示的教学操作性较强.主要依据有：（1）认知基础方面，学生已经学习了用角[θ]终边上的点P（x，y）表示三角函数，并建立了复数与向量坐标的联系，这些为学习三角表示提供了理论基础；（2）课时保障方面，《课程标准》为复数的三角表示设置了足够的课时；（3）实践反馈方面，教育部基础教育二司组织的专项调研显示，一线教师普遍有“增加复数的三角表示”内容的意愿［5］.

再次，多个国家已把三角表示列入复数必学内容.例如，俄罗斯数学教学大纲规定的必学复数内容有“复数、复数的几何解释、复数的实部和虚部、模和辐角、复数的代数表示形式和三角表示、复数在不同表示形式下的算术运算、共轭复数、复数乘方、代数基本定理”，法国数学课程标准中的复数内容有“复数、复平面、点的坐标、复数的实部和虚部、复数的共轭、复数的模和辐角、商的模和辐角、[eiθ=cosθ+isinθ]的写法、实系数一元二次方程的复数解等”［6］.

综上，从内容重要性、教学可行性和国际借鉴考虑，笔者认为一线教师可按必学内容对待“复数的三角表示”，尽量让所有学生都必选，同时对学习难度加以限制.

（二）运用联系和整体的观点引领概念建构

自诞生之日起，复数就与几何、向量、三角函数等数学分支存在天然的、深刻的、丰富的联系.例如，虚数早在16世纪就已萌生于三次方程求根问题，但直至1832年，高斯给出了复数及其运算的几何解释，复数才有了“合法”地位.突出复数的表示和运算的几何意义，从几何的角度认识、理解复数及其运算，是贯穿复数单元的一条主线.《课程标准》把复数置于“几何与代数”主线之下，也体现了这样的意图.正如克莱因所提倡的，“应当把复数解释为所熟悉的数的概念的扩张，避免任何神秘感.首要的是应当使学生立刻对复平面上的几何作图说明形成习惯”［7］.复数有代数形式、三角形式、指数形式等多种表示法，本质上说明复数有多种“化虚为实”的途径.