基于核心任务的单元复习教学与思考

摘    要：核心任务是确定学习目标及组织学习材料的依据，而选定核心任务的依据是单元核心内容.基于核心任务进行单元复习教学，可有效引导学生解决问题、积累经验、建构知识网络、发展思维能力与问题解决能力.在具体教学中，教师需要明确核心任务的一般表现方式，然后以核心素养为统领，并基于核心任务设计高质量的问题链，注重设置开放性问题以促进主动复习，设计变式问题以促进思维发展，引导学生循序渐进地进行探究，进而达成深度理解，提升核心素养.

关键词：核心任务；单元复习教学；初中数学

在日常的单元复习课中，有的教师采取知识梳理加例题讲解的形式，有的教师将作业本典型错题的订正分析当作单元复习，有的教师以单元中的专项内容小专题替代单元复习.这样并不能有效发挥单元复习课的价值.单元复习课具有如下作用：对知识查漏补缺；呈现新知与旧知在知识网络扩展中对单元内容的结构化关联；引导学生进一步感受重要的数学思想方法，促进知识经验迁移，发展高阶思维能力.笔者认为，根据单元核心内容确定核心任务，并基于核心任务开展单元复习教学，能促进学生的深度理解，培养学生的核心素养.

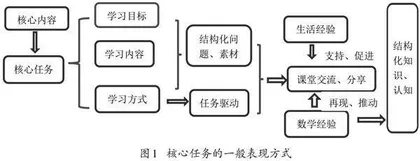
一、核心任务的一般表现方式

核心任务是确定学习目标及组织学习材料的依据，而选定核心任务的依据是单元核心内容.单元核心内容是学生必须掌握的知识、技能以及重要的思想方法，它反映知识的本质属性与共性，能帮助学生建立知识的内在关系，建构知识网络体系［1］.因此，在解决核心任务的教学过程中，单元核心内容的价值能够得到实现.在解决核心任务中实现单元核心内容价值.核心任务的一般表现方式如图1所示.

基于核心任务的单元复习教学，以发展核心素养为最终目标，通过问题链的驱动，引导学生解决问题，积累经验，建构知识网络，发展思维能力和问题解决能力.

二、基于核心任务的单元复习教学流程

基于核心任务的单元复习教学需要设计高质量的问题链，以引导学生循序渐进地进行探究，巩固对整个单元知识的理解和掌握，加深各知识间的内在联系，进而形成新的知识群.问题链中的问题可驱动学生深入思考、建构知识，并在解决问题的过程中积累活动经验、体验数学的基本思维方法，这需要教师在课堂中给学生“冷静思考的时间”和“充分表达的机会”［2］.问题链的设计需要选择适切的问题起点并确保其有良好的延展性，能使学生在数学思维方法的引导下生成问题，将学习活动引向深入.而在单元复习教学中的概括反思环节，教师还需设计更具普遍性、周延性的问题，使学生对这一主题的内容理解更为深刻，促进知识的迁移，提升问题解决能力，达到相应的核心素养目标. 基于核心任务的单元复习教学流程如图2所示.

三、基于核心任务的单元复习教学实践

下面以“等腰三角形”复习为例，具体阐述基于核心任务的单元复习教学.

（一）确定“等腰三角形”复习教学的核心任务

在复习教学中，教师可按以下路径确定核心任务：根据主题单元复习内容，梳理出核心概念及关键性质，同时注重本复习内容在整个数学知识体系中的地位与作用.等腰三角形是学生学习《三角形的初步知识》后系统研究的第一个特殊图形，学习过程中已建构基于三角形基本要素及相关要素的视角研究图形的性质、判定与应用的方法，但对图形轴对称性与要素性质之间关联与本质的挖掘还比较生疏.而图形的轴对称性是研究几何的方式之一，基于轴对称视角、利用轴对称变换解决问题在整个几何学习中有重要的作用.因此在“等腰三角形”复习教学中将“基于轴对称性研究边角性质”作为核心任务，是合理与必要的，具体如图3所示.

为充分调动学生对复习课的积极性及提高复习效率，笔者采用开放题、变式题串联整节课教学.设计开放题的目的是促使全体学生参与课堂.整节课的复习落脚于“等腰三角形性质的应用”，本质聚焦“等腰三角形的轴对称性”，以“分—总—分”结构引导学生由特殊到一般地进行探究.

（二）学习目标与重难点

学习目标：（1）通过解决等腰三角形两腰上动点位置变化过程中的一系列问题，复习巩固等腰三角形的性质与判定、三角形全等的判定方法以及轴对称图形的性质与应用；（2）积累证明线段相等的方法，掌握由特殊到一般以及转化的数学思想方法；（3）发展推理论证、几何直观等核心素养.

重点：等腰三角形的轴对称性.

难点：由轴对称性构辅助线探究角关系.

（三）教学实施

问题1：用尺规作一等腰三角形，说明作图依据.

［师生活动］教师投影学生的正确作图，由学生解说作图依据.

设计意图：作图是学习几何的最有效方式之一.在作图过程中，学生需要提取相关概念、性质及判定方法，并有序地动手操作输出.要求学生说出作图依据，则能有效地促进其对等腰三角形定义及中垂线性质的理解和巩固.

例1：如图4，等腰三角形ABC中，AB=AC，O是BC的中点，点D，E分别是两腰上的动点.当OD⊥AB，OE⊥AC时，你能得到哪些结论？

追问1：这些结论分别是根据什么性质获得的？

追问2：连接线段AO，还能得到哪些结论？为什么？

追问3：你能对上述结论分类吗？

追问4：怎样证明OD=OE？

追问5：这些结论成立的原因是什么？

设计意图：开放设问，让不同程度的学生均能参与课堂，提高学生学习的积极性.该问题起点低，点D，E的位置关系比较特殊，学生易通过三角形全等得到线段、角度的关系，复习等腰三角形边、角、线的性质.OD，OE与腰垂直，隐含点D，E关于等腰三角形的对称轴成轴对称，因此易归纳这些线段及角度的数量关系由等腰三角形的轴对称性决定.通过特殊位置关系背景下对几何研究对象的性质梳理及分类，可以引导学生养成有序观察几何对象的思维方式，明晰几何对象的研究路径，发展几何直观及推理能力等核心素养.

变式1：等腰三角形ABC中，若移动点D，E在两腰上的位置，满足OD平分∠AOB，OE平分∠AOC时，那么，点D和点E关于直线OA成轴对称吗？请说明理由.

设计意图：此变式不再聚焦对应背景下的边角关系，而是直接探究动点D，E与对称轴的轴对称性，要求学生根据“例1”积累的经验，感受在变化过程中不变性所满足的条件.将条件变为角平分线，隐含两个动点关于等腰三角形的对称轴成轴对称时，需要满足对应角度的数量关系.根据轴对称性的定义，转化为证明对应三角形全等，引导学生进一步感悟——点在运动过程中，线段、角的等量关系可以转化为等腰三角形的对应点的轴对称性.

问题2：等腰三角形ABC中，移动点D，E在两腰上的位置，若点D和点E关于直线OA成轴对称，需满足什么条件？请说明理由.

追问1：还有其他条件吗？为什么？

追问2：你能归纳等腰三角形两腰上的动点关于对称轴成轴对称时需满足的条件吗？

设计意图：通过对特殊位置时两腰上点D，E的关系与等腰三角形轴对称性间的联系，归纳任意等腰三角形两腰上动点成轴对称时需满足的条件，并感受由特殊到一般的数学思想方法在探究问题中的作用.通过追问揭示问题本质，帮助学生认清变化中的不变性.

变式2：等腰三角形ABC中，移动点D，E在两腰上的位置，若OD=OE，则∠ADO与∠AEO需满足什么条件？请说明理由.

设计意图：变式2改变问题条件，进一步引导学生深度思考，动点D，E移动速度不一样时，相同时间内所行路程不等，因此会出现点D，E关于直线OA不对称的情形.此时如何引导学生用∠ADO与∠AEO刻画数量关系是解决这个问题的难点.视角一，“基于等腰三角形轴对称性”性质应用，将点E对称到另一腰上的点F，可证∠ADO与∠AEO互补.视角二，由“例1”两腰上高垂直的经验，转化为证明OD，OE所在直角三角形全等，得到角的关系.视角三，利用特殊位置关系（均垂直腰时得到两角和为180°）.这可使学生在解决问题的过程中，积累添加辅助线的经验，培养构造轴对称解决问题的能力，拓展思维深度，发展高阶思维.同时，此变式也能很好地佐证“边边角”无法证明两个三角形全等的事实.

问题3：回答下列问题：（1）这节课复习了哪些知识？（2）是按怎样的路径对等腰三角形的轴对称性进行研究的？（3）证明两条线段相等有哪些常用的方法？（4）在解决问题的过程中运用了哪些数学思想方法？

师生在共同回答上述问题的过程中形成这节课的板书，具体如图5所示.

设计意图：引导学生厘清知识的内在逻辑及内在关系，形成数学知识、学习方式以及思考方式的结构化，凸显核心任务下的知识建构过程，即研究问题时需遵循由特殊到一般、由浅入深的思路，解决问题时则需化繁为简，将复杂问题分离出基本图形，利用基本性质解决的策略方法.

四、基于核心任务的单元复习教学反思

在基于核心任务进行单元复习教学的实践中，笔者有如下反思.

（一）设置开放性问题，促进主动复习

开放性问题，是指条件开放、结论开放、解决策略开放的问题.在复习课中设置开放性问题，能体现复习任务的自主性，充分激发学生探究、解决问题的欲望，使不同层次的学生都根据自己的认知积极参与课堂，有效反馈学生在运用已学知识解决问题时的差异性，从而有助于教师精准诊断学生对已学知识的掌握情况，提高复习教学的效率.同时，在解决开放性问题的过程中展现不同层次学生的答案，让学生相互补充、辨析、完善，达成深度复习.

如对“例1”的开放设问“你能得到哪些结论”，学生在梳理结论的过程中，可充分激发已有的学习认知，达成对等腰三角形基本概念的复习与简单应用.在此过程中，教师板书学生的回答，引导学生观察并对它们有序归类，渗透几何图形研究的一般方法与路径，可优化学生的思维品质.可见，改变提问方式，以开放性问题为任务驱动，既能使学生在解决问题的过程中达成对基本概念性质、判定的复习，又能引导学生主动关联其他相关内容，还能为引出核心任务作铺垫，可谓一举多得.

（二）设计变式问题，促进思维发展

郑毓信提出变式教学的指导思想是“变化之中求不变，求变以突出蕴含的不变因素”及“不应求全而应求变，不应求全而应求联”［3］.设计变式问题时，要关注如何变以及变什么等，把握问题的数学本质及知识关联，明晰变式方向，形成高立意、低起点、层次递进、内涵一致的问题链.基于核心任务的问题与变式设计要关注核心素养和结构化.层次递进、结构化的变式问题，是学生思维支持和干预的切入点.通过问题启发，教师以有针对性的引导，让学生感受到联想的起因、联想线路的规律性，体会这些知识、结构和方法是如何联系的［4］.在此过程中，教师也可关注到不同思维学生在课堂中的不同表现，帮助学生在解决问题的过程中发展思维.

如在以“基于轴对称性研究边角性质”为核心任务的“等腰三角形”复习教学中，教师引导学生在解决两腰上点对称的问题中，掌握“性质与轴对称性”之间是如何关联的，从而实现新旧知识之间的关联与迁移，并在解决“变式2”的过程中，发展学生的逆向思维能力，促进学生思维进阶.这样的教学可以达成由“整体建构实现内容结构的一致性，关联建构实现核心素养的一致，分层解决实现思维发展”的目标.

总之，基于核心任务的单元复习课教学，应依据单元核心内容确定单元核心任务，建构核心任务的表现方式，关注学习材料的结构化，设计相应的问题链，注重问题设置的开放性，并通过整体建构、分步实施推进课堂教学，使学生达成对知识的结构化认知，学会迁移运用，发展思维品质，最终提升核心素养.

参考文献：

［1］张优幼.单元复习课核心任务的内涵与实践探索［J］.教学月刊·小学版（数学），2023（11）：12-17.

［2］唐恒钧，张维忠.数学问题链教学的内涵与特征［J］.教育研究与评论（中学教育教学），2021（1）：8-12.

［3］郑毓信.变式理论的必要发展［J］.中学数学月刊，2006（1）：1-3.

［4］程华.数学课堂思维教学若干问题的思考［J］.数学通报，2018（3）：26-29，52.

*本文是浙江省教育科学规划课题“指向初中生核心素养的数学变式教学研究”（课题编号：2020SC252）的阶段性研究成果.