基于“教—学—评”一致性的单元起始课整体教学探索*

摘    要：基于“教—学—评”一致性实施单元起始课整体教学，需要精准分析学情、合理确定目标，锁定目标策略、预设教学流程，问题串联驱动、过程评价伴随.在实施教学前，教师先要分析课标、教材、学情并整体思考教学内容要求，整合教学内容要求并科学制订课时学习目标，再选择教学策略以促进目标达成，最后针对目标达成以制订评价方案，建构方法路径并预设教学流程.实施教学时，教师需要在整体建构的基础上把学习目标分解为一个个学习任务，通过活动设计、问题驱动把学习任务转化成学生核心素养发展的要求.

关键词：“教—学—评”一致性；单元起始课；整体教学；初中数学

《义务教育数学课程标准（2022年版）》（以下简称“《义教数学课标》”）指出：“单元整体教学设计要整体分析数学内容本质和学生认知规律，合理整合教学内容，分析主题—单元—课时的数学知识和核心素养主要表现，确定单元教学目标，并落实到教学活动各个环节，整体设计，分步实施，促进学生对数学教学内容的整体理解与把握，逐步培养学生的核心素养.”在该理念的引领下，单元整体教学受到高度重视.但如何让理念落地？有专家指出，为在教学中达成基于核心素养的数学课程目标，要对学生数学核心素养的发展作出评价，还要在《义教数学课标》的基础上，进一步结合数学课程内容，对数学核心素养的内涵进行深入、细致且具体的解读，使之成为可操作、好落实、能评价的行动指南［1］.2023年苏州市以“圆”的单元起始课作为初中数学赛课课题，引发了很多教师对单元起始课整体教学的深度思考.下面，笔者根据课堂教学实践阐述如何基于“教—学—评”一致性进行整体教学.

一、精准分析课标、教材、学情，合理确定目标，奠定实现“教—学—评”一致性的教学基础

“教—学—评”一致性要求教师精准分析课标、教材、学情，对教学内容要求作整体思考，并科学制订课时学习目标.

（一）分析课标、教材、学情，整体思考教学内容要求

1.从课标要求的角度理解单元知识

圆是一种基本的平面图形，是描述现实世界的重要几何模型.在《义教数学课标》中，“圆”是一个核心概念，属于“图形与几何”领域，主要从对称性的角度，采用类比、数形结合的思想方法研究圆及其相关概念、性质，理解点与圆、直线与圆以及圆与三角形、四边形等图形的关系.

2.从核心概念生长的角度理解学习内容

这节课是苏科版义务教育教科书《数学》九年级上册第2章《对称图形——圆》的章首课.核心概念“圆”是该章学习的起点和基础，同时为后续进一步研究圆的相关问题奠定基础.这节课具有开篇定局的作用，课本内容基于摩天轮转盘、“圆，一中同长也”等图片、文字信息，引导学生用数学的眼光发现圆的基本特征，归纳、形成圆的概念和性质，用数学的思考建立圆与相关的线、弧、角、多边形的联系，明晰点与圆、直线与圆的位置关系，整体建构，形成知识体系.

3.从最近发展区的角度理解学情

学生在小学时已经学习了圆的相关知识，初步具备了研究圆的经验，能够认识圆心和半径，能够初步感知圆是描述现实世界的重要几何模型.在相关知识的学习过程中，学生已经经历了一些利用圆的知识解决实际问题的活动经验，如能够计算圆的周长和面积.而经过初中阶段前期的学习，学生又具有了一定的研究几何图形的经验和能力，这就为进一步学习圆的知识奠定了学习基础.

4.从核心素养发展的角度理解教学方法

课堂教学需要基于学生原有的知识基础和数学活动经验，以学生原有的数学知识体系为基础，从现实生活情境和数学文化情境出发，引导学生做到：（1）用数学的眼光审视圆的世界，如借助已有的经验尝试用棉线画圆，通过动手操作，比较、感悟，再认识圆的基本特征，发现本质的数学规律，生成圆的概念；（2）用数学的思维思考圆的世界，如经历用数学的语言表达圆的概念及其相关对象关系的过程，提升学习圆的兴趣；（3）在空间观念的基础上建立几何直观，提升数学抽象能力和推理能力，充分认识到圆是描述现实世界的重要几何模型，进而建立研究圆的相关内容的知识体系、学习方法体系，发展审美情趣和数学核心素养.

（二）整合教学内容要求，科学制订课时学习目标

清晰的目标是“教—学—评”一致性的前提和灵魂［2］.在整体分析“圆”的本质的基础上，笔者根据学生的认知规律，合理整合教学内容，明确“圆”主题单元的数学知识和核心素养主要表现，进而确定了这节课的教学目标以及重难点.

教学目标：（1）通过情境，发现对象，激活圆的学习经验，抽象概括生成圆的概念，学会用数学的眼光审视圆的世界；（2）动手操作，自主探究，发现点与圆、直线与圆的位置关系，初步感悟用类比、对称变换、数形结合等数学思想方法研究圆，尝试用数学的语言表达圆的世界；（3）完善认知，建立体系，形成研究圆的章节结构，培养大胆想象、勇于探索、积极创造的数学精神，发展几何直观、数学抽象和空间观念等核心素养.

重点：探索圆的定义与性质，建构圆的知识体系，初步感悟研究圆的数学思想方法.

难点：形成研究圆与关联对象的思考方法.

二、锁定目标策略，预设教学流程，开启实现“教—学—评”一致性的教学通道

《义教数学课标》指出：“在具体现实情境中，学会从几何的角度发现问题和提出问题，经历用几何直观和逻辑推理分析问题和解决问题的过程，培养应用意识和创新意识，提升几何直观、空间观念、抽象能力、推理能力等. ”这表明，根据学生的素养行为表现评价学生核心素养的达成情况，已经成为教学的必然要求.因此，教师需要积极探索课堂学习效果评价表的设计，以有效评价学生对知识技能的掌握、基本思想的把握和基本活动经验的积累情况，考量学生发现问题、提出问题、分析问题、解决问题的能力，从而客观公正地评价学生核心素养的形成和发展.

（一）选择教学策略，促进目标达成

1.通过问题导学，揭示知识联系

问题是数学的心脏.在这节课的教学中，笔者充分体现《义教数学课标》在“前言”中提出的“坚持问题导向”原则，充分挖掘教材中的素材，通过创设问题情境，设计串联问题，按照“情境+问题串”的方式组织学习活动.这节课共设计5个任务、5个活动、7个问题，通过问题的解决揭示知识点之间的关联，体现研究几何对象的一般思考.

2.整体生长生成，形成结构体系

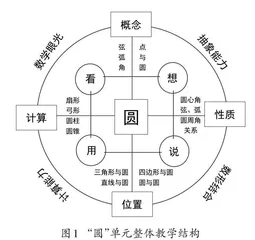
由单元核心概念“圆”统领的研究内容很多，那么应该怎样研究，研究哪些内容，采用什么思想方法研究？笔者着力知识的生长与生成，引导学生先从圆的概念出发，生发出弦、弧、圆心角、圆周角等概念，再研究它们之间的关系，生成弦、弧、圆心角之间关系、垂径定理、圆周角定理，并由此发现点与圆、直线与圆、多边形与圆、圆与圆的位置关系，从而使学生在已有知识的基础上自然研究与圆相关的扇形、圆柱、圆锥等图形的计算问题，以及小概念之间的相互关联，最终形成清晰的逻辑体系.在相关内容的研究上，笔者引导学生采用类比、数形结合、分类讨论等数学思想方法，并按照“知识要点—思想方法—核心素养”的逻辑思想，统整形成了单元整体教学结构（如图1所示）.

3.创新思考问题，力求思维进阶

怎样实现单元整体教学的创新？笔者积极尝试，通过创设各类情境，让学生自己发现圆的特征，类比归纳圆的概念，与圆相关的概念均由学生自己提出来、自己下定义.然后，笔者引导学生系统思考，全局考虑问题，创新地提出圆与点（直线、角、三角形、四边形、多边形、圆）之间的位置关系，进而采用数形结合的方法开展初步探索.最后，笔者引导学生纵向思考、横向联系，分析图形组成要素之间的关联，发现一般性结论，开展求线段、求角、求弧长、求面积、求体积等问题的研究.在此过程中，学生由表象到内涵本质，思维层次不断加深，体现发现的快乐，实现思维的进阶.

（二）针对目标达成，制订评价方案

教学目标不仅是教师教的方向，也是学生学的标杆，还是学生学习效果评价的基准.因此，评价理所当然地是教学中的重要环节.笔者在教学设计的同时跟进评价，此单元起始课采用单元任务完成表现性评价方式，针对5个任务的要求设计相应的教学评价要求，评价5个任务之下的教学目标达成情况以及学生的素养发展状况.在评价设计中，笔者进一步审视教学目标的适切性、科学性和精准性，从而有效地分解教学目标并设计评价要求，以保证目标与评价的一致性.

（三）建构方法路径，预设教学流程

课堂教学中的“教—学—评”一致性主要围绕学生的学习目标展开［3］.单元教学以“整体统摄，先行组织”为基础，实质内容是“整体策划清脉络、整体建构搭框架、 整体勾勒绘蓝图”［4］.“圆”单元主题为“圆的概念”“圆的性质”“与圆相关的位置关系”“圆的运算”，教师可以按照“知识要点—思想方法—核心素养”的逻辑思想统整单元整体教学结构.其中，“圆的概念”建构的思考方法与路径如图2所示.

基于上述思考，笔者设置了如图3所示的教学流程.

三、问题串联驱动，过程评价伴随，保证实现“教—学—评”一致性的高效实施

要实现单元整体教学的目标，就需要在整体建构的基础上把学习目标分解为一个个学习任务，通过活动设计、问题驱动把学习任务转化成学生核心素养发展的要求.

【任务1】再认大概念“圆”并抽象生成“圆”概念

［活动1］创设情境，激活经验，提出问题

问题1：观察课本封面及第36～37页的4张图片，你会发现怎样的“共同”的几何图形？说说小学里已经探讨过它的哪些内容？

设计意图：欣赏课本图片，感悟几何研究对象——“圆”的广泛存在，引发起对圆的相关知识的回顾，激活原有认知经验.

问题2：战国时期思想家墨子撰写的《墨经》一书中就有“圆，一中同长也”的记载，你理解这句话的意思吗？

（1）视频观察：你发现了圆的哪些要素？圆的位置和大小分别是怎样确定的？

（2）动手操作：在同一平面内将线段OP绕端点旋转一周，你有什么发现？类比角的概念尝试给圆下一个定义，并尝试把圆用数学符号表示.

设计意图：采用“圆，一中同长也”的数学文化情境，激发学生的学习兴趣和对中国历史文化的认同；动手操作，观察发现，用类比的数学思想抽象出圆的动态描述定义，发展几何直观和数学抽象能力.

教学评价：能用数学的眼光审视现实世界，基于实际问题发现圆的要素；能基于数学类比思想，通过类比角的概念，提出圆的概念；能基于抽象能力的发展，通过类比角的平分线（或线段垂直平分线）归纳圆的描述性定义.

【任务2】初步感悟圆的知识结构体系和研究方法

［活动2］类比建构，发展经验，生成结构

问题3：（1）从圆的定义出发，思考圆有怎样的性质和怎样的判定.

（答案：圆上的点到圆心的距离等于半径；到圆心的距离等于半径的点在圆上）

（2）类比角的平分线或线段的垂直平分线的集合定义，尝试给出圆的集合定义.

设计意图：认识圆的概念的两重性（既是性质也是判定），用类比的数学思想抽象出圆的集合定义.

教学评价：能基于抽象能力的发展，进一步揭示圆的概念的本质特征，通过类比角的平分线（或线段垂直平分线）归纳圆的集合定义.

问题4：（1）从对称性的角度考虑，圆的对称性情况是怎样的？从点、线、角、面的角度，思考与圆关联的几何对象，尝试给出一些名称.

（引出：弦、弧、圆心角、圆周角等名称）

（2）操作实践：翻折图形或旋转图形（参照课本第46页图2-13和课本第44页图2-10），说说你对这几个图形有哪些发现.