选择·规划·组织：基于结构化的中考数学复习教学探究

摘    要：当前，中考备考复习阶段的数学教学存在以题代教、零散脱节等问题，导致教学缺乏系统规划，学习缺乏内生发展秩序.为有序高效地进行中考数学复习教学，教师可基于对中考试卷的分析，坚持育人导向进行内容选择，坚持素养导向进行系统规划，坚持目标导向进行教学组织，构建基于结构化的中考数学复习教学样态.具体教学中，教师可基于该样态构建复习体系、厘清知识关联、凸显学生立场，体现精准、系统和整体三大优势，切实增强复习教学的实效性，促进学生对知识内容的结构化理解，进而提升关键能力，发展核心素养.

关键词：结构化；中考数学复习教学；教学样态

2024年是新课改以来浙江省初中学业水平考试全省统一命题的第一年.数学试卷坚持素养立意，凸显育人导向，体现“教—学—评”一致性，发挥了试卷的教学导向功能，特别是对中考备考复习阶段的导引意义深远.通过调研，笔者发现中考备考复习阶段的数学教学（以下简称“中考数学复习教学”）还存在着以下问题：以题代教，教学缺乏系统规划，追求“量的覆盖”而忽视“质的落实”；零散脱节，学习缺乏内生发展秩序，不断“低阶重复”而忽视“思维培养”.通过对新中考的研究和对现状的分析，我们还需进一步思考：如何有序高效地进行中考数学复习教学？如何解决核心素养落实问题？如何着眼于构建数学核心知识体系、着力于形成结构化的学习能力？

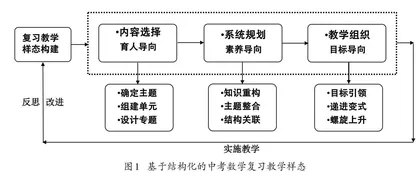
《义务教育数学课程标准（2022年版）》（以下简称“《义教数学课标》”）提出：在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系.所谓“结构化”，是依据逻辑将相关内容进行合理组织，使它们彼此相互关联、产生作用，构成一个有意义的整体.因此，基于结构化实施中考数学复习教学，有助于学生建立系统整体的数学认知，发展核心素养. 在实践中，笔者坚持育人导向进行内容选择，坚持素养导向进行系统规划，坚持目标导向进行教学组织，构建了基于结构化的中考数学复习教学样态（如图1所示），下面具体阐述.

一、内容选择：育人导向，构建复习体系

中考复习时间短而内容庞杂，面面俱到只会导致劳而无功.鉴于中考考查的不同知识、技能、素养等，在卷面分值的配比、难易的程度上都有其不同的“权重”，教师需要在结构化地认识、把握数学知识内容以及学情的基础上，梳理出知识内容所考查的“轻重程度”，并在复习的“着力程度”上加以体现.这表明，复习内容的选择和实施要有导向性和针对性.教师要立足内容的育人价值，从内容的效度、蕴含的思想、承载的素养等维度出发，选择适切的教学内容，引导学生梳理知识、分析要点、厘清层次.

（一）基于课标和学情分析，确定复习主题

【案例1】“代数式”复习主题的效度分析

根据《义教数学课标》对“代数式”内容提出的学业要求，我们可以从五个层次对其内容进行结构化梳理（如表1所示）.

在新课阶段，学生对“代数式”内容已经有了较深认识：对代数式，充分经历了“概念+算理+算法+公式”的学习过程；对代数模型，也从“概念+解答（求解或性质探究）”走向“实际情境+模型构建+模型解答+问题解决”.但在知识结构化梳理的层面，对各类代数式如何基于“运算单元逐步复合”的内在逻辑，大部分学生还不能从知识结构的整体出发加以关联；在关键能力层面，比如基于公式进行运算程序的优化、代数推理，以及基于建模优化的代数应用等，学生也有待提升.因此，中考复习教学中可以突出“运算”和“建模”两个主题，并分别以“公式运用：重新认识代数式+代数式变形及延伸拓展”和“代数表达：模型构建解决问题”为载体，帮助学生进一步梳理知识结构，提升关键能力.

分析：《义教数学课标》中的相关要求和学情分析是衡量复习内容效度的标尺.只有对知识内容的课标要求建立整体的、结构化的认知，才能明晰考查的知识内容及程度，从而有效确定教学的目标和重点.同时，要对学情有充分的认识，分析现状与目标之间的差距，从而有效确定教学的起点和难点.因此，复习主题的确定要以《义教数学课标》和学情为依据，如此才能提升复习教学的效度.

（二）聚焦关键能力提升，组建复习单元

【案例2】“代数推理能力”复习单元

代数推理在形式上主要表现为代数结构的转化变形，其本质是运算律和等式（不等式）性质的灵活运用.在新课阶段，学生已经有了一定的代数式运算、因式分解等代数式结构恒等变形的经验，同时也具备了一定的简单方程（组）、不等式（组）等关系式等价变形的经验.因此，在中考复习阶段，教师需要帮助学生进一步明确代数式结构变形的思维方向，将抽象的代数推理变得“具象化”“可视化”.笔者以乘法公式及其组成要素的关系研究为线索构建复习单元，引导学生达成五个方面的理解，提升代数推理能力.“乘法公式”复习内容结构化梳理如表2所示.

分析：在课堂上要立足学情，帮助学生在学习过程中进一步提升数学关键能力，教师需要做到如下几点：（1）梳理核心素养的表现要求和学生已经具备的能力；（2）清晰了解现状与目标之间的差距；（3）选择合适的单元内容作为载体，帮助学生提升关键能力.

（三）借助历年真题研究，设计复习专题

【案例3】二次函数的“单调性、最值”“零点问题”复习专题

历年中考真题中，多次以二次函数的“单调性、最值”“零点问题”为背景，举例如下.

［2024年浙江省中考数学第23题第（3）小题］ 已知二次函数y=x2+bx+c（b，c为常数）的图象经过点A（[-]2，5），对称轴为直线x=[-12].当[-]2≤x≤n时，二次函数y=x2+bx+c的最大值与最小值的差为[94]，求n的取值范围.

［2022年杭州市中考数学第22题第（3）小题］设二次函数y1=2x2+bx+c（b，c是常数）的图象与x轴交于A，B两点.设一次函数y2=x-m（m是常数），若函数[y1]的表达式还可以写成y1=2（x-m）（x-m-2）的形式，当函数y=y1-y2的图象经过点（x0，0）时，求x0-m的值．

分析：这两个问题属于“函数观念”的考查，涉及二次函数中“对称轴”“单调性、最值”及“两个二次（二次函数和一元二次方程）”等知识，其背景、内容、方法均是函数复习时的重点.笔者将其分别作为二次函数复习单元中的两个“应用专题”，即“单调性、最值”及“零点问题”，并组织教学加以突破.由于一些重要内容在历年的中考卷中会高频出现，教师应对历年的中考真题有比较深入的研究和把握，并在此基础上设计适切的教学内容，然后以专题的形式带领学生学习、探究，使其更深入地理解问题的本质、掌握解决问题的方法，发挥专题教学最大的价值.

二、系统规划：素养导向，厘清知识关联

在新课学习和单元复习阶段，学生已在教师的引导和帮助下，初步梳理和构建了单元内知识之间的联系和结构；而在中考复习阶段，教师在已选复习内容的基础上，还需进一步梳理知识内容之间的关联，形成结构化的内容单元，帮助学生形成整体的数学认知，提升数学核心素养.

（一）知识重构，体现知识构建的系统性

【案例4】代数式的“概念和规则”重构

在新课阶段，由于学生缺乏认知经验，教师在教学时通常从生活实际引入，并将其抽象得到各类代数式的概念，再进一步通过归纳得到其运算的规则.而在中考复习阶段，教师则可以引导学生在原先研究的基础之上，从主题内跨单元知识之间的逻辑联系出发，对知识进行重构.如“代数式”复习，教师可引导学生类比数系扩充的过程，以整式六则运算结果的封闭性研究为线索，对代数式的扩充过程及内在逻辑进行再探，其结构化梳理如图2所示.

分析：经历这样的认知重构，有助于学生重新认识分式、二次根式的代数结构.让学生进一步理解分式、二次根式的运算规则构建的底层逻辑，即化归为整式运算，如二次根式[a]，[b]的乘法运算法则是[a]×[b]=[a×b（a≥0]，[b≥0）]，将根式的乘法运算化归为根号下的整式乘法运算，可帮助学生整体把握和梳理知识结构，提升抽象、运算和推理能力.

（二）主题整合，实现知识学习的连贯性

【案例5】“代数模型”的主题整合

在新课阶段，“代数模型”内容缺乏主题化整合的条件，如各类方程的学习要以相应的代数式的学习为基础，故以螺旋上升的方式呈现.到了中考复习阶段，则可以基于知识发展的阶段性关联进行主题间的整合：通过真实问题情境的创设，引导学生分析问题所描述的数量关系或变化规律，构建合适的“代数模型”解决问题，并比较不同“代数模型”之间的优劣，梳理它们之间的联系和结构.

目标：以代数应用题为载体，提出不同层面的问题（导向构建代数式、方程、不等式、函数模型解决），发展学生的抽象能力、推理能力、模型观念（应用意识、创新意识）.

内容：以用“代数式”描述现实问题或数学问题中的量为基础：（1）通过“运算”解决问题；（2）构造“方程与不等式”解决问题（数量关系：相等关系和不等关系）；（3）构造“函数”解决问题（变化规律）；（4）梳理函数、方程、不等式之间的差异和联系；（5）解决函数视角下的方程、不等式问题.

分析：代数是用数学的语言表达现实世界的一种方式，基于真实的问题情境构建合适的“代数模型”是用数学的方式解决问题和表达观点的有力工具.通过对不同代数模型的主题式整合，可以明晰它们各自的特点和应用的场景，而梳理它们之间的差异和联系，则能够在不同的场景下构建合适的模型解决问题、解释问题，并在这一过程中发展抽象能力、推理能力、模型观念（应用意识、创新意识）.

（三）结构关联，揭示知识内在的本质性

【案例6】因式分解（降幂思想）统合“两个二次”

“降幂化归”是一元二次方程解法构建的底层逻辑：“直接开平方法”“配方法”“公式法”均通过“开方运算”达成“降幂化归”为一元一次方程的目的.“公式法”是解一元二次方程的通法，但其“解法构建”的过程无法推广到“解更高次方程”当中，而通过“因式分解”“乘法法则”达成“降幂化归”所构建的“因式分解法”则可向“更高次”推广.“因式分解”过程中所形成的恒等关系式ax2+bx+c=a（x-x1）（x-x2），是进一步探索“根与系数的关系”，以及利用二次函数交点式解决“零点问题”的逻辑起点，由此可以构建“两个二次”之间的关联结构.

分析：在涉及“两个二次”问题的解决中，利用“因式分解”将函数表达式转化为交点式是关键，但学生不易想到.因此，新课阶段需要帮助学生在能够利用“公式法”解一元二次方程的基础上，建立起其与“因式分解法”之间的关联，渗透降幂思想，而在中考复习阶段，则应当帮助学生梳理“两个二次”之间的关联，加强“二次函数统领下的二次方程”的教学，使其明晰“因式分解”在二次函数“零点问题”中所起的作用，从而揭示数学本质.

三、教学组织：目标导向，凸显学生立场

在课堂上，教师要建立一种在整体把握知识内容、全面认识素养表现、充分理解学情的基础之上开展复习的理念.结构化的中考复习教学，正是基于这种理念，在合理的内容选择和系统的单元规划之下进行的.

（一）目标引领，开展“主题+单元+专题”的组织形式

【案例7】“代数式变形及延伸拓展”主题复习

主题：代数式变形及延伸拓展.

目标：发展学生的运算能力和推理能力.

内容：以乘法公式及其组成要素的关系研究为线索，构建学习单元（如表3所示）.（注：每一单元根据不同的情境和任务“容量”设置1～2个专题.考虑到学生运算和推理能力有了提升，在知识结构化的前提下，适当地增加了范围和难度）

分析：整式、分式、二次根式的单元之间存在着联系：分式、二次根式是整式除法（不能整除）、开平方（开不尽方）运算的结果，其变形和运算可以转化为分子（分母）、根号下的整式运算，因此单元2和单元3是单元1的自然延拓.此外，单元内的不同应用场景之间内容涵盖全面，存在关联且逐层递进.因此，在教学目标的引领下，主题式的内容呈现应在组织形式上体现内容之间的关联和结构.