基于结构化的“单元—课时”教学设计

摘    要：“单元一课时”教学设计通过分析“主题—单元—课时”的数学知识和核心素养联系，促进学生对学习内容的整体理解与把握.这要求教师整合主题，体现内容的结构化.具体教学中，教师可解析单元内容、目标，基于教学问题诊断及教学支持条件分析，制订课时目标，明确教学重难点，按照“提出问题—获得概念—研究性质—尝试应用—概括总结”的流程实施教学，注重情境创设，突出探究过程，深化研究路径，发展学生空间观念、几何直观和推理能力，逐步培育学生的核心素养.

关键词：结构化；“单元—课时”教学设计；图形的变化

《义务教育数学课程标准（2022年版）》（以下简称“《课程标准》”）在“教学建议”中指出，要改变过于注重以课时为单位的教学设计，推进单元整体教学设计，体现数学知识之间的内在逻辑关系，以及学习内容与核心素养表现的关联.这充分体现了数学是研究数量关系和空间形式的科学，具有知识内容结构性的基本特征.“单元—课时”教学设计是在单元教学设计的基础上，再给出课时教学设计，可充分体现教学的整体性、逻辑的连贯性、思想的一致性、方法的普适性和思维的系统性［1］ .它通过分析“主题—单元—课时”的数学知识和核心素养联系，促进学生对数学教学内容的整体理解与把握，使其可用相同（相似）的方法解决不同的问题，逐步提升核心素养.

“图形的旋转”是浙教版义务教育教科书《数学》（以下简称“浙教版教材”）九年级上册第三章《圆的基本性质》中的内容，位于图形的平移、轴对称和中心对称等内容之后.这些内容都属于“图形的变化”，却分散在各个年级与章节，极易导致知识的碎片化.那么，我们要如何通过主题整合的方式，从整体与结构上认识这些知识之间的关系，体现内容结构化呢？下面，笔者设计“图形的变化”单元，以第4课时“图形的旋转”为中心课时，探讨基于结构化的“单元—课时”教学设计，引导学生理解数学本质、感受数学思想方法，从而站在更高位上认识数学教学活动［2］.

一、单元内容、目标及解析

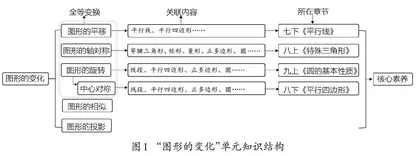
“图形的变化”包含图形的平移、图形的轴对称、图形的旋转（其特殊化是中心对称）三类基本的图形运动，以及图形的相似、图形的投影等内容. 三类基本的图形运动属于全等变换，都是通过实例抽象并概括相关概念，要求学生理解其基本特征，探究图形的变化规律和变化中的不变量，为进一步学习“图形与坐标”，用代数方法表达图形特征，发展数形结合思想奠定基础.

（一）单元内容及解析

“图形的变化”单元知识结构如图1所示.

“图形的变化”强调从运动变化的观点来研究图形的基本性质和相互关系，理解图形变化时的变化规律和变化中的不变量，系统掌握图形变化学习的方法，形成图形变化学习的一般观念.

该单元可采用“实物观察—归纳猜想—演绎证明”的流程进行教学，借助起始课“图形的平移”的研究思路、方法与路径，引导学生通过类比来研究图形的轴对称、旋转和相似.这一研究蕴含着图形运动变换、抽象、推理等思想方法，具有发展学生空间观念、几何直观、抽象能力、推理能力、数学审美能力等育人价值.

图形的变化源于现实世界中的物体及其运动、变化，是对物体运动、变化的数学抽象，由此可确定该单元的教学重点：在对同一类物体运动特征的观察中产生研究对象，并用推理的方法研究图形变化的概念与性质，形成研究图形变化的一般观念.

（二）单元目标及解析

根据以上分析，笔者设计了三个单元目标.

单元目标1：通过“操作猜想、实验验证、推理证明”等活动，经历图形变化各个概念的形成过程，体会相关概念获得的一般方法.

单元目标2：探索并归纳图形变化的性质，知道运动过程中的不变量、图形运动的变化特征，会按要求作出简单平面图形变化后的图形.

单元目标3：能用图形的运动认识、理解和表达现实世界中相应的现象，能用图形变化的性质解决简单几何问题，发展几何直观、空间观念和推理能力.

然后，笔者对三个单元目标的达成情况作了解析.

达成单元目标1的标志：经历实物观察、操作实验、想象归纳的过程后，学生知道平移、轴对称、旋转等图形变化的特点，能从相关要素角度抽象、表述概念.如“图形的旋转”是利用“旋转中心、旋转方向和旋转角度”三个要素来描述概念.

达成单元目标2的标志：学生能从边、角的数量关系以及图形的位置关系等角度，对比变化前后的两个图形，猜想、验证并得出变化规律“图形中任意两点间的距离保持不变，夹角也保持不变”，并能够证明其性质.

达成单元目标3的标志：学生能理解图形变化的概念、性质，按要求作出简单平面图形变化后的图形，并能设计图案.

二、教学问题诊断及教学支持条件分析

小学阶段学习图形变化的有关知识和方法，侧重于感性认识，而初中学习“图形的变化”，则侧重于对其性质的探索和理解，要求运用其性质进行简单图形变化的作图.在图形变化中，轴对称、平移、旋转均属于保距变换，和全等图形的关系比较密切；相似则是保角变换.要得出这些相关性质，学生往往需要经历复杂的探索过程，仅通过推理是很难完成的，此外，在运用实际操作和作图两种方法来解决有关图形变化的问题时，涉及的要素比较多.由于学生尚未掌握几何学习方法，尚未构建出学习思路，这些就构成了该单元学习的难点.

因此在教学时，教师应尽可能地选择学生熟悉的生活实例创设情境，通过信息技术的演示或者实物的操作，让学生感悟图形变化的特征，帮助学生理解几何学的本质.

三、课时教学设计

在实施单元整体教学时，教师需要思考“单元呈现”和“课时表达”的“总—分—总”路径，使学生经历前后一致、逻辑连贯的完整学习.从图1我们可看出，浙教版教材对三类基本图形运动的学习安排，是分散在四册书中，其中“图形的旋转”是笔者所设计单元的第4课时，它是学生学习了平移、轴对称后的又一种图形的变化方式.

（一）课时目标

根据《课程标准》中的相关要求以及学情，笔者设置了如下三个课时目标.

（1）了解现实生活中的图形旋转，通过“实验观察、抽象本质、验证辨析”，经历旋转概念的形成过程，进一步体会图形变化相关概念获得的一般方法.

（2）会按要求作出简单平面图形旋转后的图形，能用旋转的性质解决简单几何问题.

（3）发展实物操作中的直观想象能力，以及观察、归纳、论证过程中的逻辑推理能力等.

（二）教学重点难点

重点：图形旋转的概念和性质.

难点：性质“对应点与旋转中心连线所成的角度等于旋转角”的发现；图形旋转的作图设计涉及要素较多.

（三）教学设计

1.提出问题

问题：关于图形变化，我们已经学过哪些内容？如何得到相关概念？（展示图形旋转的相关图片）接下来，我们要学习的新的图形变化是什么？你还能举出其他实例吗？

［师生活动］引导学生回顾“图形的平移”“图形的轴对称”等概念的获得过程，完成数学抽象；根据学生列举的旋转实例，提出新的研究内容.

追问：类比图形平移、轴对称的研究，你认为可按照怎样的路径从哪些角度研究图形的旋转？

［师生活动］类比图形平移的研究路径，引导学生尝试从旋转实例中发现变化过程中的特点，规划图形旋转的研究思路.

设计意图：引导学生联系图形的平移、轴对称和旋转，认识其特征，形成推理意识，体会旋转是图形变化中的一类，有继续研究的必要性，进而提出研究问题，规划研究路径.

2.获得概念

问题：类比“图形的平移”和“图形的轴对称”概念的获得过程，你将如何得到图形旋转的概念？可从哪些角度表述这一概念？

［师生活动］引导学生观察旋转图形，如风车叶片、钟表指针的转动过程，概括旋转的共同特点，由此获得“图形的旋转”概念.

追问1：图形平移的要素是方向和距离，那么图形旋转的要素是什么？尝试在图形（图略）上标注出来.

［师生活动］选择一个图形的实物，在实例中找旋转中心、旋转方向、旋转角度等旋转的要素，进一步感受问题的本质.

设计意图：观察现实生活中物体旋转的实例，通过追问引导学生对旋转本质特征进行抽象和概括，类比“图形的平移”概念，尝试归纳旋转的共同特征并给出定义，体会旋转的条件，促进对旋转本质的理解，发展抽象能力、直观想象.

追问2：对于一双手的图片，经过轴对称，能否使得左手图与右手图重合？经过旋转可以做到吗？

［师生活动］联系图形轴对称的判定方法，即寻找关键点来判定图形旋转，然后通过旋转的三个要素画出旋转的图形.

设计意图：用正例与反例，根据概念中的关键词，通过操作或寻找关键点，来判断两图之间的运动是不是旋转.这为得出旋转的性质打下基础，发展学生的推理能力.

3.研究性质

问题：图形的平移是从平移的方向、距离等要素概括其性质，你将如何研究图形旋转的性质？从哪些角度概括其性质？

［师生活动］类比图形的平移，形成研究图形旋转的路径：画图探究—联系概念（旋转角度、中心和方向）—观察发现（要素的变与不变）.一是画出图形提炼画法，通过作出△ABC按逆时针旋转80°后的图形，形成旋转图形作图的一般方法：寻找图形的关键点，通过“找到旋转中心和旋转方向，用量角器确定旋转角”作出对应点.二是联系概念概括性质，通过△ABC内任意点P的探究，得出性质：（1）对应点到旋转中心距离相等；（2）任何一对对应点与旋转中心连线所成的角度都等于旋转角.

设计意图：类比平移作图方法，联系旋转概念，有序作图，从而有效突破作图的难点.对旋转概念中减少要素的探究，旨在促进学生对问题本质的理解，形成严密的推理思维.引导学生经历“操作、观察、猜想、验证”的研究过程，得出图形运动的一般概念，即体会运动前后图形的变与不变，通过类比、猜想、发现结论，并利用概念定义进行简单的推理，获得并理解旋转的性质.

追问：图形的旋转有特殊情况吗？尝试画出一个图形.

［师生活动］当旋转角度为180°时，原图形与旋转后的图形关于点O成中心对称.

设计意图：特殊化的研究，使旋转与中心对称图形产生关联，丰富了图形旋转的内涵.

4.尝试应用

问题：如图2，已知矩形AB′C′D′是矩形ABCD以点A为旋转中心，按逆时针方向旋转90°所得的图形.求证：BD⊥B′D′.

思考：（1）证明两条直线互相垂直，有哪些经验？（2）如果选择证明∠ABD+∠B′D′A=90°，是基于哪三点共线的前提？你将如何说明？（3）联系旋转的概念、性质，有没有与∠ABD相等的角？有没有与∠B′D′A相等的角？

［师生活动］先通过矩形性质和旋转90°的条件，证明D′，A，B三点共线，再联系旋转的性质，证明BD⊥B′D′.

设计意图：用图形旋转的性质解决问题，学习分析证明思路的方法，发展几何直观以及推理能力.

5.概括总结

问题：通过这节课的学习，你获得了哪些新知？按照怎样的路径研究？进一步将学习什么？

［师生活动］引导学生通过小结，概括出知识结构图（如图3所示）.

四、教学建议

（一）注重情境创设

图形的变化源于现实世界中的物体及其运动、变化，是对物体运动、变化的数学抽象.教学时应尽可能地从学生熟悉的方面创设情境，并力求丰富多彩.如选择学生所熟悉的风车、闹钟等图片来创设情境，一方面能充分利用学生的生活经验，唤起学生的想象，体现《课程标准》中的“通过具体实例认识”图形变化的要求，另一方面能体现数学与生活的联系，有利于激发学生的学习兴趣，让学生主动投入到学习活动中来.

（二）突出探究过程

《课程标准》对“图形变化的性质”的教学要求是，运用实例，通过画图使学生直观地感受到其“变”与“不变”，发展核心素养.同时，由于图形的变化源于物体的运动，是对物体运动的数学抽象，并与相关图形密切相关，如平移与平行线，轴对称图形、图形的轴对称与等腰三角形，旋转、中心对称与圆、平行四边形等.因此，可通过平移引出图形变化的一般概念，通过图形的轴对称发现并掌握等腰三角形的性质，通过旋转理解平行四边形的性质与判定，借助圆旋转的不变性探索圆中弧、弦、弦心距、圆心角之间的关系.教师应通过活动，让学生经历操作和思考，去发现这些关联，在形成、验证命题的过程中深刻理解性质.就“图形的变化”单元而言，可借助几何画板的可视化功能帮助探究.

（三）深化研究路径

“图形的变化”单元的主要研究对象是图形的变化.图形的轴对称、平移、旋转和相似之间存在内在联系，其研究的程序、途径、依据、结果、表达等构成方法体系.内容结构化即通过核心概念使零散的内容建立起联系，可促进知识与方法的迁移，及核心素养的形成.如在“图形的平移”学习中形成的研究路径，在“图形的旋转”学习中就可以应用，并进行深化（“图形的变化”研究路径如图4所示）.用图文并重的形式，把学生的注意力集中在关键词及其内在联系上，可使其产生清晰的联想，形成推理的路径，提升思维深度.而通过类比，形成研究几何图形的一般观念，以此为统领进行前后连贯、逻辑一致的教学，可帮助学生构建有序、系统的知识结构.

参考文献：

［1］章建跃.《普通高中教科书·数学（人教A版）》“单元—课时教学设计”体例与要求［J］.中学数学教学参考，2019（22）：14-16.

［2］方长林.聚焦数学核心素养    设计单元—课时教学——以高中“一元二次函数、方程和不等式”单元为例［J］.数学通报，2021（6）：30-35.