基于层次分析-模糊综合评价的线上课程质量评价研究

摘  要：随着“互联网+”时代的到来，纯线上教学和线上-线下混合式教学已成为高等教育教学模式发展的新趋势，也是近年高等教育教学改革研究的热点。为淘汰“水课”，国家大力打造线上“金课”，期望起到标杆和导向作用。如何对线上课程教学质量进行全面、科学的评价则直接关系着提升线上课程质量、甄别线上课程含金量以及更好地发挥金课的“标杆”作用。该文以学生为中心，突出学生评价主体地位，考虑目前我国主流慕课平台的发展现状以及线上课程教学特点和规律，采用AHP层次分析法构建一套较全面、合理的线上课程质量评价指标体系，同时结合模糊综合评价法对线上课程质量进行量化评估。其成果可为高校或者广大教师进行线上课程质量评价提供理论支撑和指导建议。

关键词：互联网+；线上课程；课程评价；层次分析法；模糊综合评价法

中图分类号：G642        文献标志码：A          文章编号：2096-000X（2024）02-0096-06

Abstract： With the rapid development of IT technology， pure online teaching and online-offline hybrid teaching have become a significant trend of teaching mode in higher education and a hot spot in the field of higher-education teaching reform in recent years. In order to improve the course quality， the ministry of education is carrying out a "National Level First Class Courses" program to launch a number of "Gold Courses" with excellent quality and high standard. An evaluation system of teaching quality of online courses plays a crucial role in promoting the quality of online courses and helping teachers to reflect. It is worth exploring how to construct a comprehensive and scientific evaluation system of online courses. In the paper， considering the characteristics of online teaching and development status of mainstream MOOC platforms in China， the Analytic Hierarchy Process （AHP） method is applied to design an evaluation factor system which is student-centered and takes students as dominant position of evaluation. Moreover， combining with the fuzzy comprehensive evaluation （FCE） method， the quality of online courses is quantitatively evaluated. The research can provide the theoretical support and guidance for teachers to evaluate quality of online courses.

Keywords： Internet plus; online course; course evaluation; analytic hierarchy process; fuzzy comprehensive evaluation

随着“互联网+”时代的到来，纯线上教学和线上-线下混合式教学等已成为高等教育教学模式发展的一个新趋势，也是近年高等教育教学改革研究的热点。自2019年12月新冠感染疫情爆发以来，国内各高校采取多种形式的线上教学，以保证教学正常展开。据教育部统计，2020年度全国高校采取在线教学形式的课程开出率达到91%。由此可见，这次疫情爆发极大推动了在线教学在我国高等教育领域内的推广和发展。

线上教学打破了传统课堂教学在时间和空间的限制，为学生提供了一种更便捷、灵活、开放的学习方式[1-2]。其发挥了学生学习的自主性，但同时也要求学生具有一定的学习自律性。另一方面，线上教学在很大程度上也有效缓解了课堂教学学时不足的问题。但是，近年通过大量的线上教学实践，线上教学也暴露出一系列突出的问题，例如教师较难对学生的学习进行督促，学生线上学习的完成率不高，课程优秀率和通过率较低，线上课程教学质量的评价体系还不够完善和科学等。

由于传统课堂教学与线上教学有很多显著的差异，因此传统课堂教学的质量评价体系并不适用于线上课程的教学质量评价。各高校应该充分考虑线上教学的自身特性以及我国线上课程的发展现状，来构建合理的线上课程教学质量评价体系。此外，线上课程教学质量评价体系在具体实施过程中涉及到不同学科特点和课程性质等诸多因素，需要制订全面的且科学的评价体系。

近年来，国家级和省级线上一流课程作为高品质的“金课”的出现，受到高校教学管理者和广大高校教师的重视，也吸引了众多大学生的关注。为了更好地发挥金课的“标杆”作用以及提升线上课程含金量，迫切需要解决好线上课程质量评价的问题。因此，本课题针对线上课程，期望基于AHP-模糊综合评价模型构建一套科学合理的线上课程质量评价体系，以此来监督并改进线上课程的质量，提升线上课程的含金量。本项目成果可为各高校以及各高校教师构建线上教学课程评价体系提供理论支撑和指导。

一  线上课程质量评价组成要素分析

经过近十年的发展，我国已经孕育出一批较知名的慕课平台，例如爱课程（中国大学MOOC）、学堂在线、智慧树网、学银在线等。目前，这些较知名慕课平台的硬件和技术水平均能够较好满足线上课程的教学活动需求。特别是新冠感染疫情期间，由于在线访问量剧增，众多慕课平台均增大了对硬件设备的投入，提升了硬件性能和规模。此外，经过多年的发展，我国各大慕课平台均具备强大的技术支持，提供完善的教学和学习功能以及拥有人性化的界面设计。各慕课平台所提供的各种学习活动操作和教学活动操作均简易且较人性化，在线学习体验都较好。各平台所提供的教学功能差异性不大，学习体验均较令人满意。因此，结合目前我国慕课网站平台的发展现状，考虑到以上因素，本文在构建线上课程质量评价体系时，一些与线上课程的软、硬件支持和在线学习体验等有关指标，具体包括课程视频能否打开并且流畅播放、课程的导航系统设计是否直观明确、教学和学习功能是否完善、各种操作的简便易用性、是否能追踪记录每个学生的整个学习过程以及提供课程数据的分析、慕课平台的兼容性等，将不再作为评价指标。本文将从教学资源、教学设计、教学支持、教学评价四个维度，围绕“学生为中心”，突出学生主体地位，来构建线上课程质量评价体系。

二  基于层次分析法构建线上课程质量的评价指标体系

（一）  层次分析法简介

层次分析法（Analytic Hierarchy Process，AHP）是美国运筹学家T. L. Saaty等在20世纪70年代提出的一种定性和定量分析相结合的多准则决策方法[3-4]。通过构建层次模型，可以利用较少的定量信息将决策的思维过程数学化，非常适合于对决策结果难以直接计量的场合。

层次分析法（AHP）把一个复杂的多目标决策问题视为一个整体，将总目标分解成为多个子目标或准则，再进一步分解成为多指标或多准则、多约束的若干个层次，从而分解为有序的递阶层次结构，即层次结构模型。通过将定性的指标进行模糊量化的方法来计算出各个层次的单排序（权重数）和总排序，从而对多目标、多指标的多方案进行优化决策[3-5]。

（二）  线上课程质量评价指标体系的设计

本文运用层次分析法（AHP），构建线上课程教学质量评价体系。该线上课程教学质量评价体系包含教学资源、教学设计、教学支持和教学评价共4个一级评价指标和19个二级评价指标，具体见表1。

（三）  建立判断矩阵

在AHP方法中，构造两两比较判断矩阵是较关键的一个步骤。根据所建立的具有层次关系的线上课程质量评价体系（表1），针对各层次中处于同一级别的任意两个评价指标，进行重要程度的比较并进行定量化的判断（表2），从而可构造出面向不同层级的两两比较的n×n判断矩阵A（aij）n×n。

表2中，Ai（i=1，2，3，…，n）是处于同一层级的评价指标，判断矩阵中的元素aij（i，j=1，2，3，…，n）代表评价指标Ai与评价指标Aj的重要程度的比较。对判断矩阵中的元素aij的赋值，则需要对同一层级任意两指标的相对重要程度比较判定进行定量化。常采用的方法是用数字1～9及其倒数来对任意两要素相对重要程度比较来进行标度，标度值及其含义见表3。

判断矩阵A具有如下两个特性：

本项目邀请8位熟悉线上教学的专家和6位具有丰富线上教学经验的中青年教师对处于同一层次的所有评价指标的重要程度进行两两比较，根据表3给定的定量赋值标准进行赋值，构建不同层级的判断矩阵，即1个A-B层级的判断矩阵和4个不同B-C层级的判断矩阵。

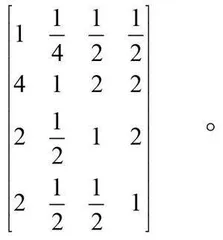
本文以A-B层级为例，教学专家和教师给出的判断矩阵为

（四）  计算各指标的相对权重并对判断矩阵进行一致性检验

首先计算判断矩阵A的最大特征值λmax及其对应的特征向量W，即

AW=λmaxW。

归一化的W向量各元素为相对应评价指标的相对权重值，即该因素相对于上一层级对应因素的相对重要性的权重值。

随后，通过计算一致性指标CI（Consistency Index，CI）来对判断矩阵Ａ进行一致性检验。一致性指标CI的表达式为

式中：n为判断矩阵Ａ的阶数。若一致性指标CI=0，则表明该判断矩阵Ａ具有完全一致性；若一致性指标CI≠0，则需要进行随机一致性比例CR（Consistency Ratio，CR）的计算，继续检验判断矩阵的一致性。

一致性比例CR的表达式为

式中：RI为平均随机一致性修正系数（Random Index，RI），其值可通过查表获得。表4列出了判断矩阵的不同阶数n所对应的修正系数RI值。根据判断矩阵的阶数n，可查找相对应的平均随机一致性修正系数RI。

若一致性比例CR＜0.1，则可认为判断矩阵通过一致性的基本检验；若一致性比例CR>0.1，则认为判断矩阵没有通过一致性检验，需要对判断矩阵进行调整和修正，直至通过一致性检验。只有通过一致性检验后，归一化的W向量各元素才能作为权重值。

本文以A-B层级为例，求其判断矩阵的最大特征值λmax和相对应的归一化特征向量WB，得到λmax=4.060 6，WB=[0.109 7，0.438 4，0.265 2，0.186 6]。

随后对A-B层级的判断矩阵进行一致性的基本检验。一致性指标CI

通过查询平均随机一致性修正系数对照表（表4），得到当n=4时，一致性修正系数RI=0.89。将其代入下式，计算一致性比例CR。

一致性比例CR值小于0.1，表明该判断矩阵通过了一致性检验，可以将计算得到的特征值和权重作为判断的依据。