高等数学的情境探究式教学设计

摘  要：学生的学习动机大部分源自于运用所学知识解决问题的快感和成就，针对高等数学学习中学生“不知所出，不知所用”，缺乏兴趣和动力等困境，提出情境探究式教学设计。该文阐述情境探究式教学理念、目标和设计原则，探讨基本教学活动的展开策略，包括两个情境（产生数学问题的情境和产生概念或方法的情境）+两个数学化过程（学习活动/画龙）+评价支持+教师抽象（点睛）+应用拓展，以全面提升数学核心素养，为终身学习奠基。

关键词：情境；探究活动；核心素养；高等数学；教学设计

中图分类号：G642      文献标志码：A          文章编号：2096-000X（2024）18-0128-04

Abstract： Most of the students' learning motivation comes from the pleasure and achievement of using the knowledge they have learned to solve problems. Aiming at the dilemma of "not knowing what to do， not knowing what to use"， lack of interest and motivation and so on， puts forward the situational inquiry teaching design. This paper expounds the concept of situational inquiry teaching， objectives and design principles， and discusses the development strategy of basic teaching activities. It includes two situations （the situation of generating mathematical problems and the situation of generating concepts or methods） + two mathematicization processes （learning activities/drawing dragons） + evaluation support + teacher abstraction （the key point） + application expansion， in order to comprehensively improve the core quality of mathematics， laying the foundation for lifelong learning.

Keywords： context; inquiry activities; core literacy; Advanced mathematics; teaching design

学生学习高等数学的困难在于数学知识与其生活相距较远，学生对学习的概念和定理“不知所出，不知所用”，缺乏兴趣和动力，一旦遇到困难时很容易放弃，难以为后续的课程学习奠定知识基础，更与数学核心素养的培养目标相差甚远。学生普遍反映“学了知识不会用”“遇到新问题没思路”，其原因就在于很多时候，教师隐去了太多的为什么，为什么这么说？为什么这样做？怎么会想到这么做？等等。我们的教学无论是内容、方式、评价，还是学习习惯，都侧重于知识的传授和掌握，而轻思维经验的积累。要破解这一难题，需要从两个方面着手：一是创设问题情境激发兴趣，让学生知道知识是怎么来的，学会如何应用；二是引导探究精准支持，精准支持让学生建立信心，创设研究情境让学生学会“做数学”，提高数学素养为终身发展奠定基础。

数学思维发展的“触发器”是问题，所以要破解这一难题，我们认为：最根本的转变就在于以问题为中心，通过创设问题情境，经历发现、构想、归纳和抉择的探究过程，获得创造性解决问题的鲜活体验，发展高级认知和思维。本研究主要针对情境探究式教学模式，从教学理念与目标、教学原则及教学结构和活动程序三个方面，来具体阐述如何设计情境探究式课堂的一些思考和经验，以期对同仁有所启发，使其受益。

一  教学理念与目标

著名数学教育家弗赖登塔尔强调：学习数学的唯一正确的方法是实行“再创造”，也就是由学生本人把要学的东西自己去发现或创造出来；探究性学习正是“再创造”学习方式的最佳途径。数学源于现实，也必须寓于现实、用于现实。数学学习应当从与学生生活体验密切相关的问题开始，发现数学问题，产生数学概念和解决实际问题的数学方法。建构主义认为，数学学习不是一个被动的接受过程，而是一个以已有的知识和经验为基础的主动建构的过程。

情境探究式是将数学教学置于实际或临近实际的情境（问题情境、探究情境、应用情境）中，引导学生借助于情境中的各种信息去发现问题、形成问题，并重组知识和经验产生解决问题的方法，再进一步一般化（数学化）为新的概念或方法，是教师指导下学生主动参与的可定义、可自主、可交互的研讨探究过程。藉此让学生在有意义的问题解决情境中创造知识和应用知识，在探究活动的基础上构建起对数学知识的理解和有关的方法、技能，学会数学学习或将学科解题技巧应用到实际生活的问题中。

这种教学的用意在于因材施教深挖学生潜质，改变知识传输路径，凸显学生学习的自主性。让学生经历数学的“再创造”与“再发现”，并将学到的知识加以综合应用于实践的过程，增强研究和运用数学的兴趣与体验；减少学生的困惑，提高学习效率，减轻学生的负担；体会数学的思想与方法，提高其严谨的逻辑推理能力、熟练的运算能力，以及精准的数量思维、基本建模能力、创新应用意识等数学素养要求，同时持续培养其自主学习能力。

二  教学原则

教学活动需要着重思考具体教学情境与具体数学核心素养培养之间的相关性，因为数学核心素养是学生在具有情境的数学活动中切实感悟、综合理解、反复强化逐渐形成的，主要来源是数学活动经验的积累。课堂活动设计遵循的原则如下。

（一）  主动参与原则

探究性学习重在学习的过程、思维方法的学习、思维水平的提高。学生只有亲历数学事实的过程，才能提出自己的见解，对所学知识有所选择、判断、解释及运用，从而有所发现和创新。

（二）  难度适中原则

提出的问题要接近学生的最近发展水平和能力，抓住知识中最关键、最本质的东西，选择最适合学生的起点，用最直接和最亲近的方式激发学生的学习，这样才能够引起学生思考、探索，使学生都能积极参与到研究中。

（三）  合作交流原则

探究性学习的组织形式是独立学习与合作学习相结合。学习是社会建构的过程，基于情境的探索式学习需要小组的协作，学生通过与他人的协作向自己的思想、信念、感觉和现有的知识质疑，可以在参照他人的过程中来完善自己，从而促进自身的认知发展，所以教学组织以小组合作为基本形式，而智慧教室为小组合作学习提供了便利和保障。

（四）  实践运用原则

尽可能设计一些不同层次的活动让学生全体参与，让每个学生都能开展探究，学会在做中学。

三  教学结构及活动程序

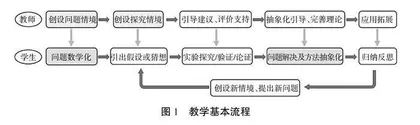
在情境探究式教学的小组合作学习中，创设一种恰当的、内容丰富的情境，建立一套利于学生自主学习和相互协作主动建构知识结构的组织程序是至关重要的。所以教学设计主要依据教学目标和学情分析，围绕两个情境，即产生数学问题的情境和产生概念（或方法）的情境；两个数学化（学生学习活动），即学生形成数学问题（数学关系），也就是问题中关系的数学化和问题解决方法的抽象（新解析关系）数学化展开。基本的教学活动包括两个情境+两个数学化过程（学习活动/画龙）+评价支持+教师抽象（点睛）+应用拓展。

基本流程为：教师创建接近学生生活环境的数学问题情境，引导学生发现问题，形成数学问题（数学关系），即问题关系的数学化，并引起认识冲突，以趣激奇，激发学生解决问题的兴趣。而后在教师创设的问题探究情境（环境和氛围，资源和结构）下，以疑激思，激发学生的探究欲望，师生作为学习共同体，重构已有数学知识，提出解决的方法，进行探究/验证/论证，产生新的概念/对象，把解决的经验总结提升形成明确的表述（经验显化），并进一步一般化抽象化（数学化）（学生画龙），形成数学概念/定理/方法（教师点睛）。然后将数学方法反馈、应用于现实世界，创设新情境，提出新问题，如图1所示。最后教师设计问题进行测评以了解学生水平并针对不同层次学生给出个性化建议和指导。

不难看出，整个探究活动是一个循环的过程，也是一个由简单到复杂和由低级到高级的不断探索、应用、提高的过程。同时，也可以看出教师创设“好情境”、学生提出“好问题”是后面各阶段成功开展的前提，关系到后面各阶段的实施状况。

（一）  学习目标设置和学习者分析

要明确学生应学习哪些知识点，这些知识点要学习到何种层次。还要知道“学生已经知道了什么”，明确学生在知识和技能方面的起点，特别是思维和相关基本方法的掌握情况。同时要明确所面对的学习者群体的认知风格和个体差异的分布情况，为教学方案的设计提供指导。目标要易测量和评价，易决策设计。学习目标的描述可以是自然言语方式，也可以是稍显形式化的表征方式，如图2所示。横轴是知识类型，分为6类；纵轴是操作类型，“理解”“记忆”位于同一层次，属于低阶目标，对应于学习的意义建构阶段；“运用”位于高阶目标，对应于学习的能力生成阶段。

（二）  创设学习情境

情境能使学习者有机会生成问题、提出各种假设，并在解决结构不良的、真实的问题的过程中获取丰富的资源。同时，该情境还能提供其他丰富的例证或类似问题以使学习者产生概括化与迁移。数学情境是指数学概念、规律容易产生的现实背景和一种能促使学生主动的及自由的想象、思考、探索、解决或发现规律的环境、资源或者氛围，是广义的、宏观的大情境。有氛围，学生才有动力；有资源，才能去操作、去使用，才知道怎么去做。它呈现的方式可以是多媒体、虚拟环境、文字表述等。

在一个完整的教学过程中，教师需要先后创设以下三种学习情境。

1）问题情境。在学习中，学习新手首先看到一种问题情境，他们要先运用原有的知识去尝试理解情境中的现象和活动。问题情境相对较复杂，需要学生形成和解决一组相互联系的子问题，使学习者从多个侧面来审视情境中的每个问题。

创设问题情境的常用方法有：复习引导法、矛盾揭示法、激趣引疑法、以“误”引“悟”法和比较辨析法等。

创设问题情境的策略有：通过生产生活实际创设、通过相关学科的交叉点创设、通过幽默诙谐的悖论或故事创设、通过古典数学文化创设和通过数学实验创设等。

2）探究情境。教师引导学生将教学内容转化为学生认识的矛盾和内在的需要后，要依据学习目标和教学内容的核心观念，挖掘内在逻辑，营造一系列由表及里、由易到难、由近到远和逐渐深入的动态问题或活动内容，目的是搭建认知脚手架实现认知平台的跳跃或跨越，驱动学生深入理解核心观念背后所蕴含的知识与思想方法，达到对核心观念的理解与运用，进而提升数学关键能力。

创设探究情境的常用方法有：观察法、数形转换方法、归纳法、类比方法和分析法等。

创设探究情境的策略有：巧设悬念和疑点、观察、模仿、实验、猜想和反思等。

3）应用情境。对于知识和工具都只有使用它们，才能真正了解它们，数学理论应用化可培养数学运算、直观想象、数据分析、逻辑推理及分析和解决问题等素养。所以要创设应用情境，强化概念知识与事实知识在问题解决和任务完成过程中的运用。