机械优化设计课程案例引导式教学探究

摘  要：机械优化设计课程将最优化原理和计算科学相结合，课程内容理论化过强，严重制约着课程的教学效果。为此探索案例引导式的教学方式，以先导课程机械原理中的平面连杆机构运动综合为例，从学生熟知的内容出发以循序诱导的方式让学生理解优化的思想并学会建立优化模型，在课程内容理论讲授的同时，穿插基于Matlab软件的上机实验环节，以连杆机构的近似运动综合过程为牵引，由简入难，层层递进，逐步启发学生能够针对复杂机械工程问题建立数学模型，并学会选择和使用现代工具进行求解的能力。

关键词：优化设计；案例教学；引导教学；Matlab；优化模型

中图分类号：G642        文献标志码：A          文章编号：2096-000X（2023）11-0100-04

Abstract： The mechanical optimization design course combines optimization principles and computational science， and the course content is too theoretical， which seriously restricts the teaching effectiveness of the course. In order to explore the case guided teaching method， we take the motion synthesis of planar linkage mechanism in the pilot course Mechanical Principles as an example. Based on the content that students are familiar with， this study makes students understand the idea of optimization and learn to build optimization model in a step-by-step way. While teaching the theory of the course content， we interspersed the computer experiment based on Matlab software. We take the approximate motion synthesis process of connecting rod mechanism as the traction， and gradually inspire students to establish mathematical models for complex mechanical engineering problems， and learn to choose and use modern tools to solve them.

Keywords： optimal design; case study teaching; guided teaching; Matlab; optimization model

机械优化设计将机械工程中的设计问题转化为最优化问题，通过相应的优化算法进行求解，从满足要求的可行设计方案中搜寻得到最优设计方案。机械优化设计课程是机械类专业的专业技术课程，通过本门课程的学习，学生能够掌握机械优化设计的基本理论和基本方法，学会从工程实际问题中建立数学模型并对模型进行求解，初步具备利用所学机械优化设计的知识分析问题和解决问题的能力。优化设计是最优化原理和计算科学的结合，对数学基础有较高的要求，课程内容理论化过强，学生普遍具有畏难情绪，严重制约了课程的教学效果，因此很多学校选择在研究生阶段开设机械优化设计课程。

随着工程教育认证的开展，越来越多的学校和专业以OBE理念来设计人才培养体系，从专业培养目标的达成来制定毕业要求指标点，并将指标点分解后通过设置相应课程来进行支撑。基于其课程性质和课程内容，机械优化设计课程对毕业要求的指标点问题分析和使用现代工具能够形成有效地支撑，因此需要对该课程的教学进行改革，提高教学效果，有效达成设置的课程目标。现有的教学改革研究[1-3]多聚焦于教学内容的精选和简化、基于Matlab的实践性教学及研究性教学模式，对于教学方法的研究却很少。为了让学生更好地理解课程中抽象的概念和理论，案例式教学是一个有效的手段。现有的机械优化设计教材中均加入了大量的工程优化案例[4]，但是这些案例更多的是理论学习后的应用展示，缺乏对理论知识学习过程的引导，而且案例本身具有相当的难度，学生理解起来也有一定的困难。如何通过设置简单有效的案例来引导学生理解最优化的思想，能够建立优化模型，并使用现代软件进行优化求解成为亟待解决的问题。

一  优化思想的导入

（一）  机构运动综合的圆点和滑点

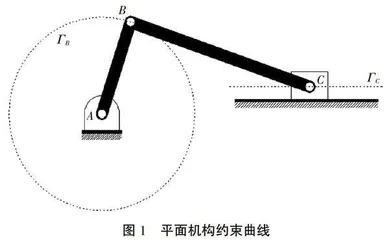
作为机械优化设计的先导课程之一，机械原理是研究机械的基本理论——机构学和机构动力学等问题的一门机械专业主干基础课，平面连杆机构运动综合是它的主要内容之一[5]。连杆机构的运动综合按照任务的不同可以分为位置综合、函数综合和轨迹综合，其中位置综合是确定连杆机构的尺寸参数，使得连杆可以引导刚体通过指定的若干位置。在机械原理的课程讲授中，通过对连杆机构的运动分析，将位置综合归结为在运动刚体上确定出圆点和滑点，其在固定坐标系中的离散轨迹点分别共圆（R-R二副杆的约束曲线）和直线（P-R二副杆的约束曲线），如图1所示。

接下来便可依据圆点和滑点的轨迹特征对其坐标进行解析求解。以圆点为例，假定其在刚体上运动坐标中的坐标为（xm，ym），通过坐标变换可以得到其在固定坐标系中离散轨迹点的坐标（xi，yi），i=1，2，…，n，若轨迹点所在圆的圆心在固定坐标系中的坐标为（xC，yC），半径为r，则可建立约束方程组，如下

上式方程组中方程的个数等于离散运动刚体给定的位置数n，即包含了n个代数方程，而未知量的个数为5。接下来可通过具体的算例引导学生分析该方程组的求解情况：当给定刚体的位置数少于5时，刚体上的圆点有无穷多个；当给定刚体的位置数恰好为5时，刚体上存在有限的圆点。根据选定的两个圆点及其对应圆心点的坐标便可确定所综合连杆机构的尺寸参数。最后向学生抛出思考题：当刚体的给定位置数超过5时，方程组无解，这时该如何确定圆点？

（二）  机构运动综合的近似圆点和滑点

当给定运动刚体更多的离散位置时，刚体上不存在轨迹点精确共圆和直线的圆点和滑点，这说明平面连杆机构无法引导刚体精确通过指定的多位置。这时，刚体上离散轨迹更接近于圆和直线的特征点——近似圆点和滑点便成为运动综合的搜寻点，其关键在于离散轨迹与直线或圆接近程度的评价。

对于平面离散运动刚体上任意点的离散轨迹点，可以选择不同（圆心坐标和半径）的圆或者不同（斜率和截距）的直线去逼近，如图2所示，在定义了逼近误差的描述函数后，这些圆/直线便有不同的逼近误差，其中逼近误差最小的圆/直线便是离散轨迹的最优逼近圆/直线，其逼近误差更能反映离散轨迹与圆/直线的整体接近程度。定义了最优逼近圆/直线后，刚体上不同的点便对应着不同的最优逼近圆/直线误差，误差取得极小值的点就是刚体上的近似圆点和滑点。因此，当给定刚体更多位置时，平面连杆机构的近似运动综合就是在确定了离散轨迹的最优逼近圆/直线后进行近似圆点和滑点的优化搜索。通过平面连杆机构少位置的精确运动综合到多位置的近似运动综合的过渡便向学生引入了优化的思想，如图3所示。

二  优化模型的建立

（一）  最优逼近圆/直线的优化模型

离散轨迹的最优逼近圆是通过对其所有逼近圆的逼近误差进行比较并选择最小误差得到的，逼近误差就是用来比较择优的统一标准，因而将逼近误差的描述函数称为优化的目标函数。目标函数可以根据实际的设计要求来设定，比如可以以所有离散轨迹点到逼近圆法向距离的平方和（最小二乘法）或者以所有点到逼近圆法向距离的最大值（最大误差最小法）作为目标函数。无论哪种具体的目标函数，均是以逼近圆的圆心坐标和半径为自变量，其也是优化对象的描述参数，因而称之为优化变量。逼近圆的圆心理论上可取为运动坐标系中的任意点，对圆心坐标没有任何限制，而对于半径，其取值必须大于零，从而将优化变量所需满足的条件称为约束条件。目标函数、优化变量和约束条件这三个要素一起便构成了离散轨迹最优逼近圆的优化模型。这样通过离散轨迹最优逼近圆的确定就初步让学生了解什么是优化模型，在此基础上对三个要素的内涵进行更深入地阐述，最后让学生写出最优逼近直线的优化模型，以此来考察学生是否掌握优化模型的建立，如式（2）所示，式中的两个优化模型分别对应着最大误差最小法和最小二乘法。

（二）  近似圆点/滑点的优化模型

对于刚体上近似圆点/滑点的优化搜索，目标函数为刚体上点的离散轨迹的最优近似圆/直线误差，优化变量为刚体上点的坐标，如式（3）所示，最优近似圆点误差优化模型，通过引导学生列出目标函数进而找到优化变量和约束条件这三个要素，半独立完成对近似圆点优化模型的创建，且通过引导学生对最优近似圆点误差优化模型进行创建，从而激发学生对建立优化模型的兴趣，使学生独立完成对最优近似滑点的优化模型创建，进一步加深学生对建立优化模型的理解和促进学习能力的提高。

对于约束条件则需要重点阐述，一方面可以让学生对机械原理课程中平面连杆机构的特性进行回顾并理解其在机构尺度综合中的约束作用，另一方面为后续的约束优化求解奠定基础。连杆机构的特性包括运动特性（曲柄存在条件）、急回特性以及传力特性，可以依此建立曲柄存在条件、最小传动角条件等约束方程。如图4所示，通过优化模型图流程图的建立，使学生对优化模型的创建过程可以有更直观认识，首先确立研究目标最优近似圆/直线优化模型，然后找出优化三要素：目标函数、优化变量和约束条件，最后通过优化三要素进行优化模型的建立。采取这种方式使困难的问题系统化，极大提高了学生学习的效率，并使其在生活和学习中更具系统性和流程性。

三  实践教学与教学回顾

（一）  基于Matlab的实践教学

优化模型的求解依赖于各种各样的优化算法，该部分内容需要有一定的数学基础支撑，往往在进行讲授的时候由于学生难以理解而无法达到较好的教学效果。对于本科生来说，能够选择和利用现有的工具对模型进行求解，便可以形成对毕业要求的支撑。对于数学模型求解Matlab是常用软件之一，且具有强大的数据处理、可视化功能。Matlab软件可以完美地充当求解工具的角色，学生无需根据优化算法编制相应的程序，仅需调用软件工具箱中的相关函数即可，这使得优化数学知识的讲解可以大大减少，从而降低了学习难度，还能提高学生解决实际问题的能力。因此在课程内容理论讲授的同时，穿插基于Matlab软件应用的上机实验环节。首先通过机构精确运动综合时约束方程的求解以及刚体平面上特征曲线——圆点曲线（三次代数曲线）和滑点曲线（圆曲线）的绘制，让学生掌握Matlab软件的基本语法、数值和符号计算及科学绘图等。然后以离散轨迹的最优逼近圆优化模型求解为例，让学生学会如何通过调用Matlab的优化工具箱函数来进行优化求解，最后让学生独立完成运动和传力特性要求下平面全铰链四杆机构的近似运动综合设计的优化模型建模及基于Matlab的优化求解。

图5为学生在理解少位置圆点优化思想的前提下，进一步独立完成最优逼近圆优化模型后，通过实践操作使用Matlab的优化工具箱实现数据可视化。通过数据可视化这种方式，使枯燥的理论知识具象化，从而提高学生的主观能动性，加深学生对机构综合设计的理解，并为后续的约束优化模型奠定基础。