新工科背景下高等数学课程教学改革探索

摘  要：高等数学是应用型本科院校各工科专业必修的一门基础课程，但由于种种原因，在实际教学中还难以达到新工科背景下对高等数学课程在人才培养过程中所提出的新要求。基于上述问题，对高等数学课程教学改革提出如下建议，结合学生实际和专业特点，整合和加工教学内容、强化数学思想方法的渗透。深化对知识的理解与应用、重视人文情感的渗透、凸显数学的育人功能、优化教学方式，拓宽学生参与度。

关键词：新工科;高等数学;培养策略

中图分类号：G642 文献标志码：A          文章编号：2096-000X（2022）21-0144-04

Abstract： Advanced Mathematics is a compulsory basic course for engineering majors in application-oriented universities. However， due to various reasons， it is still difficult to meet the new requirements of Advanced Mathematics course in the process of talent training under the background of new engineering disciplines in actual teaching. Based on the problems above， this paper puts forward the following suggestions for the teaching reform of Advanced Mathematics： combining with the students' reality and professional characteristics， integrating and processing the teaching content， and strengthening the infiltration of mathematical thinking methods， deepening the understanding and application of knowledge， paying attention to the penetration of humanistic emotion， highlighting the educational function of mathematics， optimizing teaching methods， and broadening students' participation.

Keywords： new engineering; Advanced Mathematics; training strategy

随着以互联网和工业智能为核心的新工科建设的推进，众多高校在探索和研究创新型人才培养模式的过程中，逐步认识到强化理工科基础教育是培养新工科人才的重要举措。目前，工科专业学习的高等数学主要是由微积分、空间解析几何、微分方程、向量代数与空间解析几何、无穷级数等内容组成。作为应用型本科院校各工科专业必修的一门基础课，高等数学课程的重要性不言而喻。但研究表明，包括高等数学课程在内的传统大学数学教学已不能满足新工科人才培养的需要[1]。

为了充分发挥高等数学课程在工科专业后继课程的基础与服务功能，促进工科生在更高层次和境界上进行创造性工作，提升高等数学课程的教学效果便尤为重要和急迫。课堂是教学活动的主要场所，课堂质量是教学质量的决定性因素。本文旨在结合作者多年来从事高等数学课程的教学经验，探索新工科背景下高等数学课程的教学改革，以提升其教学的有效性。

一、结合学生实际和专业特点、整合和加工教学内容

基于当前大部分工科高校高等数学课程内容多、学时紧的现实情况，如果按部就班地遵从教材安排，只要是教材里有的内容全部都教，往往会陷入匆忙赶进度、疲于教学的境地，难以取得理想的教学效果。为了保障学生在可接受的基础上，学习到相对完整的高等数学课程内容，顺利达成预期教学目标。教师不仅要考虑课程各部分知识内容的内在结构以及彼此之间的关联性，更需要考虑学生学习高等数学时的知识储备、现实需求以及后续专业发展特点，并以此为依据来整合加工教材内容。

首先，高等数学课程要做好与高中数学课程的衔接。高等数学是不少工科生在进入大学阶段后接触的第一门数学课程，因此教师有必要了解学生在高中阶段所学的数学内容及新课标对这些内容的相关要求。例如，包括导数、积分在内的微积分内容被纳入了高中数学教学体系，大学生已具备了一定的微积分知识和利用所学知识解决问题的能力。因此教师在高数课程的教学上要利用学生已有的微积分基础，对于现行高中和高数教材中重合的知识点如初等函数导数公式的推导、积分的性质等进行简单概述，重点让学生理解微积分背后所蕴含的数学思想以及追溯微积分产生的过程。学生在高中阶段仅对正弦、余弦、正切这三种三角函数有较深入的学习，教师在教学上要侧重于补充余切、正割、余割函数，并适当介绍和差化积公式、积化和差公式及半角公式、理解这些函数间的内在关系并能够进行函数间的灵活变形，为后续求导数、求积分奠定基础。

其次，高等数学课程要做好与学生所学专业的衔接。大学生学习的动机主要是学以致用，在于落实与行动。基于不少学生在高等数学课程的学习过程中常常会产生诸如“为何而学”“学有何用”的疑问，因此高等数学教学不能拘泥于数学，就数学而教数学，而需要邀请工科专业的相关领导与老师共同参与教学大纲的修订和课程的建设，把高等数学作为推动学生专业发展的杠杆，通过学科之间的交叉与融合，探究高等数学与学生所学专业之间的关联性、应用以及在学生后继学习和生活中的价值，以更好地支撑相应专业人才的培养目标。只有学生认识到这门学科的价值与应用后，才有学习的动力。目前不少工科专业采用的教材——《高等数学》（同济版）[2]，虽然很好地突出了数学的系统性与严密性，但仍难以顾及到工科不同专业的具体需求，使得工科专业高等数学教学出现了尽管存在专业差异，但课程内容几乎完全一致的问题。因此在教学中需要结合学生的专业特点，对教学内容进行有针对性的再处理和设计，突出这些知识点在学生专业发展过程中的作用。例如，利用微分方程模型来描述细菌的繁殖、疾病的发生规律，借助直线的投影、曲面立体（圆锥体）三视图等更好地进行工业制图、利用微分方程及傅里叶级数来学习信号系统课程等，尽可能体现新工科、新产业对高数内容及相应知识的需求变化。

二、强化数学思想方法的渗透，深化对知识的理解与应用

高等数学课程之所以成为众多工科专业学生必修的基础课程，不仅在于高等数学知识是工科生学习后续课程的基础，而且数学知识背后所蕴含的定量化、模型化思想都是精准解释和刻画所属专业中相关现象的工具，对学生后续的学习和发展具有重要作用。因此在教学中不能把重心全部着眼于现成结论的传授和训练，也要重视知识的发生过程和思维过程。例如，高等数学的精髓——微积分和解析几何的建立标志着数学由常量数学时期过渡到了变量数学时期，从此变量进入了数学、辩证法进入了数学，是数学发展史上里程碑式的大事件。其中，贯穿于微积分和解析几何中的变量思想、极限思想以及数形结合思想都有助于学生更好地理解充斥着变化的现实世界，而将实际问题转化为数学问题的过程，则在形成学生的数学抽象思维和数学建模能力方面具有重要作用。

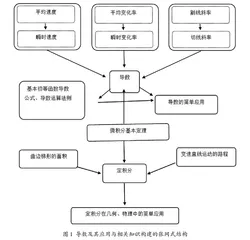
例如学习完某一章节的内容后，让学生用思维导图软件X-mind将孤立的、非结构化的零散知识点进行总结和梳理，能够避免学生在学习中只见树木不见森林的不足，有助于学生用整体的、联系的观点看待所学知识。如通过提炼极限、不定积分、定积分的求解方法，加深和巩固学生对所学知识的理解和掌握;通过导数及其应用与相关知识构建的张网式结构[3]（如图1所示）勾勒导数以及定积分产生的背景、相关应用以及彼此之间的联系，帮助学生理解导数的思想和内涵、感受导数在解决数学问题和实际问题中的作用。

三、重视人文情感的渗透，凸显数学的育人功能

新工科的内涵是以立德树人为引领，以应对变化、塑造未来为建设理念，以继承与创新、交叉与融合、协调与共享为主要途径，培养未来多元化、创新型卓越人才[4]。作为工科专业必修的一门基础课程，高等数学课程责无旁贷地承载着立德树人的根本任务，它在大学生形成正确人生观、价值观等方面具有独特作用。数学思想、精神、方法的运用反映出深蕴其中的文化价值，影响着人们的思维方式、智力发展、审美情趣、伦理道德[5]。因此，高等数学的教学不仅要注重知识的传授和习题的演练，还需要重视人文情感的渗透，凸显数学的育人功能。

（一）融入数学史内容，加深学生对课程内容的理解

在教学中穿插数学史内容，能够加深学生对相关概念和思想的起源及发展的理解。例如学生刚开始接触极限的ε-δ语言时难以理解和掌握，教师可适当介绍其相关历史。微积分诞生之初，虽在生产和实践中有广泛应用，但它的理论基础不够严密，表达不够严谨，因此英国的大主教贝克莱提出了所谓的贝克莱悖论。他认为“无穷小量”既等于0又不等于0，召之即来，挥之即去，这是荒谬的。究竟无穷小量是不是0，无穷小及其分析是否合理，由此引发了数学史上的第二次数学危机。此后，很多大数学家如阿贝尔、柯西、维尔斯特拉斯致力于分析的严格化。ε-δ语言让极限概念能用非常精确严格的数学语言给出描述，也为其他重要概念的严格化定义打下基础。比如，导数是函数增量与自变量增量比值的极限，定积分是一个特殊和式的极限，广义积分是普通定积分的极限，无穷级数是部分和数列的极限，这样学生就会对极限概念有了更深入的理解。

（二）强化审美教育，培养学生的审美鉴赏力

发现美、认识美以及对美的运用是人类生存的要求，而数学美则是发现美和塑造美的重要方法。英国哲学家罗素（Bertrand Russell）曾说：“数学拥有的不仅是真理，还有最极致的美。”因此，在抽象的高等数学内容中洞察数学的美，在教学中强化审美教育，培养学生的审美鉴赏力是提升教学有效性的重要措施。

除黄金分割比例、对称外，高等数学中很多立体图形因其独特而灵动的线条成为艺术家设计建筑物、艺术品时汲取灵感的重要来源之一。例如广州市重要的地标性建筑——广州塔因独特的螺旋曲线，被形象地称为“小蛮腰”，这一建筑运用的正是数学中的“单叶双曲面几何结构”。北京奥运会国家游泳中心“水立方”则是根据细胞排列形式和肥皂泡天然结构设计而成的，它的膜结构是世界之最，膜结构物则与微分几何中的极小曲面关系密切。因此，教师在教学过程中可以结合生活中熟悉的建筑物和艺术品来欣赏图形的美，并结合图形性质思考一些更深入的问题，这有助于工科大学生真正贴近现实生活，更好地学以致用。

同时，数学从混沌中找出秩序，将复杂还原为简单，追求简洁的表达方式本身就是一种独特的美学诠释方式。例如极限概念特别是现代的极限语言，很好地体现了有限与无限，近似和精确的辩证关系。牛顿-莱布尼兹公式不仅是沟通定积分和不定积分的桥梁，也简明扼要地描述了微分和积分这两种运算方式的联系和相互转化过程，在简约中隐含着深刻和含蓄。这些简洁和谐的数学公式和逻辑严谨的数学推理对培养学生运用数学眼光欣赏美和发现美具有重要作用。

（三）突出数学精神，重视高数在塑造学生性格中的作用

数学精神有助于个体品质和价值观念的形成，能够促进其精神成长[6]。因此，在高等数学教学中要深入挖掘隐含在数学知识背后的数学精神，让它能够鼓舞、激励大学生的成长。如在界定极限定义、微积分定义以及对数学问题进行求解和证明过程中有助于形成重证据、有条理、合乎逻辑的思维品质。而从1665年牛顿创造了“流数术”到1855年维尔斯特拉斯给出了极限的严格定义，整个极限概念逐步严格化的过程以及微积分的发现过程都可以感受到对事物的认识是需要一个过程的，不可能一步到位，有助于培养学生执着、坚韧、不惧怕困难、不屈服于挫折的勇气。

四、优化教学方式，拓宽学生参与度

大学生求知欲旺盛，具备较完备的知识结构和较强的学习能力，因此教师在教学中要回归学习的“引导者”和“帮助者”角色，提升学生的自主性和参与度，给学生更多的探索空间，力求改变“老师讲、学生听”的被动式教学。

（一）利用信息技术手段，加深学生对知识的理解

首先，信息技术手段能够将抽象内容形象化，有助于学生对知识内容的理解。相比高中数学内容，高等数学内容高度的抽象性和理论化使得不少学生望而却步。而信息技术则可以较好地弥补学生抽象思维、想象能力的不足，能够加深学生对知识内容的理解。例如定积分和重积分的概念本身非常抽象，如果不借助信息技术手段，教师无论将图像画得多细，都无法画出无限细分这一过程，学生理解起来很困难，而信息技术则能够直观地呈现这一动态过程，让学生清楚地看到每增加若干个点，小矩形的面积之和与曲线下的曲边梯形就更接近一些;每增加若干个小区域，平顶柱体的体积之和与曲面下面的整个曲顶柱体的体积就更接近一些，从而有助于学生对定积分和重积分概念的理解。