OBE理念下问题导向教学法探索

摘  要：工程教育专业认证背景下，高校各工科专业教师正在不断推进教育理念和教学方法改革。文章以画法几何与工程制图课程中垂直关系一节为例，开展问题导向式教学模式探索。改变线面关系传统教学中直接给出作图方法的单纯灌输知识的模式，通过问题引导推进课堂教学，鼓励学生探索，注重在解决问题的过程中学习理论知识，培养学生思考和解决问题的能力。采用分段融入三维建模的模式强化三维软件的工具属性，帮助学生在画法几何基础部分进行空间分析，提高学习兴趣、保持传统制图课程的系统性，也实现培养学生的自学能力和创新能力的教学目标。

关键词：问题导向;工程图学;三维建模;创新设计

中图分类号：G642       文献标志码：A          文章编号：2096-000X（2022）24-0124-04

Abstract： Engineering teachers in colleges are constantly promoting the reform of educational concepts and teaching methods under the background of the professional certification of engineering education. Taking the course of Descriptive Geometry and Engineering Drawing for example， the problem-oriented teaching model is explored in this paper， which differs from imparting knowledge  bysimply and directlygiving the diagram method in the traditional teaching mode. Through the question guidance to promote class teaching， encourage students to explore， and learn theoretical knowledge in the process of solving problems， students' ability to think and solve problems is cultivated. Moreover， the model of subsection incorporating 3D modeling is adopted to strengthen the tool attributes of 3D software to help students with spatial analysis in the basic part of descriptive geometry. It improves the learning interest， keeps the systematicness of the traditional drawing course， and achieves the teaching goal of cultivating students' self-study ability and innovation ability.

Keywords： problem-oriented; engineering drawing; 3D modeling; innovative design

工程教育专业认证遵循成果导向、以学生为中心、持续改进3个基本理念，对促进教学改革，提高工程教育人才培养质量至关重要。成果导向教育（Outcome-based Education， OBE）强调以学生的学习效果引导教学设计和教学方法[1]，要求学生具有解决复杂实际工程问题的能力。以工程制图课程为例，其作为工程教育的先导课程对学生能力的培养具有重要的作用[2]，教学目标在于使学生掌握工程图样的知识和技能，具备现代化设计人才所需的工程素养，并且随着信息化的发展，工程图学课程除了要分析解决教学遇到的传统问题，还需要不断吸收图学领域的新技术成果、拓展课程内涵[3]。在教学改革的过程中我们发现，一方面，学生在刚学习本课程时常常对用图形表达世界充满向往，但当课程渐入重点内容时却往往因为缺乏问题分析能力和空间想象能力产生畏难以及程式化套用现成定理的问题;另一方面，面对刻不容缓的BIM（Building Information Modeling）技术的教学应用[4]，学生确实有新鲜感，但是简单将三维建模的原理和技能整体融入教学的全过程，往往造成传统工程图学、二维计算机绘图和三维建模各部分的学习都缺乏系统性和连贯性，学生的注意力不断在三者之间跳跃，抓不住重点;而单独将三维建模内容设置在某一学期某一阶段，又会使得各部分之间的联系不够紧密，无法体现三者之间的关系。这些问题不仅造成学生在制图课程的学习效果上大打折扣，更使其在以后的工作中面对复杂工程问题时感到无从下手，从而与我国工程教育专业认证背景相悖，因此教学中应寻求新的教学方法着重培养学生的逻辑思维能力，以及分析解决问题的能力，并注重引入新技术的形式、时间和切入点。笔者在教学实践中提出了基于OBE的问题导向式教学法，由教师充当组织者和引导者，将每节课的知识点合理地设置于典型代表问题中，通过问题引导推进课堂教学，引导学生自主探索，使学生在不断地分析和解决问题的过程中自然而然地得到知识而非传统的结论灌输;同时采用分段融入三维建模的模式强化三维建模的工具属性，既提高了学习兴趣也保持了学习专注度，使学生的学习更具主动性，实现培养学生的自学能力和创新能力的教学目标。

本文以画法几何与工程制图课程中“直线与平面、两平面的相对位置”一章中“直线与平面垂直、两平面垂直”一节为例，根据问题导向式教学设计的五个环节，详细介绍教学组织的实施过程。

一、教学过程的组织和实施

（一）课前预习

1. 预习内容安排

课前预习在一定程度上确实能够提高课堂的学习效率，然而现代大学生课业压力大，可自由支配的时间越来越少。近年已成为高校教学改革重要方向的信息技术与传统教学深度融合的线上线下混合式的教学模式虽然大大提高了学生的参与度，但由于大部分引用该模式的课程采用的“线上自学、检验”和“线上复习、拓展”等环节均需要学生利用课下的时间来完成[5]，如果每门课程都采用类似的教学模式，可想而知，学生最终只会因为没有足够的时间而选择省去这些环节，而所剩的课堂面授环节，又由于教师只进行重点内容的解惑，最终导致学生整整一节课颗粒无收，教学效果甚至还不如过去的传统教学模式。因此，高校的课程改革应针对不同的课程合理采用适合的教学模式，而非简单的一刀切，使得教学效果从学生的角度达到整体最优解。长安大学画法几何与工程制图课程采用的问题导向式教学设计中本节课的课前预习环节并不是让学生花费大量时间去预习课堂内容，而是要求完成以下辅助任务：利用Revit三维建模在空间求一点K到已知平面P的距离。

2. 预习内容的可行性

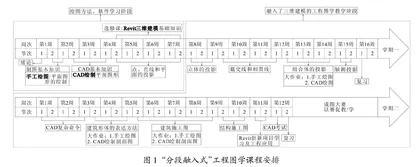
长安大学在2021年高水平教材修订项目中已将Revit三维建模引入了工程图学课程，采用“分段融入式”模型将教学过程分为两个阶段：第一个阶段是绘图软件学习阶段，第二阶段是融入了二维计算机绘图和三维建模的工程图学教学阶段。明确了课程以手工绘图和二维计算机绘图为主、三维建模为辅。三维建模是以选修课的形式被设置在二维计算机绘图之后，继而融入并贯穿于画图和读图的全过程，教学设计和安排仍然围绕传统图学投影理论，将课堂重点放在培养学生手工绘图能力上，从学生接受知识的角度进行合理的教学安排，使三维建模服务于二维，根据每节课知识点的不同，分别完成知识引入（立体的投影章节）、疑难解惑（截交线和相贯线章节）、结果验证（组合体的投影章节）和工程实践（建筑工程图章节）的四种工具作用，既保证了图学课程的完整性，又体现了三维建模和工程图学的有效融合。融入了Revit三维建模的画法几何与工程制图课程仍为110课时，其中第一学期62课时，讲到轴测投影，第二学期48课时，从建筑形体的表达方法开始讲起，具体的教学安排及时间节点如图1所示。根据三维建模选修课的设置时间安排，在本节课学习之前，学生已经学习了Revit三维建模的基本命令，可以在很短的时间轻松完成规定的预习任务，为接下来的教学面授环节做好准备。

（二）提出代表问题

本节课前学生已经掌握了点线面的基础知识，并学习了线面关系中的前两种关系：平行关系和相交关系，迫切需要通过对第三种关系——垂直关系的学习来解决复杂综合问题。本节课教学的重点为介绍垂直关系的投影特性及应用。以往的传统教学过程是直接给出此投影特性（若一直线垂直于一平面，则直线的水平投影必垂直于该平面内水平线的水平投影;直线的正面投影垂直于该平面内正平线的正面投影。反之则同样成立），接着举例进行固定方法应用，这种方式的弊端在于学生根本不用思考，只需被动接受定理和方法即可，不仅课堂枯燥，久而久之，这种机械性的记忆方式还会使学生在面对需要独立探索的复杂综合问题时却丧失了思考的能力。为了改变这种现状，笔者先是在开课前2分钟利用多媒体给大家展示我国古代到现代的代表性建筑，例如港珠澳大桥等（如图2所示），使学生惊叹于设计者高超技艺的同时，认识到垂直关系由于兼具安全上的稳定性和视觉上的美感，无论是在房屋建筑还是公路桥梁中都随处可见，进而围绕本节课的教学内容抛出与之有关的最直接的问题，即求距离问题。接着，用一个大家日常中的实例将该问题具体化，如：已知预留洞和楼板在设计图纸中的投影，如何得知洞中心到楼板的距离？为了寻找答案，将此实际问题简化为问题一：求点到平面的距离。最后，引导学生们带着这个代表问题一起开始此次课堂教学，产生对未知知识的求知欲。

（三）引导分析问题

让大家展示自己课前建立的模型，思考过已知点K如何能求得该点到已知△ABC所确定平面P的距离。通过学生的动手操作，很容易分析出应分为3个作图步骤：（1）过K点作平面P的垂线KM;（2）求垂足N;（3）求KN的实长。这个过程体现了三维建模在点线面基础部分帮助理解分析的工具属性，通过每节课针对不同知识点所采用的不同三维建模工具属性应用，不仅有利于图学课程内容的学习，也提高了学生的软件技能，使有意愿的学生可以顺利参加后续成图大赛，以赛促学、持续改进，增加就业的技能优势;同时由于该软件学习被安排在制图课程之外，也避免了对课程体系的影响。

根据现有知识学生只会前述作图步骤的后面两步，即利用线面交点法求垂足N和利用直角三角形法求KN的实长，需要解决的关键问题则是第1步过K点作平面P的垂线KM，从而引出思考——如何来保证在投影图中所做直线一定是平面的垂线？此时设置小组讨论环节，针对讨论结果一“使它垂直平面内两相交直线即可”引出讨论结果二“由于空间垂直两直线的投影一般不再垂直，因此不能仅由已知△ABC各边投影作出这条垂线”。问题到这里陷入胶着，考虑到想要突破一个新知识，我们往往是从已有的旧知识出发，于是老师可带领大家回顾并提问：在以往的学习内容中是否学过与垂直有关的内容？因为只有“直角定理”（当正交两直线之一平行于某投影面时，则它们在该投影面上的投影仍反映直角）这一个旧知识与垂直关系有关，因而学生很容易想到该定理，进一步激发出学生的求知欲，明白了想要利用直角定理，首先需要找到与平面有关的两条投影面平行线——水平线和正平线，就可以通过使这两条投影面平行线各自反映实长的投影分别垂直于已知直线KM的同名投影实现所做直线垂直该水平线和正平线，继而实现KM垂直于这两条相交直线（水平线和正平线）确定的平面P。而关于如何做平面内的投影面平行线，学生在前面内容中已经掌握，于是过K点作平面P的垂线KM这一步便已经实现，同时由于第二步和第三步都是旧知识，那么课前提出的问题一也便得到了解决，作图结果如图3所示。到这里学生已经跟随老师的思想完整分析并解决了一道典型的小综合题目，有了一点成就感，此时由老师趁热打铁，指出大家在解决该问题时的第一步作图过程其实就是我们本节课所要介绍的重要定理——垂直关系的投影特性（分析过程如图4所示），并强调利用该投影特性，我们不仅可以过已知点得到平面的垂线，还可以很方便地求解有关垂直关系的其他问题，同时举例说明。