安德森教育目标分类理论对中学数学教学的启示

摘  要：安德森教育目标分类理论是布卢姆教育目标分类理论的修订版本。该理论从“知识”和“认知过程”两个维度，分别分为4个类别、11个亚类和6个类别、19个亚类，对教学目标进行描述；表明了能力为不同知识在不同认知过程水平上的表现，对认知过程做了更细致的描述。在发展学生核心素养的教育大背景下，重温安德森教育目标分类理论，可以得到一些对中学数学教学的启示：精准定位教学目标，突出学习进阶过程，采用二维结构的评价框架。

关键词：中学数学；教育目标分类；学习评价；核心素养；水平划分

*

本文系喻平教授团队的“数学学习心理学研究及其教学启示”（中学）系列文章之十九。

当下，以发展学生核心素养为目标的课程改革正在推进。其中，将学业质量评价摆到了一个突出的位置。如何从对知识理解的评价转向知识理解与素养发展双重任务的评价，无疑是学业质量评价面临的新课题。学业质量评价历来是课程与教学论领域关注的问题。由于各个时代的教育目标不尽相同，学业质量评价的理论、方法、指标也就存在差异，甚至大相径庭。但是，历史上一些著名的教育评价理论都有其所长，某些理论对当前的课程改革具有一定的参考和借鉴价值。本文对安德森教育目标分类理论做回顾，剖析其对发展学生核心素养的中学数学教学的内在意义。

一、 安德森教育目标分类理论简述

（一） 基本框架

布卢姆在认知领域与情意领域对教育目标做了分类。在认知领域，分出6个类别：知识（对特定要素的回忆和识别）、领会（初步理解材料的意义）、应用（将抽象概念应用于特殊或一般的情境）、分析（将交流内容分解成各种组成要素或部分，以使有关概念层次清楚，或使概念间的联系表达清楚）、综合（把各种要素和组成部分组合成一个整体）、评价（为了特定目的对材料和方法的价值作出判断）。这6个类别的认知复杂性依次递增。每个类别的目标又基于因素，分为若干子目标，形成认知领域的教育目标体系。

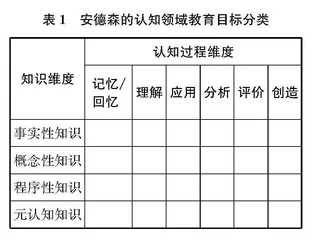
安德森等人于2001年对布卢姆的认知领域教育目标分类做了修订，把布卢姆体系中的“知识”作为一个独立的维度，分为四个类别：事实性知识、概念性知识、程序性知识、元认知知识。然后，用“记忆/回忆”替代布卢姆体系中的“知识”，将“领会”换为“理解”，将“综合”改为“创造”并放到“评价”之后。于是，就用一个二维体系来刻画知识维度与认知过程维度的关系（如表1所示）。［1］

此外，安德森还在知识维度下划分了11个亚类（如表2所示）［2］，在认知过程维度下划分了19个亚类（如下页表3所示）［3］。

根据表2和下页表3确定教学目标、设计教学活动和学习评价，并将有关内容填入表1对应的交叉格中。这个教育目标分类工具，使教师能够准确把握课堂教学目标，紧密围绕教学目标开展教学活动和学习评价。［4］

（二） 特征分析

1. 表明了能力为不同知识在不同认知过程水平上的表现

其实，布卢姆的教育目标分类也是对学习结果的一种水平划分，把学习结果分为6个水平。对这个线性序列的水平划分，可以理解为前面的“知识”“领会”“应用”是对知识掌握和理解的水平描述；后面的“分析”“综合”“评价”是对能力发展的水平描述。尽管这种解读比较牵强，特别是后面3个水平对能力的界定模糊不清，但是6个水平确实反映出了对学习进阶的刻画。

与布卢姆的体系不同，安德森修订的教育目标体系采用知识与认知过程两个维度进行分类。布卢姆所说的“知识”本质是对特定知识的回忆和识别，不是对知识本身的讨论，而安德森提出的“知识”是对知识本身的界定。安德森等人曾将知识分为陈述性知识和程序性知识。陈述性知识指知道事实、理论、事件是什么的知识；程序性知识指知道如何做某事的知识，既包括动作技能，也包括认知技能和认知策略。［5］这种广义的知识分类，事实上把能力作为知识看待。安德森认为，能力可以用陈述性知识和程序性知识的总量解释。安德森的教育目标分类理论中未出现“能力”这个术语，但是它的二维结构模型表明，能力为四类知识在不同认知过程水平上的表现，从知识记忆到运用知识进行创造，都是学生习得的能力的体现。［6］

在安德森的教育目标分类体系中，对于相同的知识类型来说，可以有多种不同的认知过程，因而可以形成不同的教学目标。同时，由于对知识做了分类，教师就可以根据知识的类型，设计不同的教学方法或策略；然后根据认知过程的记忆、理解、应用、分析、评价、创造等类别的不同加工程度和复杂性，设计不同的教学方法或策略。另一方面，安德森的教育目标分类理论事实上又是一个学习评价模型。与布卢姆的模型相比较，此二维结构模型直接将能力纳入评价范畴，涵盖了知识理解与掌握、能力发展两条主线，兼顾知识理解与掌握的进阶和能力发展的进阶，从而使评价结果更加精准。

2. 对认知过程做了更细致的描述

安德森对认知过程的6个类别及相关认知过程做了比布卢姆更加精准和细致的描述。以“理解”为例，用了7个词语进行刻画。7个词语的含义见表3，例子如下：（1） 解释，如把数字语言转化为文字语言；（2） 举例，如列举各种绘画艺术风格的例子；（3） 分类，如将观察到和描述过的精神疾病案例分类；（4） 总结，如书写录像带所反映的事件的简介；（5） 推断，如学习外语时从例子中推断语法规则；（6） 比较，如将历史事件与当代的情形进行比较；（7） 说明，如说明法国18世纪重要事件的原因。这种描述方式使“理解”这一概念的外延显得更加清晰，避开了空泛的词汇和模糊的概念，进而为教学及评价提供了可以具体操作的程序。

一个教学目标的陈述包括动词和名词。动词一般说明预期的认知过程，名词一般说明期望所获得或建构的知识。盛群力等人举了一个例子：学习者将学会区分政府体制中立法、司法和行政机构如何做到分工明确、各司其职。其中，“区分”属于认知过程中“分析”的一个具体类别（见表3）；“政府体制中立法、司法和行政机构如何做到分工明确、各司其职”为预期学习的知识类型提供了线索——“体制”是一个概念性知识。所以，根据表1，可以得出结论：这一目标落在“分析”和“概念性知识”相交的方格内。［7］也就是说，设计教学目标时，要对具体的内容做分析，从知识和认知过程两个维度来确定目标应当属于表1中的哪个方格，而这并不意味着所有方格都要有内容。

二、 对中学数学教学的启示

（一） 精准定位教学目标

安德森将教育目标分成知识和认知过程两个维度。在安德森的教育目标分类体系中，学生在认知领域习得的各种能力要用知识来解释，因而学生能力的发展依托于知识与认知过程的结合，两者结合才可以构成课程与教学的目标。现在，许多教师制定的教学目标中经常出现不够明确或显得空泛的目标，主要原因就在于没有很好地做到知识与认知过程的有机结合。具体分为两种情况：

第一种是，教学目标包含了具体的认知过程，但是没有与之相结合的知识，从而导致空泛。如“培养学生的数据分析能力”这个教学目标，主要涉及的认知过程是分析，但是在目标的叙述中，没有相对应的知识。学生需要分析什么样的数据？如何分析数据？用什么方法分析数据？这些问题使得实际的教学活动中目标无法落实，也就失去了意义。类似的目标还有“培养学生数形结合的能力”“发展学生的数学抽象、几何直观核心素养”等等。对于这种情况，如果在制定教学目标时加上知识的部分，则可使教学目标明确具体。例如，设计“诱导公式”的教学目标时，在“发展直观想象、逻辑推理素养”这一目标中加入具体知识，改为“从三角函数定义出发，借助单位圆关于原点的对称性，推导π＋α的正弦、余弦和正切，发展直观想象、逻辑推理素养”。这样，教学目标要求学生执行的认知过程仍然是分析，但是明确了具体的与认知过程结合的知识，如事实性知识（单位圆、原点）、概念性知识（三角函数定义）、程序性知识（推导π＋α的正弦、余弦和正切），也就明确了学生要学什么，教师要教什么，从而更容易落实。

第二种是，教学目标中只有具体知识，缺乏相关的认知过程，导致定位上的含糊。例如，高中数学中常见的教学目标设计“描述函数的概念”“叙述对数的运算性质”，从表述层面看是完整、规范的：其中“描述”“叙述”等学生行为是可观测、可检测的，此外也有“函数的概念”“对数的运算性质”等具体知识。但是，教学目标的实现可以是教师直接告知函数的概念，学生记住后描述出来；也可以是学生自主探究、合作讨论，在初中用变量的依赖关系描述函数的基础上，用集合语言和对应关系刻画函数，建立完整的函数概念。从表现上看，学生最后都描述出了函数的概念。但是，“描述”这一行为背后的认知过程是不同的：第一种只涉及“记忆”这一认知过程，也就是通过“记忆概念性知识”来实现教学目标；第二种则涉及理解函数“变量说”和使用数学语言刻画数学概念，该目标是通过“理解概念性知识”和“运用程序性知识”实现的，这种方式实现的是更高级的目标。［8］一个较为具体的教学目标可解释为两种不同的目标，是因为教学目标的设计中使用了表示行为的动词——描述，而没有明确表明认知过程，从而导致目标含糊。这也是安德森教育目标分类理论用“认知过程”取代“行为”的主要原因。

教师在综合考虑知识与认知过程来设计教学目标时，要明确教学目标中知识和认知过程分别属于哪个类别，从而精准设计教学目标，进而真正引导教学过程的开展。

（二） 突出学习进阶过程

学习进阶指“对学生在一个时间跨度内学习和探究某一主题时，依次进阶、逐级深化的思维方式的描述”［9］。学习进阶有五个组成要素：（1） 进阶终点，即最终学习目标；（2） 进阶维度，指学科内或科学实践过程中的核心概念；（3） 多个相互关联的成就水平，指反映学生思维发展过程的普遍阶段；（4） 各水平的预期表现，指处于特定理解水平的学生在完成某类任务时所应有的表现；（5） 特定的评测工具，指学习进阶包含的一套从开发、验证到使用的完整评估方法。［10］简单地说，学习进阶是指对知识理解的深化过程，这个深化过程需要由不同水平的状态来描述。

在安德森的教育目标分类理论中，记忆、理解是较简单的认知过程，运用、分析是中等程度的认知过程，评价、创造是较复杂的认知过程。事实上，这就为学生的学习进阶建构了一个水平划分的依据：记忆与理解对应低级认知水平，运用与分析对应中级认知水平，评价与创造对应高级认知水平。教师设计教学活动时，应注意突出学习进阶的过程。

例如，“等差数列与等比数列”的教学可以分为七步。第一步，让学生观察两组数列，探究每组数列的规律。第一组数列可以是：1，2，3，…，n-1，n；3，5，7，…，2n-1，2n+1；10，20，30，…，10（n-1），10n；a，2a，3a，…，（n-1）a，na；等等。第二组数列可以是：2，4，8，…，2n-1，2n；3，9，27，…，3n-1，3n；12，14，18，…，12n－1，12n；1，-1，1，-1，…，1，-1；等等。第二步，引导学生归纳两组数列的一般规律an+1－an=d（d为常数，n∈N*）和an+1an=q（q为常数，n∈N*），从而得到等差数列和等比数列的定义。第三步，引导学生推导等差数列与等比数列的通项公式。第四步，让学生应用通项公式解决一些简单的问题。比如：（1） 在公差为d的等差数列{an}中，已知a1=-1，d=4，求a8；已知a1=9，d=2，an=-15，求n。（2） 在公比为q的等比数列{an}中，已知a1=1，q=2，an=16，求n；已知q=-32，a4=-27，求a1。第五步，引导学生迁移应用等差数列和等比数列的通项公式、求和公式等知识，解决一些现实问题和跨学科问题。第六步，引入差比数列概念：如果数列{an}满足an+1=Aan+B（其中A、B为常数，A≠0，n∈N*），那么称数列{an}为差比数列。显然，当A=1时，{an}是等差数列；当B=0，{an}是等比数列。这样，将两种数列统一在一个式子中，建立两种数列的联系。第七步，引导学生迁移应用两类数列知识背后的思想方法，发现一些新知识，解决一些综合性问题。比如，经典的二阶等差数列问题：“在平面上画n条直线，假设其中任意2条直线都相交，且任意3条直线不共点。设这n条直线将平面分成了an个部分，写出数列{an}的递推公式和通项公式。”