大概念引领下的数学教学境脉创设
作者: 杜海燕 吕增锋
摘 要:作为“问题(任务)链”的基础,“境脉”是“情境”与“脉络”的合并,即通过整体把握知识的相关情境,以一定的脉络串联整个课堂教学的情境,从而有效化解传统教学情境创设的弊端。大概念统摄、关联、迁移的本质特征能为境脉的搭建提供有利的线索与依据。在数学教学中,可以大概念为认知基点把握境脉,以大概念为知识节点规划境脉,最终,以大概念为思维生长点设计境脉。
关键词:高中数学;大概念;情境;境脉;平面向量基本定理
虽然“核心素养是通过情境的实践发展起来的”[1]观点已经成为共识,但在实际教学中,情境的创设普遍存在形式单一、内容碎片化以及为情境而情境等问题。于是,学术界提出了“境脉”的概念。顾名思义,就是“情境”与“脉络”的合并[2],即通过整体把握知识的相关情境,以一定的脉络串联整个课堂教学的情境,从而有效化解传统教学情境创设的弊端。因为情境通常是问题(任务)的背景,所以,“境脉”通常是“问题(任务)链”[3]的基础。
那么,情境的脉络如何搭建?这就离不开大概念的支持。大概念又称学科大观念,是指从学科内容中抽象概括出来的具有广泛联系整合作用并能够广泛迁移应用的概念或观点[4]。它处于学科的中心位置,对学科其他内容具有统摄力、关联性,集中反映学科的本质,体现学科的思想方法(也即学科专家的思维方式),凸显学科的价值,兼具认识论、方法论和价值论三重意义。[5]大概念统摄、关联、迁移的本质特征能为境脉的搭建提供有利的线索与依据。下面以“平面向量基本定理”为例,谈谈笔者对此的看法。
一、境脉的把握:以大概念为认知基点
境脉的创设不是“无本之木、无源之水”,首先需要解决的是知识的本原性问题,即对学习内容的充分理解和本质把握。这就要求教师对学习内容有全面、深刻(关联性、统摄性)的认知。大概念源于学科中的各种概念、原理以及解释体系,是知识和技能的抽象与提炼,是思想方法的整合,是核心素养的表征,是学生在遗忘大部分细节后仍然能保留下来的重要理解。[6]毫不夸张地说,大概念就是学习内容的高度凝练。因此,以大概念为认知基点,有助于教师扩大对学习内容认知的视域,提升对学习内容认知的高度。
很多教师对平面向量基本定理缺乏全面而深刻的认知。比如,只知道平面中任意的向量都能够用两个不共线的向量来表示,平面向量基本定理为平面向量(乃至平面上的点)的坐标表示做了铺垫。对此,可以大概念为认知基点来丰富、深化认识。首先,思考“学什么”的大概念。平面向量基本定理本质上就是向量的线性运算,是由“向量是一种运算”这一大概念衍生出来的。其次,思考“为什么学”的大概念。“平面中任意的向量都能够用两个不共线的向量来表示”背后体现的是“用有限来表示无限”这一大概念。扩大视域来看,“用有限来表示无限”是自然的选择,比如,红、黄、蓝三种颜色构成所有的色彩,物质几乎都是由原子、分子、离子构成的,动植物都是由细胞构成的等。“用有限来表示无限”也是人类的生活追求,比如,用若干尺码来表示所有衣服的大小,用若干面值来表示所有货币的金额,用7个音符来表示所有的乐曲,用26个字母来组成所有的单词,用不多的笔画来组成各种汉字。“用有限来表示无限”更是数学发展的基本诉求,比如,用10个阿拉伯数字来表示所有的数,用锐角三角函数来表示任意角三角函数,用圆心和半径两个要素来表示任意圆等,甚至哥德巴赫猜想、四色定理等著名数学难题研究的也是“用有限来表示无限”。感悟这两个大概念是“平面向量基本定理”重要的教学目标,或者说育人价值。因此,应该围绕这两个大概念创设“平面向量基本定理”教学的境脉。
二、境脉的规划:以大概念为知识节点
数学有着严谨的逻辑结构体系,由于这个体系比较抽象和枯燥,很难让学生理解和掌握。这就需要通过创设境脉,促使学生认知结构中的有关知识建立起实质性的和非人为的联系,从而将知识的逻辑结构转化为认知的发展(生长)脉络。大概念居于学科中心,具有超越当下和自身的持久价值和迁移价值。因此,大概念可以作为建立知识之间联系的关键节点,通过打破数学知识的原有边界,实现对数学知识的优化重组,从而打造出一个联系紧密的教学境脉。
平面向量基本定理的发现与验证是教学的重难点。通常的做法是,创设“力的分解”物理情境,通过类比联想得到平面向量基本定理。但是,这样做实际上并不严密。首先,“力的分解”往往指向正交分解,而平面向量基本定理指向的是任意分解;其次,由“力的分解”很难说明平面向量基本定理中参数λ1与λ2的存在性与唯一性。也就是说,单凭“力的分解”这个情境,很难让学生体验到平面向量基本定理发现与验证的完整过程。因此,教学中应该以“向量是一种运算”“用有限来表示无限”这两个大概念为节点,立足平面向量基本定理的发现与验证,创设多个相互关联的情境,形成一个完整的境脉。在“发现”环节,创设现实情境与数学情境,分别让学生体会“用有限表示无限”是自然的选择、生活的追求与数学的诉求,从而认识定理的价值;在“验证”环节,创设数学实验情境和数学运算情境,分别让学生体会“向量作为线性运算”的几何意义与运算性质,从而验证定理的存在性、唯一性、任意性。
三、境脉的设计:以大概念为思维生长点
依循境脉中隐含的知识脉络,期望学生可以像学科专家那样去发现问题、解决问题,实现知识的“再创造”。专家思维的一个重要特征就是,其调动的认知结构中的知识是靠大概念组织起来的——这反映的是学科专家对学科理解的广度与深度。因此,以大概念为思维生长点来创设境脉,可以把学习内容、学习环境、学习条件、学习者自身状态等构成境脉的诸多要素有机地融合在一起,从而让学习者获得更有意义的学习体验。
以“向量是一种运算”“用有限来表示无限”这两个大概念为思维生长点,可以创设如下引导学生发现与验证平面向量基本定理的境脉:
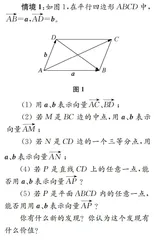
情境1:如图1,在平行四边形ABCD中,AB=a,AD=b。
(1)用a、b表示向量AC、BD;
(2)若M是BC边的中点,用a、b表示向量AM;
(3)若N是CD边的一个三等分点,用a、b表示向量AN;
(4)若P是直线CD上的任意一点,能否用a、b表示向量AP?
(5)若P是平面ABCD内的任意一点,能否用用a、b表示向量AP?
你有什么新的发现?你认为这个发现有什么价值?
情境2:公元前500年左右,希腊出现了一位哲学家,名叫德谟克利特。他是首个对自然界万物的构成提出假想的人。他提出任何事物都是由无限不可分割的“原子”构成。随着对微观世界的了解,发现原子的世界居然别有洞天!原子可再分:原子由原子核和在其周围的电子构成,原子核由质子和中子构成,质子和中子由夸克构成。目前研究发现,夸克是不可再分的粒子。原来夸克才是躲在原子核里的羞姑娘,夸克和电子才是构成物质的基本。
“用有限表示无限”是自然界的选择,你还能举出其他的例子吗?
情境3:鞋码,通常也称鞋号,是表示鞋大小和肥瘦的一种标志。它是一个地区、一个国家脚型特点和脚型规律的反映。世界各国采用的鞋码标准并不一致,但一般都包含长、宽两个测量量。长是指穿者脚的长度,而且一般都设置约12个不同的尺码来满足所有正常人的需求,例如表1所示的欧美男鞋鞋码标准。
“用有限表示无限”也是生活的追求,你还能举出其他的例子吗?
情境4:请在白纸上,以直尺和笔为工具,验证“平面中任意一个向量都能用两个不共
线的向量来表示”这一结论。请设计实验方案,并说明实验的合理性与科学性。
情境5:能否利用几何画板或GeoGebra来进一步验证你的猜想。
情境6:对于a=λ1e1+λ2e2,如何借助运算来确认λ1、λ2的唯一性?如果改变e1、e2的
方向,平面中的任意向量a还能够用e1、e2表示吗?如何通过运算来证明?
情境7:在平行四边形ABCD中,AB=a,AD=b。
(1)若P是线段BD上的一个动点,用a、b表示向量AP;
(2)若P是线段BD外的一个动点,用a、b表示向量AP。
你有什么新的发现?能否利用向量运算来验证?
情境1是数学情境,改编自人教A版高中数学教材中的例题。经过之前向量线性运算(加法、减法和数乘)的学习,学生已具备解决第(1)、第(2)问的经验。通过从特殊到一般的问题设计,引导学生独立思考、大胆猜想,初步感知、发现“对于平面中三个共起点的向量,其中一个向量能够用另外两个向量来表示”这一结论,展现学生对平面向量基本定理最朴素的理解。通过对定理价值的思考,初步体悟“用有限来表示无限”的数学思想。
情境2和情境3分别是科学情境和生活情境,意在让学生体会“用有限来表示无限”的自然意义和生活价值,感受数学与现实的联系,深度激发平面向量基本定理的学习动机。
情境4和情境5是数学(实验)情境,意在通过实验操作,引导学生认识到平面向量基本定理的运算背景是平行四边形法则,物理背景是力的分解,并促使学生将“平面中任意一个向量都能够用两个不共线的向量来表示”抽象为“a=λ1e1+λ2e2”,从而将对定理的认识从模糊的感性上升到明晰的理性。
情境6和情境7是数学(运算)情境。前者引导学生通过合作学习,对平面向量基本定理的存在性、唯一性、任意性进行严格证明,展现数学推理的严谨性,让学生感悟“向量是一种运算”这一大概念。后者组织学生探究平面向量共线定理,经历从特殊到一般再到特殊的专家思维过程,感受平面向量基本定理在研究平面位置关系中的作用。
实践哲学认识论有一个重要的观点:当认识用于指导人们的实践时,需要经历一个再情境化、再具体化的过程。在这个过程中,境脉不但贯穿始终,而且实现了飞跃式发展。因此,境脉的创设不是一成不变的,而要在大概念的引领下不断地“进化”,从而为后续学习的开展奠定基础。
参考文献:
[1]钟启泉.基于核心素养的课程发展:挑战与课题[J].全球教育展望,2016(1):3-25.
[2]黎加厚.创感时代的境脉思维[J].中国现代教育装备,2009(10):3-4.
[3]唐恒钧,张维忠.数学问题链教学的内涵与特征[J].教育研究与评论(中学教育教学),2021(1):8-12.
[4]华志远.落实“大概念”教学理念——对高中数学新教材中三角函数定义变更的思考与教学[J].教育研究与评论(中学教育教学),2021(1):72-75.
[5]马燕青,吕增锋.围绕学科大概念备好数学课[J].教育研究与评论(中学教育教学),2022(3):27-30.
[6]宗德柱.大概念教学的意义、困境与实现路径[J].当代教育科学,2019(5):25-28.