“寻本求变”:数学微专题复习课设计
作者: 支耀红
摘 要:设计数学微专题复习课,可以采用“寻本求变”的方法:寻找教材中代表一小类问题的基本题,对其进行适当的变式,以形成一组题目。针对初中数学考试中常见的有关“十字架”结构的平面几何问题,设计微专题复习课:从教材中以正方形为背景的简单题目出发,设计开放问题,引导学生探索能够得到三角形全等的各种其他条件;进而变正方形为其他常见图形,并适当改变条件或所求,引导学生从寻找到构造得到有关的三角形全等或相似,从简单到复杂解决问题,从而充分挖掘问题本质,发现解题规律。
关键词:初中数学;微专题复习课;教材题;变式
一、 数学微专题复习课设计可“寻本求变”
一般来说,中考数学一轮复习根据知识模块(“大单元”)划分课时内容,进行知识点“拉网式”复习,帮助学生夯实知识基础,完善认知结构;二轮复习根据常考题型(大类的问题,如开放性问题、新定义问题、阅读理解问题、情境应用问题等)或解题策略(高位的思想方法,如分类讨论、转化化归、数形结合、整体处理等)划分课时内容,进行解题的专题式教学,帮助学生感悟试题特点,体会解题思维。在此基础上,为了进一步提升备考复习的针对性,近年来流行起微专题复习课:相比于二轮复习课,进一步聚焦“结构相近”的一小类问题展开解题教学,帮助学生充分挖掘问题本质(通性),发现解题规律(通法)。[1]
因此,设计微专题复习课关键是,针对考情适当选取代表一小类问题的典型题目。对此,可以采用“寻本求变”的方法。一方面,教材中的例题和习题都是专家精心选择的经典问题,很多中考试题都是在教材题的基础上加工、改编、拓展、综合而产生的,“寻本”就是寻找教材中代表一小类问题的基本题。另一方面,因为是代表“一小类”问题的题目,所以相互之间会存在比较清晰的变式关系,“求变”就是对教材中的基本题进行适当的变式(包括加工、改编、拓展、综合等),以形成一组题目。由此,可以很好地体现这一小类问题的“变与不变”(内部结构),以促进学生的解题迁移(举一反三);同时,可以遵循循序渐进的原则,让前面题目的解答为后面题目的解答作出铺垫,有利于贴近学生思维的“最近发展区”展开解题探索,让学生充分体会到解法是如何想到的以及还可以怎样变化(包括优化)。
二、 《常见图形中的“十字架”结构》一课的“寻本求变”设计
近些年初中数学各级各类考试中,常见有关三角形、四边形中“十字架”结构的平面几何问题:在这类问题的图形中,出现了分别过三角形或四边形相邻两个顶点向相邻两条对边上的点引的两条线段,它们交叉形成了一个“十字架”(这是一种基本图形)。这时,借助三角形或四边形中已有的边或角相等,加上一些其他条件,便可以得到有关的三角形全等或相似(这是解决这类问题的关键步骤),进而得到更多结论以解决问题。针对这一小类问题,笔者尝试设计一节微专题复习课。
翻阅苏科版初中数学教材,笔者发现,八年级下册第9章《中心对称图形——平行四边形》复习题第19题第(1)小题的图形中,出现了正方形中的“十字架”结构。因为正方形邻边相等,邻角相等且互补,所以,正方形中“十字架”结构的有关结论最强(最特殊),也最容易发现。于是,笔者从该题出发,设计开放问题,引导学生探索能够得到三角形全等的各种其他条件;进而变正方形为其他常见图形,并且适当改变(包括增加)条件或所求,引导学生从寻找到构造得到有关的三角形全等或相似,从简单到复杂解决问题,从而充分挖掘问题本质(识别基本图形),发现解题规律(抓住关键步骤)。具体题目及其教学意图如下:
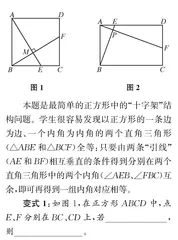
教材题:在正方形ABCD中,如图1,如果点E、F分别在BC、CD上,且AE⊥BF,垂足为M,那么AE与BF相等吗?证明你的结论。
本题是最简单的正方形中的“十字架”结构问题。学生很容易发现以正方形的一条边为边、一个内角为内角的两个直角三角形(△ABE和△BCF)全等:只要由两条“引线”(AE和BF)相互垂直的条件得到分别在两个直角三角形中的两个内角(∠AEB、∠FBC)互余,即可再得到一组内角对应相等。
变式1:如图1,在正方形ABCD中,点E、F分别在BC、CD上,若 ,则 。
变式2:如图2,在矩形ABCD中,点E、F分别在AD、CD上,若BE⊥AF于点P,则BE与AF相等吗?
变式1对正方形中的“十字架”结构做开放设问,引导学生围绕两个三角形全等,梳理条件和结论的对应关系。学生不难发现,再添加任意一组边对应相等(如AE=BF或BE=CF)或一组内角对应相等(如∠AEB=∠BFC或∠EAB=∠FBC)的条件,都可以得到两个三角形全等,进而得到其他边或内角对应相等以及AE⊥BF的结论。由此可对正方形中的“十字架”结构有更全面、深入的认识。
变式2变正方形为矩形,并且变向下、向右的两条“引线”为向右、向上的两条“引线”,让学生探究其中的“十字架”结构。一方面,引导学生发现随着正方形变为矩形,邻边不再对应相等,邻角依然对应相等,三角形全等变为三角形相似;另一方面,引导学生发现“十字架”结构形成的关键除了两条“引线”出发的两个顶点相邻,还有两条“引线”终止的两条对边相邻。由此,学生拓展了对“十字架”结构的认识。
变式3:如图3,在正方形ABCD中,点E、F分别在AD、CD上,AE=DF,BE与AF相交于点P。若四边形DEPF的面积是1,PA的长为1,则正方形边长等于 。
变式4:如图4,在矩形ABCD中,AB=4,AD=6。点E、F分别在AD、CD上,且AE=2,DF=3,BE与AF相交于点P。若PQ是△BFP的中线,则PQ的长等于 。
变式3在正方形中“十字架”结构的基础上,增加有关图形面积与线段长的条件,要求正方形的边长,从而提升了题目的综合性,能够让学生更好地体会到“十字架”结构作为基本图形的运用价值。由“十字架”结构得到Rt△ABE≌Rt△DAF后,学生不难发现,四边形DEPF和Rt△ABP分别是全等的两个三角形去掉重叠部分后的剩余部分,因此它们的面积相等。于是,利用Rt△ABP的面积和PA的长,很容易求出PB的长……
变式4以两组直角边对应成比例的方式给出矩形中的“十字架”结构,在此基础上增加有关三角形中线的条件,要求该中线的长度,同样提升了题目的综合性,能够让学生更好地体会到“十字架”结构作为基本图形的运用价值。由“十字架”结构得到BE⊥AF后,学生可以利用已知的Rt△ABE和Rt△DAF的直角边长,逐步求出Rt△BFP的斜边长……
变式5:如图5,在等边△ABC中,点E、F分别在AC、BC上,AF与BE相交于点P。若AE=CF,则AF、BE互相垂直吗?
变式5变正方形为正三角形,让学生探究其中的“十字架”结构。重点引导学生发现:随着正方形变为正三角形,邻边和邻角依然对应相等,三角形依然全等,但是两条“引线”的夹角不再是90°,而变成60°。由此,学生进一步拓展了对“十字架”结构的认识:两条“引线”的夹角不固定,而与全等或相似的两个三角形中对应相等的已知多边形(常见为三角形和四边形)的两个邻角有关。
变式6:如图6,在菱形ABCD中,点E、F分别在AD、CD上,AF与BE相交于点P。若∠AEB=∠AFD,求证:AF=BE。
变式6变正方形为菱形,并且给出一组角对应相等的条件,让学生探究其中的“十字架”结构。重点引导学生发现:随着正方形变为菱形,邻角不再对应相等,已有的三角形既不全等也不相似了;但是,邻边依然对应相等,因此,可以尝试构造三角形全等。由此引导学生发散联想,得到构造三角形全等的方法:(1) 抓住邻边相等,作等腰三角形来构造,如图7(作BG=BA,可得△BGE≌△ADF)或图8(作AG=AD,可得△AGF≌△BAE);(2) 抓住给出的一组角对应相等,作等腰三角形来构造,如图9(作BG=BE,可得△BAG≌△ADF)或图10(作AG=AF,可得△ADG≌△BAE);(3) 想到菱形高相等,作直角三角形来构造,如图11(作BG⊥AD于G,AH⊥CD于H,可得△EGB≌△FHA)。由此,学生可以认识到:解决“十字架”结构的问题,关键步骤“寻找三角形全等”有时也是难点所在,因为需要作辅助线“无中生有”地构造。
变式7:如图12,在四边形ABCD中,∠ABC=∠D=90°,AB=3,AD=5,CD=25,点E、F分别在AD、CD上,AF与BE相交于点P。若AF⊥BE,求BEAF的值。
变式7进一步变正方形为更具有一般性的四边形,让学生探究其中的“十字架”结构。这里的四边形有一组对角均为90°,实际上就是图2中的四边形DEPF或CBPF。本题如
果直接让学生解决,则思维含量较高,颇有难度。但是,有前面的问题带来的对“十字架”结构的认识做铺垫,结合四边形的一组对角均为90°以及两条“引线”相互垂直,学生就比较容易想到,过点B向AD、CD作垂线,从而构造稍有变化的矩形中的“十字架”结构(如图13所示)。由此,便可得到Rt△GBE∽Rt△DAF,进而得到BEAF=BGAD,从而将目标转化为求BG的长。这时,可以通过追问或提示,引导学生发现四边形ABCD的三边已知,一组对角均为90°,可以连接对角线(AC),两次利用勾股定理,求出第四条边的长(BC=6);并且发现在点B处,已知的∠ABC为90°,构造的∠GBH也为90°,可以得到Rt△GBA∽Rt△HBC,进而得到BGBH=BABC=12。接着,便可引导学生设BG=x,BH=2x,然后利用矩形对边相等,得到AG=2x-5,CH=25-x,最终在Rt△GBA或Rt△HBC中利用勾股定理,求得x=2+255……这样,便通过一个比较难的问题,让学生认识到“十字架”结构问题更多的可能性以及“构造三角形相似”作为关键步骤的处理技巧和运用价值。
参考文献:
[1] 李庾南,刘东升.初中数学复习课的细分与教学[J].教育研究与评论(中学教育教学),2024(3):4750.