高三复习要保持一定的思维张力

摘 要：高三二轮复习期间，一道立体几何测试题的考查结果不理想，讲评过程存在问题。为了提高教学效益，高三复习必须保持一定的思维张力，以不断培养学生的思维能力。为此，要在精心选择题目的基础上，精心设计教学过程，发挥题目应有的教育价值，尤其要激励学生正视困难，引导学生突破化解；鼓励学生多向思考，促进学生联系比较。

关键词：高中数学；高三复习；立体几何；解题教学；思维能力

一、 一道立体几何测试题的讲评

高三二轮复习期间，我市举行了一次中档题专项测试，其中一道立体几何题如下：

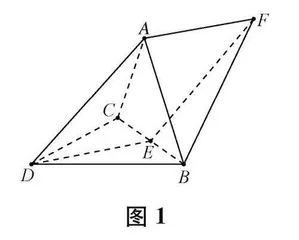
如图1，在三棱锥A-BCD中，DA=DB=DC，BD⊥CD ，∠ADB=ADC=60°，E为BC 的中点。

（1） 证明：BC⊥DA；

（2） 空间一点F使得四边形ADEF是平行四边形，求二面角D-AB-F的正弦值。

这道题改编自2023年高考数学新课标Ⅱ卷第20题，满分12分。某校A班学生的均分仅为6.28分，远低于该校的均分。

按理说，经过一轮复习，一道中档的立体几何题不应该成为学生的障碍。是什么原因导致测试结果不理想呢？

我调阅了A班学生的答题卡，发现所有学生解第一问用的都是综合几何法，解第二问用的都是空间向量坐标法。解第二问时，以D为原点建系的学生很多，却无一人沿着这条路走到底；其他学生都以E为原点建系，但是其中不少人因为种种原因未能走到底，只有少数人完全做对。

班级整体测试结果不理想，通常都不只是学生的问题，还与教师（之前）的教学有关。为了了解教师的教学情况，我又到该校听了A班数学老师的试卷讲评课。该题的讲评过程大致如下：

教师读题后，先请一位学生板演第一问的解答过程：

（1）因为E为BC 中点，DB=DC，所以DE⊥BC（记为①）。

因为DA=DB=DC，∠ADB=∠ADC=60° ，所以△ABD与△ACD均为等边三角形，所以AC=AB，从而连接AE可得AE⊥BC（记为②）。

由①②，且AE∩DE=E，AE、DE平面ADE，所以BC⊥ 平面ADE。

而AD平面ADE，所以BC⊥DA。

教师打对号评价后总结：对于立体几何解答题，一般地，第一问用综合几何法，第二问用空间坐标法。

然后问学生：第二小题应该怎么建系？学生作出图2后回答：以D为原点，建立如图所示的空间直角坐标系。教师点评：这样建系没有充分利用题目中隐含的三条直线两两垂直的信息，最好以E为原点建系。

带领学生证明DE⊥AE后，教师投影标准答案的解答过程：

（2） 不妨设DA=DB=DC=2，则AB=AC=2，故△DBC≌△ABC。

因为BD⊥CD，所以AB⊥AC，并且BC=22，DE=AE=2。

所以DE2+AE2=AD2，所以DE⊥AE。

又因为DE⊥BC、AE⊥BC，于是以E为原点，ED、EB、EA所在直线分别为x、y、z轴，建立如图3所示的空间直角坐标系，

则E（0，0，0）、D（2，0，0）、B（0，2，0）、A（0，0，2）。又因为四边形ADEF是平行四边形，所以F（-2，0，2）。

设平面DAB与平面ABF的一个法向量分别为n1=（x1，y1，z1）、n2=（x2，y2，z2），由n1·AD=0，n1·AB=0得2x1-2z1=0，2y1-2z1=0，取x1=1得n1=（1，1，1）。由n2·AB=0，n2·AF=0得2y2-2z2=0，-2x2=0，取y2=1得n2=（0，1，1）。

设二面角D-AB-F的平面角为θ，则cosθ=n1·n2/n1·n2=2/3×2=6/3，所以sinθ=3/3。

停顿片刻后，教师总结：有了空间坐标法之后，立体几何题相当于计算题，只需要按部就班地运算，确保无误即可。

二、 对高三复习教学的启示

这道题的讲评，引发了我对高三复习教学的思考。数学是思维的体操，数学教学要培养学生的思维能力，这是数学教育工作者的共识。然而，笔者看到的现状是：不少教师认为，培养思维能力是新授教学的事，高三复习时间紧、任务重，只需要多练题、多讲题。实际上，如果不从根本上提升学生的思维水平，则无法应对常变常新的高考发展要求——尤其是在从知识立意转向能力和素养立意的高考改革背景下，反套路、反机械刷题已成为共识，新颖别致的试题层出不穷。因此，为了提高教学效益，高三复习必须始终保持一定的思维张力，即让学生多做有思维含量的事，把学生的思维调动起来，使其处于一种适度紧张的状态。

显然，保持思维张力，要精心选择例题和习题，将选题的落脚点放在是否有助于学生思维的展开，能否发展学生思维的深刻性、灵活性、批判性和创造性上。在此基础上，还要精心设计教学过程，发挥题目应有的教育价值。尤其要做好以下两点：

（一） 激励正视困难，引导突破化解

保持思维张力，不能片面追求抓牢基础，让学生反复做简单题——不少地方存在这样的“应试”做法。对于较难的题目，要激励学生正视困难，不轻易放弃，进而引导学生积极探索，深入思考，或者迎难而上正面突破，或者另寻他途迂回化解，从而克服困难解决问题，从中增强意志品质（解题信心与毅力），磨炼思维品质（解题思想与智慧）。为此，首先要尊重学生的想法，理解学生的思路，从而准确把握学生在解题过程中遇到的困难。

上述测试题A班学生的均分不高，说明这道题对他们而言是普遍存在困难的。分析学生的答题情况和课堂表现可以发现，学生的困难具有一定的共性，主要在于怎样合理地建系，建系后如何写出相关点的坐标。

很多学生抓住BD⊥CD这一特征，以图2所示的方式建系。这种建系方式有一定的合理性，我们要尊重学生的这一想法。这时，学生的困难在于无法求出点A和点F的坐标。课堂观察发现，教师是清楚学生在此处存在困难的，可惜他轻易地滑过了这一学情，强行拉到图3所示的建系方式下。事实上，即便以图3所示的方式建系，仍然有不少学生无法求出点F的坐标。课堂中，教师呈现了标准答案供学生记录，却忽略了隐藏在答案背后的学生困惑。

面对这一困难，我们既可以引导学生正面突破，也可以引导学生迂回化解。当然，即便是迂回化解，也应是在尝试正面突破后作出的理性选择。

首先是正面突破。以图2所示的方式建系，怎样求出点A的坐标呢？它不像B、C等点的坐标可以简单地观察或向坐标轴投影直接得到。我们可以引导学生分析点A的几何特征，借助于方程思想间接地求出它的坐标。不妨令DA=DB=DC=2，设A（x，y，z），可以由长度条件AB=AC=AD=2得x2+y2+z2=4，（x-2）2+y2+z2=4，x2+（y-2）2+z2=4，据此得A（1，1，2）；也可由角度条件∠ADB=60°得cos∠ADB=DA·DB/DA·DB=2x/2×2=1/2，据此得x=1，同理得y=1，再由长度条件DA=2得x2+y2+z2=4，据此得z=2。经历了求点A坐标的过程，学生迁移相关的方法与经验，求点F的坐标自然不在话下：可以由ADEF是平行四边形得DF=DA+DE=DA+1/2（DB+DC），进而得DF（即点F）的坐标——这里其实融入了向量基底法的思想。

其次是迂回化解。在学生感受到以图2所示的方式建系求点A和点F坐标时陷入复杂的数式运算后，我们可以追问：为什么这样建系？还有没有其他建系方式？如何选择更合理的建系方式？事实上，学生以图2所示的方式建系，说明他们潜意识里已经发觉利用BD⊥CD这一条件能够使一些点落在轴上或轴面内，这是降维思想的萌芽。上述追问可以引发学生的关注，引导学生将无意识的行为转化为有意识的思考，将直觉的判断转化为理性的选择，将模糊的认识升华为清晰的策略。学生最终选择以图3所示的方式建系解决问题后，教师可以通过更多的例题帮助学生充分认识到：选择坐标系时，要充分利用已有的垂直关系，尽量让更多的点落在轴上或轴面内，从而优化解题的运算过程。可选取的例题如：

1. （2016年高考数学全国乙理科卷）如图4，在以A、B、C、D、E、F为顶点的五面体中，面ABEF为正方形，AF=2FD，∠AFD=90°，且二面角D-AF-E与二面角C-BE-F都是60°。

（1） 求证：平面ABEF⊥平面EFDC；

（2） 求二面角E-BC-A的余弦值。

对于本题的第二问，注意到平面ABEF⊥平面EFDC，因此，最好让z轴落在平面EFDC（x、y轴落在平面ABEF）中， 进一步考虑让点C或D落在z轴上。这样，可以过点C或D作EF的垂线（垂足为G），过点G在平面ABEF内作EF的垂线GH，以G为原点 ，GE、GH、GC（或GD）所在直线为x、y、z轴，建立空间直角坐标系。由此，题中各点的坐标都容易表示，后续的计算便不成为困难。

2. （2017年高考数学浙江卷）如图5，已知四棱锥P-ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，点E为PD的中点。

（1）证明：CE∥平面PAB；

（2）求CE与平面PBC所成角的正弦值。

本题中蕴含着很多垂直关系，但是，到底怎样建系更容易计算大有讲究。过点B作BO⊥AD于O，以O为原点建立空间直角坐标系，这时点P恰好在轴面内。设BC=1，不难表示出图中所有点的坐标，下面就一马平川了。

（二） 鼓励多向思考，促进联系比较

保持思维张力，不能片面追求熟练度，让学生大量做题。对于精选的例题，要舍得花时间，让学生从不同的角度，运用不同的思维方法去解决。在多向思考中，学生势必要广泛地运用到有关的概念、公式、定理等，从而汇聚不同部分的知识，密切各个板块的联系，这对于发展思维、培养综合运用知识与方法的能力无疑大有裨益。在多向思考中，还可以引导学生反思解题过程、比较解题方法，归纳发现问题本质、感悟解题通法，进而优化解题思维，提升思维品质。

立体几何是发展学生直观想象、逻辑推理、数学运算等核心素养的绝佳载体，历来是高考重点考查的内容。对于立体几何解答题，一般有综合几何和空间坐标两种基本的解题方法。综合几何法对于直观想象、逻辑推理能力有较高的要求，而空间坐标法操作流程固定清晰，思维含量相对较低，因此，在实际应用中更受到师生的青睐。那么，是不是有了空间坐标法，综合几何法就可以退出数学的舞台了呢？我们要辩证地看待这个问题。

首先需要指出，即使不考虑空间坐标法本身是算法思想凝结的思维之花，也不考虑数学运算本质上属于逻辑推理这种思维活动，而只从顺利解题的功利视角出发，空间坐标法也并非如某些师生认为的只需要“无脑”地运算，其中充满着思维的成分，尤其是需要思考如何建系：建系方式不同，解题（运算）繁简迥异。例如上述迂回化解过程。

此外，一方面，空间坐标法相较于综合几何法，往往运算量比较大，稍有不慎，就前功尽弃；另一方面，空间坐标法虽然套路固定清晰，但是也将很多数学内涵隐藏在运算中，不利于学生感悟蕴含于问题中的数学本质。

对于上述测试题，如果注意到DE⊥平面ABC，所以FA⊥平面ABC，不难发现平面FAB⊥平面ABC，即二面角F-AB-C为直二面角；而二面角D-AB-F可以分解为二面角D-AB-C和二面角F-AB-C，故要求二面角D-AB-F的大小，关键是求二面角D-AB-C。具体地，如图6，过点D作DG⊥AB于G，过点G作GH∥AF，交BF于H，连接GE，易知∠DGH为二面角D-AB-F的平面角，∠DGE为二面角D-AB-C的平面角，∠HGE为二面角F-AB-C的平面角，等于90°，所以sin∠DGH=sin（∠DGE+90°）=cos∠DGE=GE/DG=3/3。

相对于空间坐标法，该解法简捷明快，不仅运算量小，更能让学生体验到思维的乐趣，而且能够揭示这道题的本质：在三棱锥A-BCD中，求二面角D-AB-C的大小。这是立体几何的基本问题，不难利用三垂线法作出其平面角来求解。这种感悟到问题本质的深层理趣是空间坐标法所无法给予的。

A班所有学生第一问都用综合法，第二问都用坐标法。如此整齐划一，想来与教师过分强调、过度驯化不无关系。综合法和坐标法无所谓优劣，各擅胜场，因题而异，因人而异。让学生通过反思比较，迅速判断并作出选择，这也是需要培养的思维能力。

另外，需要说明的是，坐标法只是向量法的特殊状态。教学中，教师不应将向量法窄化为坐标法，而应让学生充分地感受到向量法的灵活性（可以任意选定基底）及其基本想法（将向量用选定的基底线性表示，即求各基底向量前的系数）与坐标法（求各维度的坐标）的一致性。

具体到上述测试题，提供的条件强烈地暗示可以DB、DC、DA 作为基底来解决（这三个向量大小相等、两两的夹角已知）。过程如下：

（1） 设DB=e1，DC=e2，DA=e3，则e1=e2=e3=2，e1·e2=0，e1·e3=e2·e3=2，则BC=DC-DB=e2-e1，所以BC·DA=（e2-e1）·e3=0，所以BC⊥DA。

（2） 设平面DAB的一个法向量为n1=ue1+ve2+we3，则由n1·DA=0，n1·DB=0 得e1·（ue1+ve2+we3）=0，e3·（ue1+ve2+we3）=0，取u=1得n1=e1+3e2-2e3。类似地，由AF=DE=1/2（e1+e2），AB=DB-DA=e1-e3，可得平面ABF的一个法向量为n2=e2-e3。据此，不难求得二面角D-AB-F的平面角的正弦值为3/3。

处理立体几何解答题，在强调学生掌握空间坐标法的同时，也不应关闭其他方法的大门。我们应该引导学生“既爱康庄的大道，也爱泥泞的小路”。事实上，那种罕有人至的小路更能培养学生的思维能力和数学素养，而只能按既定的路线行走的人注定是没有批判性与创造力的平庸者。

*本文系江苏省教育科学“十三五”规划课题“指向高中生数学关键能力的解题教学实践研究”（编号：D/2020/02/220）的阶段性研究成果。