守正创新：把准数学高考的育人导向

摘 要：2024年高考数学全国卷严格依标命题，努力守正创新。一方面，秉承以往全国卷的一贯风格，关注社会生活，挖掘数学史料，守学科育人的正确目标；全面覆盖基础知识，突出考查主干内容，着力考查通性通法，守学生发展的正确基点；指向本质，多思少算，守数学思维的正确路径。另一方面，贯彻党的二十大精神，服务选才，创有效甄别的新结构；考查能力，创深化思考的智力游戏、知识交汇、新型定义等新情境；聚焦素养，创推进教改的新契机。

关键词：数学高考；全国卷；思维能力；数学素养；守正创新

2024年，教育部教育考试院命制了3套（4份）高考数学全国卷：全国甲卷（文、理科）、新课标Ⅰ卷、新课标Ⅱ卷。这3套试卷既同根共源、一脉相承，又相对独立、各具特色。本文将从整体视角进行分析探讨，以期让大家更生动地感知数学新高考的改革脉搏，更深刻地理解数学新高考的命题立意，更准确地把握高中数学的教学关键。

2024年高考数学全国卷严格依标命题，努力守正创新，坚决落实立德树人根本任务，深入考查“四层”“四翼”，突出考查思维能力与数学素养，很好地发挥了人才选拔功能，引导数学教学深刻反思，把准数学高考的育人导向。

一、 守正：守正确目标，守正确基点，守正确路径

2024年高考数学全国卷秉承以往全国卷的一贯风格，简约大气、清新自然、内涵隽永，体现了守正的特点。

（一） 立德树人，守学科育人的正确目标

1. 关注社会生活，树数学实践价值

2024年高考数学全国卷命题坚持思想性与科学性的高度统一，围绕我国社会经济发展与学生个人发展，积极探索情境的人文性、趣味性、新颖性、生活性［1］，命制具有教育意义的试题，引导学生热爱社会、热爱生活，树立正确的人生观、价值观、世界观。如：全国甲卷（理科）第17题创设了工业产品质量的现实情境；新课标Ⅰ卷第9题创设了农村农业收入的现实情境；新课标Ⅱ卷第4题创设了水稻亩产量的现实情境，第18题创设了体育比赛的现实情境。

2. 挖掘数学史料，蕴数学文化内涵

数学史料是人类文明的智慧结晶，也是高考命题的鲜活素材。2024年高考数学全国卷命题巧妙地嵌入数学发展历程中的经典模型与活动，引导学生感受数学的真、善、美，极大地提升了试题的文化内涵与品味。如：新课标Ⅰ卷第7题融入了斐波那契数列的变形，第11题融入了笛卡儿叶形线，第14题融入了“田忌赛马”模型的变形，第17题融入了鳖臑模型的组合；新课标Ⅱ卷第16题融入了幻方游戏，第19题融入了帕斯卡定理。

（二） 深化基础，守学生发展的正确基点

2024年高考数学全国卷依据课程标准规定的学业质量标准，围绕数学内容主线，聚焦学生对重要数学概念、定理、方法、思想的理解和应用，深化基础性考查，强调对知识的本质理解、对方法的真懂真会，引导教学从机械“刷题”、盲目钻研套路向素养培养转变，为学生终身学习与发展奠定坚实基础。

1. 全面覆盖基础知识

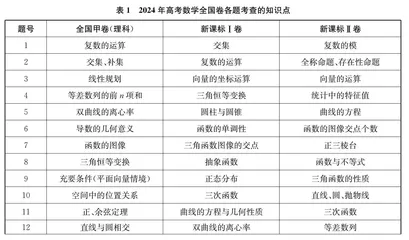
单从一份全国卷看，高考数学命题可能不能完全做到知识覆盖，但是从整体上看3套全国卷，可以发现知识之间相互补充，做到了对高中数学知识的全覆盖，引导教学不要猜题押题，必须依标施教。试题遵循“低起点、缓坡度、高落差”的原则，降低初始题起点、增加基础题题量，让学生较好地适应高考氛围，较快地进入考试状态，体现命题的人文关怀。各题考查的知识点（甲卷未统计选考题）如表1所示。

2. 突出考查主干内容

新课标卷、全国甲卷的考查内容分别按照新、旧课程标准的知识范围设定，特别是全国甲卷的文科试卷，回避了排列组合、空间向量等课程标准知识范围外的内容，对支撑学科知识体系的主干知识保持很高的考查比例，使之成为试卷的主体，并达到必要的深度。［2］2024年高考数学全国卷除去集合、简易逻辑、复数、线性规划等知识之外，对函数与导数、三角函数、数列、立体几何、解析几何、统计与概率等6大版块的主干知识进行了重点考查。新课标Ⅰ卷中，主干知识共考查130分，占比86.7%；新课标Ⅱ卷中，主干知识共考查135分，占比90%；新高考甲卷（理科）中，主干知识共考查120分（未统计选考题），占比85.7%。主干内容重点考，引导中学教学以课程目标为指引，注重知识的基础性和方法的普适性，避免随意深挖。

3. 着力考查通性通法

2024年高考数学全国卷得到全国师生以及专家的广泛好评，其中一个重要原因就是，每道试题都将对通性通法的考查有机融入数学知识，深入考查基本原理与基本思想方法，淡化特殊技巧，没有偏题、怪题、“套路题”、“秒杀题”，有效检测学生对知识中蕴含的思想方法的理解与掌握程度，真正达到了考查能力素养的目的。

例1 （2024年高考数学新课标Ⅰ卷第8题）已知函数f（x）的定义域为R，f（x）＞f（x-1）+f（x-2），且当x＜3时，f（x）=x，则下列结论中一定正确的是（  ）

A. f（10）＞100

B. f（20）＞1000

C. f（10）＜1000

D. f（20）＜10000

本题以斐波那契数列为背景，将“等”改为“不等”，创设数学学习新情境，深度考查学生的推理能力。解答本题，不是机械套用斐波那契数列的性质，而是回归研究递推数列的基本方法，逐项分析f（3）＞3，f（4）＞5，f（5）＞8，…，f（10）＞89。本题在考查基本运算的同时，巧妙考查逻辑推理：注意到f（3）没有上限，可排除C、D；又因为A不一定正确，所以选B。

可以看到，解答本题无法套用任何现成的模式，也没有可直接利用的已知模型。这正体现了高考数学命题突出考查学生分析问题和解决问题的能力，引导中学教学回归基础、减少“刷题”的决心与能力。

例2 （2024年高考数学新课标Ⅰ卷第11题）造型“”可以做成美丽的丝带，将其看作下页图1中曲线C的一部分。已知C过坐标原点O，且C上的点满足横坐标大于-2，到点F（2，0）

的距离与到定直线x=a（a＜0）的距离之积为4，则（  ）

A. a=-2

B. 点（22，0）在C上

C. C在第一象限的点的纵坐标的最大值为1

D. 当点（x0，y0）在C上时，y0≤4x0+2

本题以笛卡儿叶形线为背景，创设数学探究情境，让学生经历平面曲线研究的完整过程，考查学生对解析几何学科本质的理解，考查学生知识网络的完整性与系统性。

本题设计的四个选项环环相扣，层层递进。首先根据原点到点F（2，0）的距离与到定直线x=a（a＜0）的距离之积为4求出a=-2，或者直接检验a=-2正确，由此得到曲线C的方程为（x+2）（x-2）2+y2=4（x＞-2）。该方程与平常所学的圆锥曲线方程相比显得复杂，非常考验学生的心理素质。此时应该对照目标分析C、D选项。本题故意设置成D选项比C选项容易，考查学生现场应变能力。曲线方程变形为y2=16（x+2）2-（x-2）2，化等为不等，得到y2≤16（x+2）2，易判断D正确。又因为A、B都正确，所以C不需要再考虑。如果直接研究C选项，首先要发现曲线C经过点（2，1），如此，问题转化为研究曲线C在x=2处的导数是否为0，构造函数进而研究导数即可。当然，也可以考虑用特殊值法：当x=32时，y2=6449-14=207196＞1，故C错误。

可以看到，本题完全没有现成套路，就是原原本本考查学生分析问题、解决问题的能力。而且，本题求解方法多，入口宽，思维要求逐步抬高，突出考查了特殊与一般、转化与化归、函数与方程等数学思想方法。本题的巧妙之处更在于破除学生对解析几何问题的固有认识，回归解析几何的本来面目，通过选项的优化设计，有效控制计算量，避免繁难运算，实现了对思维能力的考查，有效选拔拔尖创新人才。

（三） 立足本质，守数学思维的正确路径

2024年高考数学全国卷注重考查知识的本质与知识之间的内在关联，考查学生对概念、原理的深入理解和灵活应用；同时加强思维考查，突出考查思维过程、思维方法。这引导数学教学“慢下来”，要注重知识的自然生成与螺旋建构，由此培养学生从源头思考问题的习惯、研究问题时求优求简的能力。

1. 概念、原理指向本质

2024年高考数学全国卷强调对概念、原理的深入理解和综合应用，考查知识之间的内在联系，引导学生重视对学科理论本质属性和相互关联的深刻理解与掌握。如：全国甲卷（理科）第5题考查双曲线的定义，第10题考查空间中的位置关系原理，第13题考查二项式系数概念；新课标Ⅰ卷第6题考查函数的单调性原理，第9题考查正态分布概念，第12题考查双曲线的定义，第18题第（2）问考查函数的中心对称原理；新课标Ⅱ卷第4题考查中位数、极差、平均数等概念，第7题考查正棱台概念，第16题考查极小值原理。

例3 （2024年高考数学新课标Ⅱ卷第7题）已知正三棱台ABC-A1B1C1的体积为523，AB=6，A1B1=2，则A1A与平面ABC所成角的正切值为（  ）

A. 12

B. 1

C. 2

D. 3

本题以正三棱台为载体，依托台体的体积与空间中直线与平面所成的角考查学生的直观想象、数学运算、逻辑推理素养。如图2，通过台体的体积公式求出台体的高，进而在台体的特征梯形中求得A1A与平面ABC所成角的正切值。如图3，将台体补形为锥体，将问题转化为在三角形中求解，运算大大简化。

2. 明算理算法，多思少算

2024年高考数学全国卷明显传递“多思少算”的考查理念：很多试题都可以较大程度地避免繁难运算，给学生充分思考的空间，突出考查学生的思维品质；在控制计算量的同时，加大思维量，特别注重思维考查的层次性。如新课标Ⅰ卷、Ⅱ卷的第15题，两道题模型一致，都是由两块三角板拼接而成的；如果能结合图形的特征，添加辅助线，化斜为直，则可以避免大量复杂的计算。又如新课标Ⅰ卷的第17题，立体几何解答题，如果能用综合法，作出二面角的平面角，结合平面几何知识，则可以很便捷地求解。

例4 （2024年高考数学新课标Ⅰ卷第16题）已知A（0，3）和P3，32为椭圆C：x2a2+y2b2=1（a＞b＞0）上两点。

（1） 求C的离心率；

（2） 若过P的直线l交C于另一点B，且△ABP的面积为9，求l的方程。

本题创新问题呈现方式，看似平淡，实质考查思维水平，不同解法下的计算量大相径庭，能达到很好的甄别区分效果。具体来看，不同的解题路径如图4所示。

路径1“直译”条件，思维量最小，运算量最大，耗时最长；路径2采用分割法求三角形的面积，与路径1相比，计算AD的过程得到简化；路径3重新构图，抓住S△APB=9，将问题转化为研究点B的轨迹方程，使运算大大优化；路径4深度挖掘图形的几何特征，根据S△APO=92，发现隐藏在数量关系背后的对称性，运算量微乎其微。

二、 创新：创新结构，创新情境，创新契机

2024年高考数学全国卷贯彻党的二十大精神，积极创新试题设计，持续深化考试内容改革，服务拔尖创新人才选拔，助推素质教育发展，助力教育强国建设。

（一） 服务选才，创有效甄别的新结构

2024年高考数学新课标Ⅰ卷、Ⅱ卷将原来的22道题减少为19道，其中多选题、填空题、解答题各减少1道。解答题的总分值由原来的70分增加为77分，其中第18、19两题均设置3个问题，分值都为17分。题量减少意味着学生的思考时间增加，可以更专注、更深入地思考，更从容地试错；也说明进一步强化了对思维过程与思维能力的考查，让优秀的学生能够充分发挥、脱颖而出。